QUESTION:
QUESTION:
Earth rotates on its axis and makes a full 360 degree turn in ~24hrs, so ~ 460 m/sec- if this is the case then if one jumps off the ground for even a split second (kids do all the time) then why does the ground underneath not shift?
 ANSWER:
ANSWER:
The simple answer is that the jumper has a horizontal
velocity equal to that of the earth and therefore moves forward right in
pace with the ground. The complicated answer is that Newton's laws are not
valid in a rotating frame of reference, so you do not land exactly where you
jumped from. There is a "fictitious
force" called the
Coriolis force which causes an object propelled straight up to not
continue straight up and straight back down.

 QUESTION:
QUESTION:
If a particle accelerator machine (like the LHC) was designed to be able to discharge the fast moving particles directly into the atmosphere (after they reached high speed), would observers be able to see, hear or feel anything?
 ANSWER:
ANSWER:
If the beam was sufficiently energetic and intense, air
molecules would be ionized and would subsequently radiate light. You would
probably not hear or feel anything.
 QUESTION:
QUESTION:
Let's say we have planet A and B. Planet A suddenly fly away from planet B at 1/2 the speed of light. Planet B also suddenly fly away from Planet A at a little bit more than 1/2 the speed of light. If we observe from Planet A, we can see Planet B because light travelled from Planet B to Planet A. However, after all the flyings, Planet A and Planet B will be 'separating' from each other at a little bit faster than the speed of light. Does it mean that after a while, observers from Planet A can no longer see Planet B? How does this workkkkk???????? :(
 ANSWER:
ANSWER:
For clarity, let us have a third planet D relative to which
your experiment happens. So the speed of A relative to D is vA=0.5c
and the speed of B relative to D is vB=0.6c let's
say. Your assumption is that the speed of A relative to B is 1.1c. (c
is the speed of light); that is wrong. In an
earlier answer I discussed this kind of problem. The speed
v with
which A and B each see the other going away is given by
v=(vA+vB)/[1+(vAvB/c2)]=1.1c/[1+(0.5x0.6c2/c2)]=0.85c.
Not intuitive, but true!
 QUESTION:
QUESTION:
How can a stationary radio receiver set to a particular frequency receive transmissions from a moving transmitter, say, from an aircraft?
Why doesn't the movement of the aircraft cause its radio transmission to be off frequency relative to the static receiver?
 ANSWER:
ANSWER:
As is also the case for sound waves, the Doppler effect is
not noticeable if the speed of the source is very small compared to the speed
of the waves. Someone walking toward you and talking does not sound like
Mickey Mouse; the receiver here is your ear and it is not sensitive enough
to detect the shift. The expression for the shifted frequency f of
electromagnetic waves relative to the source frequency f0
is given by f=f0√[(1+β)/(1-β)] where
β=v/c
and v is the speed of the source and c=3x108
m/s is the speed of light; β>0 is when velocity is toward you.
If β is much smaller than
1, it may be shown that the fractional change in frequency is |f-f0|/f0≈β.
For example, suppose the source is an airplane with speed 300 m/s (about 700
mph) and the frequency is 90 MHz. Then |f-f0|/f0≈10-6
or the Doppler shift is |f-f0|≈90 Hz. A tuner does not
have nearly the sensitivity to detect a 10-4% change in
frequency.
 QUESTION:
QUESTION:
If a gun was fired at the escape velocity of the Earth in a direction that it would not hit anything but not straightly up but instead more like in an angle of 45 degrees would the round still go to space? And if not what would the velocity needed be for a round that is fired at 45 degrees in to the sky be in order for the round to escape Earth?
 ANSWER:
ANSWER:
First, let's be clear that we are talking about an ideal
situation where we neglect the effects of air drag (which will slow the
projectile) or earth's rotation (which can add or subtract from the velocity
you give the projectile). The easiest way to get the value of the escape
velocity (ve) is to use energy conservation. Escape
velocity is that velocity which results in the projectile being at rest at
r=∞. Taking the potential energy U(r)=-GMm/r+C
to be zero at r=∞ (i.e., choose C=0), energy
conservation gives �mve2-GMm/R=0
where M and R are the mass and radius of the earth,
respectively; so, ve=√(2MG/R). You will
notice that this derivation has been done without any reference to the
direction of the velocity ve, so the direction
makes no difference.
 QUESTION:
QUESTION:
The famous "twins paradox" where each twin sees the other's clock running slower --- but then, when the rocket-twin returns to earth, she finds in reality that it was her clock actually running slower, I know that the answer to this riddle is that the effects of relativity are only happening when the rocket ship is travelling in a straight line at constant speed -- and not during the periods of acceleration or deceleration. But I still don't get it. What's happening during those periods of acceleration? For example, when the rocket ship first starts out, it is accelerating; What's actually happening regarding the aging of the twins during this phase?
 ANSWER:
ANSWER:
I really do not think you understand the twin paradox very
well; you should go to the FAQ page either here
or here. To understand what is
going on, nothing need be said about the periods of acceleration; maybe that
is what you meant. When you ask about "�what's actually happening�", it
depends on who is measuring elapsed time. On the ship, time passes normally
when the ship moves with constant velocity but if you accelerate, it is like
being in a gravitational field (equivalence principle) so you would observe
clocks to slow down relative to when your velocity was constant. For an
observer watching the ship, time runs slower compared to the observer's clock
when the velocity is constant; when accelerating, there is instantaneously a
normal time dilation due to the velocity at that instant.
 QUESTION:
QUESTION:
in a charged conductor electric field inside it is zero but in a non
conducting charged object it is not so why
 ANSWER:
ANSWER:
The most important property of a conductor is that some of
the electrons in it are free to move. If you try to put an electric field
inside a conductor, the electrons will move and they will keep moving until
they exactly cancel out the original field. In a nonconducting material,
electrons cannot move and so if you put an electric field on it the
electrons may move a little but they cannot move enough to nullify the
original field. This applies to electrostatics; there can be a field inside
a conductor when charges are moving, for example a current-carrying wire.
 QUESTION:
QUESTION:
I know that we now have the ability, with accelerators like the large hadron collider, to accelerate particles very close to light-speed. My question has to do with the mass of these particles at these high speeds; Doesn't the mass approach infinity? And, if so, then wouldn't the gravity be so great as to start to "suck in" everything around it? Seems like it would tear the accelerator apart!
 ANSWER:
ANSWER:
The reason is that a proton has so little mass to start with,
so even if it increases by millions of times it is still very tiny. To see a
representative calculation, see an
earlier answer.
 QUESTION:
QUESTION:
I was just thinking about the structure of atoms being made of protons, neutrons and electrons. Do you know why atoms even have neutrons if the neutrons are electrically neutral? what is the point of having neutrons?
Also, why do they say Pi is squared when it is so obviously round?
 ANSWER:
ANSWER:
The neutron almost does not exist. A free neutron outside a
nucleus is not stable and will decay to a proton, an electron, and a
neutrino in about a half hour. However, it is imperative that there be
neutrons because there is no nucleus, except 1H, which consists
only of protons. A simple way to look at it is that the nuclear force which
protons exert on each other is very strong but, because the protons are so
close to each other inside a nucleus, the Coulomb (electrostatic) repulsion
is also very strong; so you might think of the neutrons as "buffers" which
hold the protons far enough apart that the Coulomb force does not get too
big. During nucleosynthesis in a star, if a nucleus is formed which has one
or two too many protons, it will decay by transforming excess protons into
positrons (anti-electrons), neutrons, and neutrinos.
 QUESTION:
QUESTION:
As far as I know the rotational speed of world is decreasing. Regarding
the Einstein's theories, does that mean the time on the surface of earth
is flowing faster with this decreasing angular speed. Are we having a
time loss bevause of this mechanism?
 ANSWER:
ANSWER:
Someone standing outside watching the earth rotate will find
that your clock runs slower. But, to you, your clock runs at the same rate
no matter how you are moving relative to somebody else; so you will not
notice any difference in the way your clocks run if your motion relative to
somebody else changes, but they will observe a change of your clock rate. If
the earth slows down, the day will get longer but the day is not a reliable
measure of time, obviously, because if the earth stopped altogether time
would not stop.
 QUESTION:
QUESTION:
Why is energy always conserved?
 ANSWER:
ANSWER:
It isn't always conserved. Energy is only conserved in an
isolated system. An isolated system is one on which no outside forces do
work. Work is what changes energy, and if none is done, the energy remains
the same.
 QUESTION:
QUESTION:
I am, for the most part, a biologist, but I always have found physics to be a curious subject and used to study it for a year or two. One of my questions that I hope you can answer involves quantum tunnelling. I am familiar with the basic concept of tunnelling; since quantum objects are "smeared" over an area, they have a small chance of spontaneously crossing a thin enough barrier.
What I am curious about, though, is to what extent this can occur. I have some heard people say that two protons, left to themselves for a long enough time, can spontaneously fuse into a deuteron. I have also heard that, given a long enough time, a car could quantum-tunnel out of its garage, an electron in my fingertip one second could instantly appear at Betelguese the next, or a rock could on incredible timescales behave like a liquid as atoms tunnel out of crystalline strucutres.
What I am curious is - is this actually possible? If my understanding is correct, particles can tunnel but only within a restricted area determined by its mass; an electron can go anywhere in a wide circle, a C60 fullerene may tunnel a distance about its own size, and a comparatively large structure like a virus cannot tunnel since the restricted area is less than its actual size. Could you please explain if it is theoretically possible for anything to teleport anywhere given enough time, or if my understanding is correct tunneling becomes impossible after a certain point?
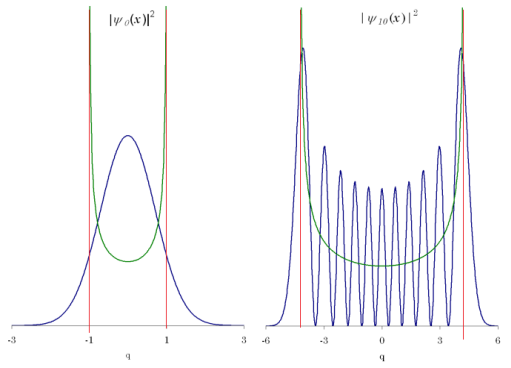
 ANSWER:
ANSWER:
I think this violates the site groundrule stipulating "single,
concise, well-focused questions" but I will touch on a couple of aspects of
tunelling. To the right are shown probability distributions
�the
first for lowest energy, the second a much higher energy�for
a mass on a spring (simple harmonic oscillator, SHO). Classically, when you
set the mass in motion, it oscillates between two points equidistant from
the equilibrium position; those points are shown by the red lines in the
figures. The faster you cause the mass to go (the higher its energy) the
greater the distance between the points (we say the greater the amplitude of
the oscillation) will be. These are called the turning points and if you ask
what the kinetic energy is beyond the turning points, you get a negative
value and since kinetic energy is positive definite all the time, this is
called the forbidden region. The probability distributions for the classical
cases are shown by the green lines and you note that it is most probable to
find the mass near the turning points because it is moving slowest there and
therefore spends most of its time there. The blue lines show the
probabilities for quantum mechanical calculations. If the energy gets very
high, the quantum calculation becomes, on average, much like the classical
calculation. But at low energies it is very different; the lowest energy
state, called the ground state, has the highest probability for the quantum
system in the center which is the lowest probability for the classical case.
But the most interesting thing is that the quantum calculations predict that
there is a probability that the mass will be in the forbidden region and
therefore it will spend part of its time there. You can never actually
observe the particle there but you can prove that it was there by observing
tunneling. Here is my proposed experiment. Looking at the ground state, the
amplitude is
x=�1;
suppose we design a spring so that it behaves normally as long as
x<1.5
but breaks when
x=1.5.
Then classically we will never see the spring break because the mass never
got there. But, quantum mechanics predicts that, if you wait long enough,
the spring will suddenly break and the mass will fly away. This is
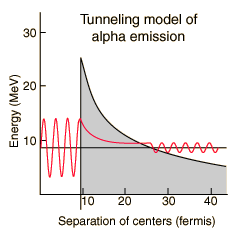
tunneling. Perhaps the most famous example of tunneling is the theory of
alpha-particle decay of heavy elements. The graph to the left shows this
tunneling, showing the energy plotted as a function of the distance of the
alpha particle from the center of a nucleus in which it is bound. The gray
area is called the potential barrier the outline of which is simply the
potential energy of the alpha particle. To make this more intuitive, the
slope of the potential energy represents the force experienced by the
particle whose energy here is a little less than 10. Inside the surface of
the nucleus, the slope is very large from which we can conclude that the
particle is confined to move inside a radius of about 10 fm, and this would
be the classical turning point. However, this is a quantum mechanical
particle and its probability distribution penetrates into the forbidden
zone. But, at larger distances away the force on an alpha particle is very
different; because it and the nucleus are both positively charged, an alpha
particle outside to the right will be repelled which is what is represented
by the gradually decreasing height of the right side of the forbidden
region. Because of the nonzero probabilty in the barrier, it is possible to
leak out and it does�that
is, alpha decay does occur. But even in this microscopic case, lifetimes are
usually very long, millions of years or more.
Your other questions are mostly about
macroscopic things. The car is not like a single particle which might be
thought of as having a wave function and there is no single force on all the
pieces of the car so it becomes about impossible to even think about it.
Even if the car did behave like a single particle, it would be so classical
that any penetration into the forbidden region would be so small that you
would have to wait many universe ages for anything to happen if the car were
in its "in the garage ground state". Two protons are not going to fuse into
a deuteron because charge would not be conserved. An electron in your finger
will not appear somewhere far away; you are maybe confusing tunneling with
entanglement.
 QUESTION:
QUESTION:
My question concerns a bathroom scale that sits on a tile floor. Does my weight on that scale fluctuate at all when the bathroom is very cold? Very cold is the 40's and 50's. I seem to weigh less when it's particularly cold overnight versus a mild overnight temp.
 ANSWER:
ANSWER:
If your scale is mechanical, operates by springs of some
sort, the spring constant (k) will depend on the temperature and the
weight displayed will depend on the spring constant. The constant k
gets larger as the temperature gets lower. Here is the way a spring scale
works: When a weight W is placed on a spring with spring constant k, the spring compresses by an amount
d, and d=W/k;
the scale is calibrated such that a given displacement corresponds to a
given weight. If k gets larger, d gets smaller for a given
weight so the calibrated scale will read a smaller number than the actual
weight. This is probably around a 1% effect, but that would be 2 lb for a
200 lb man. In this scenario, your weight doesn't change, the reading is
incorrect.
 QUESTION:
QUESTION:
Why is the permittivity of free space not 1?
 ANSWER:
ANSWER:
Note that this constant has units, ε0=8.8542x10-12
C2N-1m-2. The permittivity of free space
essentially quantifies the strength of electrostatic forces, F=q1q2/(4πε0r2)
for the force between two point charges. But, if you redefine any of the
units�length, mass, time, charge�you will change the numerical value of ε0.
For example, suppose you define the unit of charge as that charge which when
two 1 unit charges are separated by 1 m they exert a force of 1/(4π)
N on each other; call that unit of charge 1 Baker (B). Then ε0=1.0
B2N-1m-2.
 QUESTION:
QUESTION:
what changes would occur within earth and to its rotation besides the partial loss of gravitational pull due to moon(because sun is also responsible for the gravitational pull of earth) when there is no moon/or when the moon suddenly vanishes?
 ANSWER:
ANSWER:
Certainly the main thing you would notice is that the tides
in the oceans would become very much smaller and with different periodicity.
There are lots of other more subtle effects like the precession of the
earth's axis which would be less noticable in the short term. However, as I
note on the site, I do not answer detailed astronomy questions.
 QUESTION:
QUESTION:
My question deals with quantum entangled particles.
How common are naturally occurring quantum entangled particles?
How would you identify a single particle as being part of an entangled
pair?
 ANSWER:
ANSWER:
I believe the role entanglement plays in nature is pretty
much up to speculation so there is really no information about how common it
is. Some people think that entanglement of many more than two particles is
how we will eventually understand the connections between quantum physics
and classical physics. It seems to me that if you find a particle there is
no way to determine whether it is entangled with another particle (or other
particles) without knowing how it was initially prepared.
 QUESTION:
QUESTION:
I have read that when a pair of particles are entangled their spin is correlated making the particle have opposite spin. Is this also true of the charges of subatomic particles.
 ANSWER:
ANSWER:
No. Electric charge is not a property which lends itself to
entanglement because there is no way to have a mixed wavefunction part
positive and part negative electric charge.

 QUESTION:
QUESTION:
My question pertains to the periodic table of elements. Why is tungsten represented with the letter W? I am assuming that the letter W was the first letter of the person's name who discovered the element- is this correct?
 ANSWER:
ANSWER:
The word tungsten comes from the Swedish, tung sten=heavy
stone. The symbol W comes from the word wolfram which comes from the mineral
wolframite which is the ore which is the principle type of tungsten ore. The
word wolframite comes from the words wolf rahm=wolf soot or wolf
cream because wolframite interfered with the smelting of tin and was said to
"devour" the tin (like a wolf)! Since both tungsten and wolfram come from
the Swedish, you might wonder why it was not given the symbol T. It turns
out that a mineral Sheelite was called tungsten in Sweden and so they chose
to call it wolfram to avoid confusion. Credit for discovery of the element
goes to two Spanish brothers, Jose and Fausto Elhuyar, who isolated it from
an acid made from wolframite in 1783.
 QUESTION:
QUESTION:
Is time dilation possible for objects moving at high speed on the ground. Or, is altitude central to the phenomenon.
 ANSWER:
ANSWER:
The altitude is irrelevant. All that matters is the velocity
of the clock relative to you. (Actually, altitude does matter a little bit
because there is also a gravitational time dilation where clocks in a
gravitational field run at rates which depend on the strength of the field.
But I think you are interested in normal time dilation which depends on
speed. It turns out that both kinds of time dilation must be included in the
software for GPS devices to get the necessary accuracy.)
 QUESTION:
QUESTION:
As far as I understand it, Gravity is measured in units of 'Newtons', however does such information exist with regards to relatable gravitational forces for bodies within our own solar system (i.e. Where Earth would be 1 and Mars 0.5, for example)?
 ANSWER:
ANSWER:
Gravity is a force and may be measured in Newtons (SI system
of units) or pounds (English system of units); 1 Newton=0.225 pounds. I do
not really understand what your question is asking. If you need to find the
force on, say, a 1 kg object at the surface of a planet, you can use the
equation W=MG/R2 where W is the weight (AKA
the force the planet exerts on the 1 kg), M is the mass of the
planet, R is the radius of the planet, and G=6.67x10-11
N∙m2/kg is the universal constant of gravitation. W will
be in Newtons (N) if M is in kilograms (kg) and R is in meters
(m). For example, Wearth=6x1024x6.67x10-11/(6.4x106)2=9.8
N and WMars=6.4x1023x6.67x10-11/(3.4x106)2=3.7
N. So, if you want to quantify earth with 1 unit of gravity, Mars has
3.7/9.8=0.38 units. Be sure to note that the force of gravity depends on
where you are; if you go to a distance r, greater than R, from
the center of the planet, you find that the force of gravity on 1 kg is
given by MG/r2.
 QUESTION:
QUESTION:
This is one of the most baffling physics questions so far. Suppose a cyclist is pedalling briskly, thus accelerating forward. He exerts force on the tyres, the tyres exert force on the ground, and the ground exerts a reaction force which accelerates the cyclist. Right? But now the cyclist applies brakes. Now he starts to retards. But since the tyres are still moving in the same direction, hence friction must also be acting in the same direction. Then which force is responsible for the retardation? I suppose the brakes cannot retard the 'cyclist and the cycle' system, since it is an internal force.
 ANSWER:
ANSWER:
There is nothing "baffling" here. You are right, all internal
forces should be ignored if you want to understand the motion of the
bicycle. The only external forces on the cycle and its rider are its own
weight, the normal force up from the road on the wheels, and the frictional
force between the road and the wheels. (I am neglecting internal friction
and air drag.) The first of these two add to zero (assuming a horizontal
road) and can be ignored for our purpose. If the acceleration is forward,
the friction if forward. If the acceleration is backward, the friction if
backward. The direction of the friction is not determined by the motion of
the wheels because the wheels are not slipping on the road (you hope) so
static friction, not kinetic friction, is responsible for the acceleration.
It is friction which speeds you up or slows you down.
 QUESTION:
QUESTION:
I have a question about particles/waves that travel at the speed of light. When a light bulb emits light, does the light come into being already travelling at the speed of light or does it accelerate up to the speed of light?
Is there a period of time where the light is actually traveling slower than the speed of light?
If there is a period of time where it is accelerating, where does it get the energy from?
 ANSWER:
ANSWER:
In a vacuum, the speed of light is never slower than c=3x108
m/s. It never accelerates. When light travels through a material, say glass,
it travels more slowly but instantaneously changes to c when it
exits. But, its energy does not change when it "speeds up" because energy is
determined by frequency and the frequency does not change when it enters a
material.
 QUESTION:
QUESTION:
Consider a tug of war game. is the net work the ground on the two teams is negative, positive or zero?
 ANSWER:
ANSWER:
Just after one team has won, all players are moving. They
have a kinetic energy. Therefore positive work was done on the whole system
by friction with the ground. Once everyone stops moving, the net work done
on the system would have been zero.
 QUESTION:
QUESTION:
Why is that the heavy things do not bounce much as compared to lighter things though acc. to Newton's law of action and reaction the force exerted on floor by heavier objects is much than that of lighter objects??
 ANSWER:
ANSWER:
First of all, the reason you state for expecting the larger
mass to bounce higher is flawed. Although the larger mass will experience a
larger force when it hits the floor, it is also a larger mass and
therefore harder to accelerate. Newton's second law tells you that the
acceleration depends both on force and mass. The only thing that determines
how high something will bounce is the elastic properties of the floor and
the bouncing object.
 QUESTION:
QUESTION:
I am wondering about some physics in an imaginary underwater habitat:
A 100 m tall moon pool is placed underwater, open at bottom but else closed, and filled with air.
Open entrance is placed on 200 m water depth. What would the air pressure be at the top compared to bottom?
 ANSWER:
ANSWER:
I did not know what a moon pool is. There is a
wikepedia article on
moon pools. There are several kinds, but the questioner asks about one where
the whole tank is submerged with the bottom open. The pressure 200 m below
the surface of the water is determined approximately by a rule of thumb that
each 10 m depth increases the pressure by about 1 atmosphere, so the
pressure at 200 m is about 21 atmospheres. The air pressure in the moon pool
would have to be 21 times atmospheric pressure to keep the water at the
bottom. The pressure at the top would be about the same because there is not
much pressure change over 100 m in a gas.
 QUESTION:
QUESTION:
Why is the probability of splitting an atom greater when sending slow neutrons rather than fast through the nucleus in fission reactors?
 ANSWER:
ANSWER:
If a neutron and a fissile nucleus interact, there is a
probability, not a certainty, that a fission will occur. A slow neutron will
spend much more time interacting with the nucleus and therefore the
likelihood of a fission happening is greater than for a fast neutron which
spends less time interacting.
 QUESTION:
QUESTION:
how can a skydiver control her terminal velocity by changing shape?
 ANSWER:
ANSWER:
The force of air drag can be approximated as
F≈�Av2
where
A
is the area presented to the onrushing air and
v
is the speed of the object. (This is correct only for SI units.) The
terminal velocity occurs when this force is equal to the weight,
mg=�Avterminal2
, so
vterminal=2√(mg/A).
So if she points her body toward the ground like a diver she has small
A
and goes faster or if she spreads her arms and legs out in spread-eagle
fashion she has large
A
and goes slower.
 QUESTION:
QUESTION:
If you where hanging a 35lb piece of pipe with one end in a hanger is the weight your lifting at the other end of the pipe 35lb?
 ANSWER:
ANSWER:
If the pipe is of uniform thickness, you and the hanger would
each hold up half the weight.
 QUESTION:
QUESTION:
How can a fast moving physical ship with a slow ticking clock get to Andromeda 89 thousand times faster than light, as you claim?... 28 years on the ship's slow clock but 2.5 million Earth orbits around the Sun, just for a "reality check."
 ANSWER:
ANSWER:
Where do I claim that? I do not know what you are talking about.
 REPLY:
REPLY:
So sorry! I mistook your site for Dave Goldberg's site,
Ask *a* Physicist, where I read his claim awhile back on his
"We Can Make It to the Edge of the Observable Universe in a Few Decades" article/blog. I take it that you do not agree with him.
 ANSWER:
ANSWER:
OK, I found Goldberg's site and everything he says is
perfectly correct. In fact, I found a
similar answer on my site
which we can use for comparison. The speed which Goldberg uses is 99.9999999999999999998% of
c. In my calculation I used a very fast speed
but much slower than his, 99.999% of c. When I calculated the
elapsed time on the ship I got about 11,000 years, he got only 28 years. My
ship was going the same speed the whole time but his started from rest and was constantly
accelerating, so he would have gotten a smaller time yet if his ship had
been going with a constant speed the whole time; if the Goldberg space ship
had been going 0.999999999999999999998c
the whole way, it would get to Andromeda in about an hour, its time! Your
problem, I think, is how either his or mine could be right since it takes
2.5 million years for light to travel that distance, right? But, it depends
on who is measuring the time. An observer on earth will see the light take
2.5 million years to get there and the space ships arrive just a
little (compared to 2.5 million years) later. But an observer on the space ships will see a greatly
shortened distance to Andromeda, so he will observe both himself and light
to take a much shorter time to get there, the light always just beating
the space ship. You are right, nothing can travel faster than light, but
everybody sees the same light speed in their own frame; there is no
contradiction in saying one observer sees light taking 2.5 million years to
travel between two points in space while another observer sees light as
taking 10 years to travel between the same two points.
 QUESTION:
QUESTION:
Why transverse waves cannot travel in air and interior of liquids even though they can travel in solids where particles are strongly packed together?
 ANSWER:
ANSWER:
A wave requires that there be restoring forces between atoms
of the medium. For longitudinal waves to happen, there must be such
restoring forces with atoms along the direction the wave is traveling; this
can happen with solids, liquids, or gases and essentially the waves are
pressure waves. For transverse waves, there must be restoring forces
perpendicular to the direction of the wave velocity (often called "shear
forces") and liquids and gases cannot support such shear.
 QUESTION:
QUESTION:
Trying to understand physics concepts is
an interest of mine. I was hoping you could shed some light to help my
understanding? The equation for Kinetic Energy: KE = 1/2 m v2.
I understand the value of velocity squared in that; the kinetic energy
of an object is proportional to its speed squared:double the speed,
quadruple the KE. But I am having trouble with why and what the 1/2
value is telling me about what is going on in the equation as to the
motion of mass and speed. It is pretty elementary stuff but if I want to
know about Energy, Work, Power and Heat I need to get the basics right.
 ANSWER:
ANSWER:
To do this on the simplest level, you need to know kinematics
for uniform acceleration [x=x0+v0t+½at2
and v=v0+at where the 0 subscripts denote the
position and velocity when t=0] and Newton's second law [F=ma].
Suppose that you have a constant force F that you exert on a mass m over a distance
s; the work done is W=Fs and work
changes the energy; that is, we say that the work done equals the energy
given to m. I will assume that m begins at rest and at the
origin, so x=s=½at2 and a=v/t; then
F=mv/t and s=½(v/t)t2=½vt.
Finally, W=Fs=(mv/t)(½vt)=½mv2.
So, in the case of a constant force, the factor of ½ comes from the
½at2
part of the kinematic equation for position.
 EXTRA ANSWER:
EXTRA ANSWER:
If you know calculus, this is much simpler. Write dW=Fdx
and F=m(dv/dt) so W=0∫sFdx=0∫sm(dv/dt)dx=0∫vm(dx/dt)d
v=0∫vmvdv=½mv2;
and this does not require F to be constant.
 QUESTION:
QUESTION:
why do we need to have a new expression for calculating the kinetic energy of a body that is in rotational as well as translational motion?
 ANSWER:
ANSWER:
Whether you do or not depends partly on how the object is
moving. For example, if the object is rolling on a surface without slipping,
it is instantaneously rotating about the point (or line) of contact and you
can write K=½Iω2 where I is the moment of
inertia about that axis; however, you could also show (using the parallel
axis theorem) that K=½Mvcm2+½Icmωcm2
where vcm is the speed of the center of mass, ωcm
is the angular velocity about the center of mass (which is the same as
ω) and Icm is the moment of inertia
through the center of mass. For an object not rolling, K=½Mvcm2+½Icmωcm2
is still the correct expression for kinetic energy at any instant but
you can no longer write the kinetic energy as pure rotation as you could for
the rolling object because there is no relationship between vcm
and ωcm.
 QUESTION:
QUESTION:
In the TV-series Stargate SG-1 a Goa'Uld Ha'Tak is capable of going 50% lightspeed with sublight engines. Wouldn't these kinds of speeds already be relativistic and what happens excactly to the crew in the ship when the relativistic effects start? And what is the minimum relativistic speed in which relativistic effects become noticeable? A friend of mine said that at 8% lightspeed relativity kicks in making space travel above 8% lightspeed really challenging.
 ANSWER:
ANSWER:
Where you need to start doing calculations relativistically
depends on how accurate you want to be. The factor which determines the
magnitude of relativistic effects is usually γ=√(1-β2)
where β is the ratio of the speed to the speed of light. For example
if β=0.1, 10% the speed of light, then γ=0.995 which would
mean only about 0.5% error using nonrelativistic calculations. For β=0.5,
50% the speed of light, γ=0.
867,
still only about 13% error. But, there are no "relativistic effects" for
somebody on the ship; everything appears normal on the ship. They would,
however, see distances to objects toward which they are traveling shrink. I
do not know what it means that "space travel…[is] really challenging". Of
course, it is challenging to get to relativistic speeds in the first place,
but I do not see any hazards "kicking in" at
β=0.08.

 QUESTION:
QUESTION:
Hi! I was playing a video game called "Mass Effect 2" and in the game a drill instructor gives a lesson about the main gun of a Mount Everest class dreadnought that is the first dreadnought class made by largest human government in ME universe known as Systems Alliance. The main gun is a rail gun that accelerates one 20kg ferrous slug to 4025 km/s and it takes 5 seconds to charge. The slug impacts with kinetic energy of 162006250000000 joules which is 38,7 kt of tnt. The main gun is 800 meters long and built into the superstructure of 888 meter long dreadnought that has mass of at least one milloin tons. Would there be any problems of having our future warships operating in space equipped with this kind of weapon and does this design sound feasible? And in the game's lore it is stated that an impact from this weapon levels entire cityblocks. Would this projectile moving at 4025km\s be able to level a cityblock in a metropolitan area because the Turians (a species in Mass Effect) fired these slugs to human cities on the colony of Shanxi leveling a cityblock clean of even the sturdiest skyscrapers.
 ANSWER:
ANSWER:
Gamers and sci-fiers have asked questions like this before.
That is good, to think about the physics and how it might affect the
practicability of these kinds of weapons in the real world. You might also
be interested in a couple of earlier answers regarding the game
Halo and the movie Eraser.
Your numbers are right, the kinetic energy of a 20 kg mass traveling at a speed
around 4x106 m/s is about 1.6x1014 J.
(The speed is just a little above 1% the speed of light, so classical
calculations should be ok.) As I noted in the Eraser answer, the energy of
the atomic bomb dropped on Nagasaki was about 1014 J, so this
should answer your question about whether or not there is adequate energy to
demolish a city block�easily!
-
It takes 5 s to
charge, so let's see what the required power input would be: P=E/t=1.6x1014/5≈3x1013
W=30 TW. The average power consumption of the entire earth is 15 TW.
Where are you going to get this kind of power in the middle of empty
space? Maybe you can just carry hundreds of atomic bombs with you?
-
And, let's talk
about the launch. If the acceleration over the 800 m is uniform, it
would take about 4x10-4 s resulting in an acceleration of 1010
m/s2. That means that the force necessary to give this
acceleration to a 20 kg mass is 2x1011 N≈45 billion pounds.
Do you think an iron slug could withstand such a force?
Given the time of acceleration, what is the
power delivered to the slug? P=E/t=1.6x1014/4x10-4
s≈4x1017 W.
Unlike the previous two answers, recoil for this
gun should not be a serious problem. If the mass of the ship is a
million metric tons, 109 kg, the recoil velocity should only
be about 20x4x106/109=8 cm/s.
I think you would agree that this device would be
totally unworkable in the real world.
 ADDED
COMMENT:
ADDED
COMMENT:
In my comment above stating that recoil would not be a
problem, I have to take that back. Even though 8 cm/s is not very fast, that
speed is acquired in a very short time, 4x10-4 s, so the
acceleration of the ship is very large, a=0.08/4x10-4=200
m/s2 which is approximately 20g, quite a jolt!
 QUESTION:
QUESTION:
When two objects with mass are placed together, do they actually ever touch or is there a space between the objects on a microscopic level?
 ANSWER:
ANSWER:
It gets tricky to define what you mean by "touch". When you
get to a microscopic level, there is no way to actually define what the
surface is, it is fuzzy rather than sharp. The surface is comprised of the
outer electrons of the atoms and these are charged; hence they repel each
other and since the electric repulsion gets greater as the electrons get
closer, you might think of the upper object "floating" above the lower. It
is actually something called the "electron
degeneracy pressure", the Pauli exclusion principle which prevents
electrons from occupying the same quantum state, which keep the electrons
apart.
 QUESTION:
QUESTION:
I can not replicate a photoelectric experiment where I place a cylinder made out of zinc that leads to #10 copper wire to 2 aluminum foil leaves.
I shine a flashlight on the zinc cylinder and the aluminum leaves will not split. How can I properly make this experiment work?
Please note that I can bring an object charged with static electricity close to the zinc cylinder and it does make the aluminum leaves spread.
I am however trying to use light instead. Do I need a different kind of light?
 ANSWER:
ANSWER:
The photons in visible light do not have enough energy. Try
ultraviolet light.
 QUESTION:
QUESTION:
How many particles do the particle accelerators at most accelerate when they are running experiments? One, ten, hundreds or thousands?
 ANSWER:
ANSWER:
When I was doing experiments some years ago, typical beam
currents were on the order of a few nanoamperes. Usually, these were protons
which each have a charge of 1.6x10-19 C. So, suppose the beam
current is 16 nA=16x10-9 C/s; then the number current is [16x10-9
C/s]/[1.6x10-19 C/proton]=1011 protons/second, about
100 billion. At the LHC in Europe, the intensity is much larger, on the
order of 4x1018 protons/s which would correspond to an average
current of about 0.6 A. The high number intensities are vital because the
events physicists are looking for are extremely improbable. The LHC is a
pulsed machine, its beam is a series of very short pulses. So, the
instantaneous current during a pulse is much larger than the average
current.
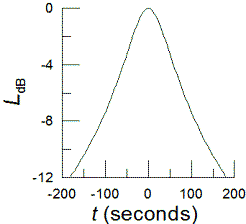
 QUESTION:
QUESTION:
Given a airplane at speed 600 knots, whose track at its closest point passes by one at 15 kilometers away (elevation angle not important,) what are the formulas that would describe the shape of the decibel readings over time? (which are something like 25 25 40 40 40 38 36 34 30
25 25, with 25 dbA being the background.)
 ANSWER:
ANSWER:
I will call the distance of closest approach (15 km) d,
the speed (600 knot=0.309 km/s) v, the distance between the plane and
observer r, and choose t=0 to be the time of closest approach.
Assuming that the sound from the plane is isotropic (a relatively poor
assumption), the intensity of the sound is proportional to 1/r2=1/(d2+v2t2),
so I(t)=C/(d2+v2t2);
note that this is not dB but something like watts/m2. I is
an absolute intensity (power/unit area), dB levels measure relative levels
on a logarithmic scale. I will call
the maximum intensity I0=C/d2 and
the dB level relative to the maximum is given by LdB=10∙log10(I/I0)=10∙log10(d2/(d2+v2t2)).
The graph to the right shows the plot for your numbers.
 QUESTION:
QUESTION:
Underpinning so many theories in physics is time.
Within physics itself is there a theory about time?
It seems to me that time is just something that is a fabrication that can be expressed on either side of an equation, despite that time has an "arrow"
that only goes in one direction. There is no solid evidence to the contrary.
Is this a physics problem or a philosophical one?
 ANSWER:
ANSWER:
I have heard or read many eminent theoretical physicists who
state something like "we would understand nature much better if we
understood what time is". There is a recent book by Lee Smolin,
Time Reborn: From the Crisis in Physics to the Future of the Universe,
which addresses the nature of time. It is written for a lay audience but if
you are not a physicist you might find parts of it tough going.
 QUESTION:
QUESTION:
is work energy theorem valid in non inertial frames?
 ANSWER:
ANSWER:
The work-energy theorem says that the change in kinetic
energy of an object is equal to the work all forces do on it. Imagine that
you are in an accelerating rocket ship in empty space, a noninertial frame.
You have a ball in your hand and you let go of it. You observe this ball to
accelerate opposite the direction in which the ship is accelerating and therefore see its kinetic energy change. But, there are no
forces acting on it so no work is done. Another way you could come to this
conclusion is that the work-energy theorem is a result of Newton's laws and
Newton's laws are not valid in noninertial frames. You can, though, force
the work-energy theorem to be valid if you introduce fictitious forces, a
way to force Newton's laws to work in noninertial frames. (Centrifugal force
is an example of a fictitious force.) If you invent a
force on the objects of mass m in the accelerating (a)
rocket ship above of Ffictitious=-ma,
this force will appear to do the work equal to the change in kinetic energy.
 QUESTION:
QUESTION:
if a laser beam is a stream of photons concentrated in a narrow direction, how come we can see it from aside?
 ANSWER:
ANSWER:
You can only see it if some of the photons scatter off
something in their path—dust or smoke in the air, for example.
 QUESTION:
QUESTION:
What would happen if an extremely red hot nickle ball was placed in a vacuum?
 ANSWER:
ANSWER:
It would cool by radiation. When it reached the point where it was absorbing the same amount of radiation
energy from its surroundings as it was radiating itself, it would remain at that constant temperature.
 QUESTION:
QUESTION:
First, how much energy (in the most basic sense) does a car expend driving at a moderate speed for one mile. Next, how big would a spring have to be (roughly) to store the energy equivalent of what that car expended during that mile.
 ANSWER:
ANSWER:
I can only do a rough estimate. Suppose your car has an
internal combustion engine and gets 40 mpg. The energy content of 1
gallon of gasoline is about 120 MJ, so you would use about 120/40=3 MJ
of energy per mile. But, a typical engine has only about 20% efficiency,
so the energy supplied to the car is only about 0.2x3=0.6 MJ=600,000 J.
Now, you want to store that much energy in a spring. For a spring, the
energy stored is ½kx2
where x is the amount by which it is compressed (or stretched) and k is the spring constant which is determined by how stiff the spring is.
(The constant k can be measured by k=F/x where F
is the force you have to exert to stretch or compress it by x.)
Clearly, the bigger k is the less the spring will have to be
compressed to store a given amount of energy. The coil spring of a car, a
pretty stiff spring, has a typical spring constant of k≈25,000 N/m,
so to store 600,000 J of energy, 600,000≈½∙25,000x2
or x≈7 m! I do not see much possibility of having a spring powered car. You
probably had in mind a spiral spring like a watch spring, but to store that
much energy in any kind of spring is going to be impractical.
 FOLLOWUP QUESTIONS:
FOLLOWUP QUESTIONS:
Thanks for helping me with that.
I will admit that I'm still a little unclear about the answer though.
You are correct that I am wondering about a spring powered car but I definitely would not use a spiral spring. A compression spring would probably work best.
I don't understand your final answer. I am getting lost in the spring conversion formula. What does the final answer mean in layman's terms please?
 ANSWER:
ANSWER:
The spring would have to be compressed by 7 meters. That would mean that it would need to be at least twice that long, about 40 feet! You could use a stiffer spring
(see below) to get a smaller required compression, but imagine the force you would have to exert to compress it. Keep in mind that you would have to supply the energy to the spring in the first place, a lot of energy.
I know this spring is not going to work, but how much force would it
take to hold it compressed by 7 m? F=kx=25,000x7=175,000 N≈40,000
lb. Another issue is that as the spring unstretches, the force it exerts
gets smaller, so you would need to have some kind of governor mechanism
to deliver the energy smoothly.
 CONTINUED
CONTINUED
Also, there are two things that are working in favor of the feasibility of the spring car:
I know from researching that there are many other factors that affect the gas- to engine- to -transmission to -wheels to- road, etc cycle so that the total efficiency of the entire loop would be far less than 20%.
 ANSWER:
ANSWER:
This is taken care of by the fact that I have specified the
miles per gallon for the hypothetical car. The miles per gallon you get is
determined by how well you have minimized the effects other than engine
efficiency, mainly frictional effects. You asked for an estimate of the
energy which the car would use to keep going a constant speed, and this is
the best way I can think of doing that. Here is another way to estimate the
energy consumed: suppose that I push on the car to keep it going a constant
speed. I could probably do that with a force of about 100 lb≈445 N; one mile
is about 1600 m, so the work I do is the product of the force times the
distance and the work I do is the energy I use: W=445x1600≈712,000 J.
(Actually, I am pretty impressed by how close this is to my other estimate
of 600,000 J! It's just an accident that they are so close, but good that
they are of the same order of magnitude�it increases my confidence that the
energy consumed is pretty well approximated.)
 CONTINUED
CONTINUED
Despite my very basic and incomplete understanding of the formulas that give exact measurements for potential energy in springs and the potential energy available in compressed air it is obvious to me that if a car can run 300 miles off of a bottle of compressed air and a compressed air driven motor (these cars already exist and are in production in places like holland, india, etc) then a large spring perhaps three feet long and two feet around with a wire diameter of over half an inch could at least do the same.
Getting the potential energy out of the spring in a useful way to power the car is another ball of wax altogether though.
 ANSWER:
ANSWER:
If you want a 3 ft long spring, about 1 m, the most you
could probably compress it is about a half meter. To store 600,000 J of
energy, the equation would be 600,000=½kx2=½k(0.5)2=k/8,
and so the spring constant would be k=4,800,000 N/m. Then the force
to hold it at 0.5 m would be F=kx=2,400,000 N≈540,000
lb. If you were not faced with such enormous forces, like if you just wanted
to have a toy car go a few meters, you could certainly get the energy out of
the spring with a cleverly designed gear box; but the structural problems
you would face with forces of hundreds of thousands of pounds would be
insurmountable, I believe.
 QUESTION:
QUESTION:
How can time exist in space if time is a man made tool we created to monitor the revolution of our earth around our own star? Once you left this solar system time would have no concept. you wouldn't be able to monitor it would you?
How can Einsteins theory of relativity be real if time doesn't exist in space. He says that (earth time) passes slower for an object travelling at the speed of light through space, but how can you monitor that on a clock (still on earth time) in space where time doesn't exist?
Our sun is not the centre of our galaxy, it's not even the centre of our universe so the way we control time would not make a difference at any other point in space, An object travelling at the speed of light would still be in the same moment as us but there watch wouldn't be correct as the time it showed would be useless to there point in space.
 ANSWER:
ANSWER:
You are totally off base here. Measurement of time has
nothing whatever to do with the motion of the earth. You may think of it
that way and ancient man certainly thought of it that way, but today the
second is defined in terms of an atomic clock which would tick at the same
rate anywhere in the universe. The official definition of the second is: "The second is the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom."
If I have an atomic clock and you have an identical atomic clock which you
take on a high-speed trip away from and back to me, when you return we will
find that your clock ticked fewer times than mine. (See the
twin paradox.)
 QUESTION:
QUESTION:
This video
states, at the end, that photons do not experience time or distance. Proof?
 ANSWER:
ANSWER:
This kind of statement always kinda drives me nuts. A photon
does not have a point of view, cannot "experience" anything; it is an
inanimate thing. But it has even less of a point of view than a proton or
any other particle with mass because it is physically impossible to carry a
clock or a meter stick along with it, so how could it possibly experience
time or space?
 QUESTION:
QUESTION:
can u explain me use of earths mass in kepler's third law
 ANSWER:
ANSWER:
The force F between the earth and the sun is F=K/r2
where r is the separation, K=GMsunMearth,
G is Newton's universal constant of gravitation, and the M are
the masses. Kepler's third law states that T2=4πμa3/K
where T is the period of the orbit, a=K/(2E)
is the semimajor axis of the orbit, and
μ=MearthMsun/(
Mearth+Msun)
is the reduced mass of the two-body system. So, the earth's mass enters
through
μ,
a, and K. It turns out that if
Mearth<<Msun,
the period is approximately independent of the mass of the earth. You might
be interested in
earlier
answers which explore Kepler's laws in more detail.
 QUESTION:
QUESTION:
Is there something wrong with the theory that says, if there is enough dead matter from dying stars that comes together, gravity will take over and eventually produce a new star from this dead matter?
I am aware that stars form from hydrogen, but what if 999 trillion tons of the heaviest known elements got together all in one place? Most say a star would not form because there is no hydrogen, but what then? It would appear that gravity, being indiscriminate, will continue crunching this big iron ball until critical mass is surpassed, regardless of what the result might end up being. What would that result be?
 ANSWER:
ANSWER:
As I state on the site, I usually do not do
astronomy/astrophysics/cosmology questions, so take my answer here with a
grain of salt. But, sometimes the question is sufficiently interesting to me
that I attempt an answer. I would say that a "normal star" might be defined
as an object which makes energy by
nuclear fusion, fusing light nuclei to heavier nuclei. However, when you
reach iron on the periodic table you no longer gain energy by fusing nuclei
and therefore the energy production ceases. Before the whole star becomes
iron, though, other instabilities cause the star to, in one way or another,
end its life, the details depending on the mass of the particular star. The
most dramatic end is a supernova (of which there are several types, again
depending on details), a very dramatic explosion of the whole star; the
energy from such an event is what is generally thought to be responsible for
creation of heavier elements beyond iron. One possible end following a
supernova explosion is called a neutron star. The remnants of the star,
mostly heavy elements like you refer to, will undergo gravitational collapse
and, in essence, electrons will be pushed into protons such that the star is
made mostly of neutrons and is extraordinarily dense (it is essentially a
giant nucleus). With sufficient mass, that is what I believe would happen to
your collection of heavy elements. However, your number, about 1018
kg, is way too small for the requisite mass. Neutron stars have about
1.4-3.2 solar masses and the mass of the sun is about 2x1030 kg.
 QUESTION:
QUESTION:
In the case of a block that's dropped some vertical distance onto a spring,
it's reasonably easy to compute this value & to find the KE of the mass just before it hits the spring, hence the velocity.
What doesn't ever seem to be explained is what happens to the block's acceleration ("g" when it hits the spring). The motion of the block continues downward, but now the net force is Fnet = kx - Weight = ma, not Fnet = mg. This means that the acceleration continues to be positive as the block compresses the spring, but @ a slower rate. This also means that the velocity continues to increase until all the block's PE is converted to spring elastic energy (Eelastic). At maximum compression the block stops
& motion ceases. Since the ideal spring is massless there are no losses due to friction, heat, sound, et. al.
Where does the Vmax occur? It's hard imagine for Vmax to happen @ the instant it stops? Is this process for the spring's resisting force linear?
 ANSWER:
ANSWER:
OK, suppose the speed when it hits the spring is v0.
Choosing +y to be up and y=0 at the end of the uncompressed
spring, may=-mg+k(-y). (Note that when the
spring is compressed its force is upward and y<0 so the force is in
the +y direction; this is why I write the force of the spring as k(-y).
Now, until y=-mg/k, the acceleration is negative (points down)
and the mass is still speeding up; below that point, the net force is
positive (points up) so the mass slows down. Therefore the greatest velocity
will be at y=-mg/k. Note that this position would be the
equilibrium position if you gently placed m on the spring. You could
also get this answer with energy conservation; using the same coordinate
system, E=½mv02=½mv2+½ky2+mgy.
This can be rearranged to give v2=-(k/m)y2-2gy+v02;
if you differentiate this with respect to y and set equal to zero,
you find y=-mg/k for the maximum velocity position. At that
position you can solve for the speed, v=√[(mg2/k)+v02].
The key here is that you need to be very careful
with the coordinate system and the signs of forces and potential
energies. If you do not choose +y up, the potential energy will
not be mgy (it would be -mgy). If you do not choose the
unstretched spring as zero potential energy for the spring, ½ky2
will not be the potential energy.
 QUESTION:
QUESTION:
I have a question, when you drop a solid sphere of aluminum into a bucket of water sitting on the ground. The buoyant force equals the weight of the water displaced, which is less than the weight of the sphere, so it sinks to the bottom. If you take the bucket with you on an elevator that accelerates upward, the apparent weight of the water increases and the buoyant force on the sphere increases, too. Could the acceleration of the elevator be great enough to make the sphere pop up out of the bucket of water?
 ANSWER:
ANSWER:
The easiest way to understand this problem is to use the
equivalence principle which says, briefly, that there is no way you can
distinguish between being in a uniformly accelerated frame and being in a
uniform gravitational field. Your case is a little more complicated since
you are in an accelerated frame which is in a gravitational field. But the
equivalence principle says that if you elevator has an acceleration a,
all experiments you might do would have the same results as if you were not
accelerating but in a field whose acceleration was g+a. But, if you
were in a gravitational field with acceleration g+a, the weight of
the displaced water would be Mw(g+a) and the weight
of the aluminum would be Ma(g+a) where Ma
and Mw are the masses of the aluminum and displaced water,
respectively. In other words, the weight and buoyant force increase
proportionately so that the buoyant force would always be smaller than the
weight.
 QUESTION:
QUESTION:
A newsday article "For safety's sake" was about the backseat bullet. They said that in a 35 mph front-end crash, a 30 pounds child in the back is hurled forward with equivalent force of more than 2000 pounds. Can you please tell me the steps to get to that answer.
 ANSWER:
ANSWER:
A statement like this is total nonsense. Anybody who knows
anything about physics knows that you cannot associate a force with a speed.
To understand why, see my FAQ page, here
and here.
 QUESTION:
QUESTION:
If I wear earmuffs that lower the noise by 20 decibels and then put on earplugs that lower the noise by another 20 decibels will this all combine to 40db noise reduction?
 ANSWER:
ANSWER:
The relative decibel level L is determined by the ratio of
the power levels of two different levels: L=10∙log10(P1/P0).
This can be written as P1=10L/10P0.
In your case, I will say that P1>P2>P3
and the relative dB levels are 20 dB for P1
and P2 and 20 dB for
P2 and P3. So, P1
=1020/2P2=100P2
and P2=1020/2P3=100P3.
If you combine these you find that P1=10,000P3=1040/10P3.
So, the answer to your question is yes, 40 dB is the relative decibel level
for P3 and P1.
 QUESTION:
QUESTION:
If two bulbs one of 60 watt and other of 100 watt are connected in series then 100 watt will glow more but I don't Know why?
 ANSWER:
ANSWER:
If the power rating of a bulb is P, this means that
P watts are consumed if a voltage of 120 volts is across it, so
P=IV=I2R=V2/R=1202/R,
so R=1.44x104/P. So, the resistance of each bulb is
R100=144 Ω and R60=240 Ω. When in
series, the same current passes through each and so the power is P=I2R.
It looks to me like the 60 watt bulb will be brighter because its resistance
is larger. For example, if the voltage were still 120 V, the current would
be I=120/(144+240)=0.313 A. The powers would then be P100=(0.313)2x144=14.1
W for the 100 watt bulb and P60=(0.313)2x240=23.4
W for the 60 watt bulb.
 QUESTION:
QUESTION:
In many popular books and videos that attempt to explain Special and General Relativity I noticed that they all mentioned(so far) that there was no test to determine whether a person inside a box moving at a uniform acceleration could distinguish between the force they experience as either gravity or uniform acceleration.
You probably know where I'm going with this.
But one can test the difference from inside the box.
If the box is sitting on the Earth there would be a "gravity gradient"
in the box. What you weigh at the floor of the box would be different than if you weighed yourself close to ceiling.
In an accelerating box absent any gravitational forces you would weigh the same anywhere inside the box.
Is this a valid observation?
I wonder why the lecturer or writer
leaves this out?
Is there something I'm missing?
 ANSWER:
ANSWER:
It is generally understood that the equivalence principle
states that uniform acceleration is indistinguishable from a uniform
gravitational field. Admittedly, many authors neglect to say this explicitly
since mostly we think of the gravitational field on earth as uniform even
though, as you point out, that is only an excellent approximation for
relatively short distances.
 QUESTION:
QUESTION:
the speed of light in a vacuum is 300, 000, 000 meters per second or just a little less, but what was the recording of this speed relative too ?
 ANSWER:
ANSWER:
That is the fascinating thing about light—its speed is
independent of who measures it. It is a universal constant. This seems
counterintuitive, but has been verified by many experiments. To learn more
about the constancy of the speed of light, see my
FAQ page.
 QUESTION:
QUESTION:
Need to scale a physical object up in size, either double or quadruple. It's a circular acrylic plate, with multiple weights attached around it's edge, to lower the resonant frequency to a specific frequency, 32hz.
The plate is 16" in diameter, the weights around it's edge add up to 1.05 kg. It needs to be scaled to 32" or 64". It will scale in diameter but not thickness, which will remain 1/8" for all diameters.
If the size is doubled to 32", along with doubling the weights around the edge to 2.1 kg, will the resonant frequency be lowered to the same frequency as the 16" plate with 1.05 kg weights?
If not, how does this scale? How far off approximately will the resonant frequency be from 32hz?
Same question for scaling to 64" with 4.2 kg weights around the edge.
 ANSWER:
ANSWER:
Doing a precise calculation like this is impossible without
more details about where the weights are placed. Even then it is extremely
complicated and beyond the scope of my site to do; a circular disc
calculation always involves Bessel functions, neither simple nor intuitive.
However, I know that your scaling will not work the way you expect; I will
show you how I reached that conclusion. To make sure you understand
oscillating systems, let's start by considering a coil spring attached to a
mass m; the stiffness of the spring is characterized by a quantity
called the spring constant k; if it takes a force of F to
stretch the spring a distance D, then k=F/D. The
frequency of oscillation of this mass on this spring turns out to be f=(1/2π)√(k/m).
So, you see, the mass on a spring behaves the way you want—if you double
both the spring constant and the mass, the frequency is unchanged. Now, you
can think of your disc like a spring: if you hang weights around the
circumference it will warp down from the center. The more weight you hang,
the more it will warp, just like a coil spring stretches in proportion to
the force. As an approximation, since I cannot do a disc, I figured a leaf
spring would be the next best thing. So, I found a
calculator
on the web which calculates the stiffness (spring constant) of a leaf
spring. I found that if you double the length of any given leaf spring, you
decrease the spring constant by a factor of 8. So, if you had a leaf spring,
doubled its length, and doubled its mass, the frequency f' would be
f'=f√[(k'/m')/(k/m)]=f√[((k/8)/(2m))/(k/m))]=32/4=8
Hz. For a leaf spring you have to decrease the mass 8 times to keep
the frequency constant. Your disc is not a leaf spring, but it is more
similar to that than to a coil spring. Now, if you think about it, it should
be intuitive that you have to decrease the mass: a bigger disc will be
easier to bend (smaller k) and putting more load (bigger m) on
it will make the frequency (which depends on the ratio k/m)
far from the original frequency. I haven't told you how scaling works for
your specific system, but I hope I have pointed you in the right direction.
If the weights can be fairly easily varied, trial and error (known as
"tuning" here) might be your best bet.
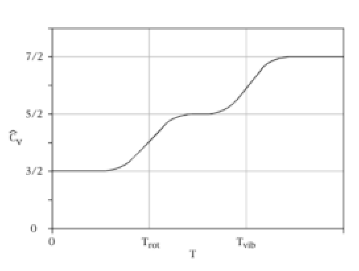
 QUESTION:
QUESTION:
my teacher had me specifically look up the answer to this question but really not understand any other answer what these other sites are giving me. any help? " in addition to the molecular to-and-fro vibration assoicated with temperature, some molecules can absorb large amounts of energy in the form of internal vibrations and rotations in the atoms making up the molecules. would you expect materials composed of such molecules to have a high or a low specific heat?"
 ANSWER:
ANSWER:
I want to keep it fairly simple, so let us consider only monatomic (single
atoms like He or Ar) and diatonic molecules (two atoms, like O2
or H2). I will also talk only about CV,
specific heat at constant volume. The specific heat at constant pressure, CP, is simply related to it by
CP=CV+R
where R is the universal gas constant. Also, this discussion is only
applicable to ideal gases and many real gases are well approximated as
ideal gases, at least for understanding specific heat qualitatively.
Specific heat is the amount of temperature increase resulting from a
certain amount of energy added to the gas. Temperature is a measure of
the energy content of the gas, so adding energy to a monatomic gas
increases the average kinetic energy per molecule ½mv2=½m(vx2+vy2+vz2).
It is said that a point mass has three degrees of freedom (called
translational), x, y, and z, three ways to accept the
energy as it turns out. There is a famous theorem called equipartition of
energy which says that each degree of freedom accepts 1/f of the
energy added where f is the number of degrees of freedom for the
molecule. Then, it may be shown that CV=3(½R);
in other words each degree of freedom contributes ½R to CV.
This can be generalized to higher degrees of freedom so that CV=f(½R).
Now let us think about a diatomic molecule, visualize a dumbbell. A rotating
dumbbell has energy, so a diatomic molecule has another way to accept
energy. It can also vibrate, so there is another way it can accept energy.
These are additional degrees of freedom, so the specific heat must increase.
However, there is an important proviso due to quantum mechanics—to excite a
rotational or vibrational state in a molecule requires some minimum energy
and so, at very low temperatures, only translational degrees of freedom will
be available. But as the temperature increases, first rotational and then at
higher temperatures vibrational degrees of freedom can start taking the
added energy. Hence the specific heat is dependent of temperature as shown
to the right for a diatomic gas (note that ĈV=CV/R).
Let's see if we can understand this (refer to the figure at the left above).
The dumbbell can not rotate about its own axis, only about an axis
perpendicular to the line connecting the two atoms, but there are two such
axes as shown by the red diagram; so, there are two degrees of freedom
because of rotation. As shown by the graph of the specific heat, it starts
out at 3R/2 but when the temperature gets high enough the two
rotational degrees of freedom begin to contribute giving 5R/2 as
expected. As the temperature gets higher yet we see two more degrees of
freedom apparently contributing because the specific heat increases to 7R/2;
this is due to the molecule now being able to vibrate. But, this is a puzzle
because there is only one degree of vibrational freedom, the molecule can
only vibrate along its own axis. The reason is kind of technical: the
vibrational energy has both potential and kinetic parts and each behaves
like a degree of freedom. If you think this is complicated, imagine how it
goes with more complex molecules!

 QUESTION:
QUESTION:
the question is "why does dust fly off when a hanging carpet is beaten with a stick?" Now some people answer it is due to inertia some say it is due to inertia and newton's third law. I think it is due to inertia and Newton's third law because when we hit the carpet the dust particles also jump in the in the direction in which we hit it. If it is inertia only then it must jump in opposite direction. So please clear the confusion.
 ANSWER:
ANSWER:
The reason that the dust is on the rug in the first place is
that there is an adhesive force between the dust and the fibers of the
fabric. When you strike the rug with the stick, many of the fibers are
caused to have an acceleration. If a fiber accelerates, the dust attached to
it must accelerate and that acceleration can only be provided by the force
adhering it to the fiber; but that force is not big enough and so the dust
separates and is then subject to air currents which carry it away. In that
sense, I guess that inertia would be the explanation, but I fail to see why
this means it "must jump in the opposite direction". Further, I do not see
what Newton's third law has to do with anything here. The only force on the
dust is the force due to the fiber and the dust exerts an equal and opposite
force on the fiber; but the fiber, being so relatively massive, is almost
totally unaffected by the force from the dust.
 QUESTION:
QUESTION:
Hello, this is a pretty straightforward question but for some reason I
can't find out this answer online. Apparently, the speed of electricity
in a vacuum is the same as the speed of light. This "source" also says
electricity goes almost at the speed of light but how fast "exactly"
does electricity move through air? Preferably I'd like the answer in
meters/second but I can convert the units myself.
http://en.wikipedia.org/wiki/Speed_of_electricity
right at the top of the second part, it says: "The speed at which energy
or signals travel down a cable is actually the speed of the
electromagnetic wave, not the movement of electrons. Electromagnetic
wave propagation is fast and depends on the dielectric constant of the
material. In a vacuum the wave travels at the speed of light and almost
that fast in air. Propagation speed is affected by insulation, so that
in an unshielded copper conductor ranges 95 to 97% that of the speed of
light, while in a typical coaxial cable it is about 66% of the speed of
light." I need to know I'm hoping that it moves at more than half the
speed of light
 ANSWER:
ANSWER:
The problem here is that "electricity" is not really a
well-defined thing. The article you reference states that "the word 'electricity' refers generally to the movement of electrons (or other charge carriers) through a conductor."
However, air is not a conductor and the electrons are not free to move.
Therefore there is no electric current in air and therefore no electricity.
In a conductor, the electrons move because they experience an electric field
(I find the reference to the electromagnetic wave in your reference to be
actually inaccurate.) Before the "switch is closed" there is no electric
current (electricity) because there is no electric field. When the switch is
closed, the electric field has to establish itself in the conductor and this
field is set up at approximately the speed of light. The speed of light is
air is, for all intents and purposes the speed of light; there is, however,
as I have said, no "electricity" in the air.
 NOTE
ADDED:
NOTE
ADDED:
If the electric field is strong enough, the electrons will be
ripped off the air molecules and a current will flow. This is what lightning
is. I do not think that is what you are interested in, though.
 QUESTION:
QUESTION:
i have heard several times that the gravitaional attraction of the sun provides the centripetal acceleration for the planets to revolve around the sun. but why is it not that the planets are directly accekerated towards the sun linearly and they fall into the sun? why do they revolve only?
 ANSWER:
ANSWER:
There are two ways that acceleration, in response to a force,
can happen. The magnitude of the velocity vector can change or its direction
can change. If an object is in a perfectly circular orbit, only its
direction changes and its speed stays the same. If an object is simply
dropped, only its speed changes. Any other situation will result in both
direction and magnitude of velocity changing. No planet has a perfectly
circular orbit, all are in slightly eliptical orbits. But, they are nearly
circular and it is a pretty good approximation to say that the force changes
the direction but not the speed of the velocity.
Newton's mountain
may help you to understand this.
 QUESTION:
QUESTION:
How much buoyancy does 1 cubic foot of vacuum have at sea level?
 ANSWER:
ANSWER:
The buoyant force is the weight of the displaced air. The air
has a density of 1.225 kg/m3. 1 ft3=0.0283 m3, so the
mass of the displaced air is m=1.225x0.0283=0.0347 kg. The weight is
then mg=0.0347x9.8=0.34 N=0.0764 lb.
 QUESTION:
QUESTION:
How long would it take for a 50lb solid steel sphere to sink a quarter mile through ordinary water?
 ANSWER:
ANSWER:
I will assume that the sphere quickly reaches terminal
velocity so that I can assume that it goes the whole quarter mile with that
constant speed. This should be an excellent approximation. The terminal
velocity may be written as vt=√[2mg/(ρACd)]
where m is the mass, g =9.8 m/s2 is the acceleration due to
gravity, ρ is the density of water (1000 kg/m3), A is the
cross sectional area of the sphere, and Cd is the drag
coefficient which is 0.47 for a sphere. There is one catch here, that this
is without buoyant force and the buoyant force in water is equal to the
weight of the displaced water which is not negligible here; when it comes
time to put in the mass I will put in an effective mass of the mass of the
steel sphere minus the mass of an equal volume of water. I will work in SI
units, so 50 lb=22.7 kg and 0.25 mi=402 m. The density of steel is 7850 kg/m3
so the volume occupied by 22.7 kg is V=22.7/7850=0.0289 m3;
the radius of a sphere with this volume (using V=4πR3/3)
is R=0.0884 m and so the area (using A=πR2)
is A=0.0245 m2. Finally, the effective mass would be m=22.7-1000x0.0289=19.8
kg. Putting all these into the equation for vt, I find vt=5.81 m/s. The time an object going this speed takes to
travel 402 m is 402/5.81=69 s, 1 minute and 9 seconds.
 QUESTION:
QUESTION:
Suppose that the Death Star was stationary and aiming its laser at a relatively small moving space craft, like a Space Shuttle, and there was enough distance between them so the Death Star had to lead the shot. Would another space craft flying by at close to the speed of light see the laser miss while the people in the Death Star would see a hit, since the speed of light is constant, and the shot will travel faster according to the observers in the craft flying by, and will reach the intended target location before that Space Shuttle gets there?
 ANSWER:
ANSWER:
You make a contradictory statement: "since
the speed of light is constant, and the shot will travel faster according to
the observers in the craft flying by". If the speed is constant, how can it
travel faster? In fact, all observers will agree that the shuttle will be
hit. Two observers cannot disagree on an event which happens in one frame;
they can only disagree on things like "where" and "when" the event happened.
 QUESTION:
QUESTION:
Premise: an airplane can only fly so high because of aerodynamics (low air pressure/no oxygen to burn). Question: if these limitations didn't exist, could it continue to climb altitude and reach "space" thus without reaching or exceeding escape velocity?
 ANSWER:
ANSWER:
Certainly. See an
earlier answer.
 QUESTION:
QUESTION:
I just watched a documentary about the history of nuclear weapons and it said that 100 megatons is the maximum ''practical'' yield for a nuke because if it gets bigger than that, the fireball will be larger than thickness of the majority of the atmosphere and therefore most of the effect of the nuke will escape to space making bombs larger than 100 megatons redundant as an idea. Can you confirm this?
 ANSWER:
ANSWER:
No, I cannot confirm this because it does not make sense to
me. The fireball of the largest bomb ever detonated, 50 Mt, had a radius of
about 2.3 km. I estimate that a bomb with twice that energy would have a
radius about 3√2=1.26 times bigger, 2.9 km. Airplanes fly at an
altitude of about 30,000 ft=9.1 km and there is certainly enough atmosphere
there for an airplane to fly. And, even if most of the atmosphere was gone
at 3 km, why would that imply that "most
of the effect…will escape to space"? The blast also does a lot of damage
beyond the fireball at ground level which would increase with the yield of
the bomb, and that is where you want to do damage. It is my impression that
the reasons for not developing larger bombs are tactical: the heavier the
bomb, the more difficult it is to deliver it.
 QUESTION:
QUESTION:
In a 20 X 20 room you have a movie projector on the east side with a screen on the west wall. On the south side you have another projector with a screen on the north wall. What happens to the pictures on the screens when the two projector beams cross at a 90 degree angle. Do the pictures remain cohesive or are they distorted? What is happening in the convergence zone where the beams are crossing? In this instance is light acting as a wave or particle?
 ANSWER:
ANSWER:
Light waves obey an equation which is linear; what that means
is that when two waves pass the same place the net amplitude of light is
equal the the sum of the two individual amplitudes. In your case, what this
means is that the light from one projector passes right through the light
from the other unaffected. Wave or particle? It depends on what you are
looking for. The light, just like all electromagnetic radiation, is both
waves and particles. (This does not mean a mixture.)
 QUESTION:
QUESTION:
A plumb bob is hung from the ceiling of a train compartment. If the train moves with an acceleration 'a' along a straight horizontal track, the string supporting the bob makes an angle with the normal to the ceiling whose tangent is 'a/g'. Suppose the train moves on an inclined straight track with uniform velocity. If the tangent of angle of the incline is 'a/g', the string again makes the same angle with the normal to the ceiling. Can a person sitting inside the compartment tell by looking at the plumb line whether the train is accelerated on a horizontal straight track or it is going on an incline with uniform velocity? If yes, how? If no, is there a method to do so?
 ANSWER:
ANSWER:
First you should carefully read an earlier answer on the
accelerated pendulum. (Actually, I see that you
are the person who asked that question!) To answer your question, you can't
tell by "looking" but you certainly can tell by measurements. For example,
in the accelerated problem the tension in the string is m√(g2+a2);
for the inclined track the tension is mg. Or, in the accelerated
problem you feel youself being pushed back with a force (fictitious) Ma,
but on the inclined track you feel yourself being pushed back with a force
(real) Mgsinθ=Mg[a/√(g2+a2)].
 QUESTION:
QUESTION:
Is it possible, and if so how to calculate the magnitude of a 4-dimensional vector?
 ANSWER:
ANSWER:
I assume that you are asking about 4-vectors in special
relativity. This kind of question can depend on the mathematics of the
multidimensional coordinate space you are working with, but in special
relativity if a vector has a space-like part (Ax, Ay,
Az) and a time-like part A
t,
then the magnitude of the vector is A=√[At2-(Ax2+Ay2+Az2)].
For example, the space-time vector has a magnitude of R=√[c2t2-(x2+y2+z2)]=√[c2t2-r2]
and the energy-momentum vector has a magnitude of √[E2-(px2+py2+pz2)c2]=
√[E2-p2c2]=m0c2.
If you want a bunch more detail, see the Wikipedia article on
4-vectors.
 QUESTION:
QUESTION:
why air is a bad conductor? why lightning occurs even if the air is a good insulator?
 ANSWER:
ANSWER:
Gases are almost always poor conductors because there are no
electrons to carry the current. If the electric field in a gas gets strong
enough, electrons will be pulled off the atoms allowing current to flow. In
addition, the electrons which are freed will smash into other atoms in the
gas causing more electrons to be knocked off atoms; this is called cascading
and happens any time there is a spark in a gas (of which lightning is an
extreme example).
 QUESTION:
QUESTION:
what would happen if someone were to HOLD the gun and shoot it. The person would not be tethered to anything and would be floating freely in space. If that person is around 160Ibs and shot a High power rifle how fast would it project the wielder in the opposite direction? I know it wouldnt be as fast as the bullet because of the mass of the person but I'm curious to what extent they would be projected into space... if thats would even happen at all.
 ANSWER:
ANSWER:
First, read an earlier answer to a
question similar to yours. The concept you want to use here is momentum conservation.
Momentum is the product of mass times velocity and the total momentum of
a system must be the same before and after the gun has fired. The mass
of a 160 lb man plus his gun is about 75 kg, the mass of a typical bullet is
about 0.015 kg, and the muzzle velocity of a high-power rifle is about 250
m/s. So, since the momentum is zero before the rifle is fired, 0=75v-250x0.015=75v-3.75
or v=0.05 m/s which is about 10 ft/min.
 QUESTION:
QUESTION:
We have a kitchen table that is extremely heavy and we know of no way to
weigh it. If I put one leg on a scale, it reads 143.2 lbs. I'm thinking
we can't simply multiply that number by four because it seems it may
register some of the weight from at least part of the other three
quarters.
 ANSWER:
ANSWER:
Get a 2x4 which will span the two legs at one end and weigh
it; call that weight w. Put the 2x4 under the legs at one end and the
scale under that; the scale will read W1. Move the 2x4 and
scale to the legs at the other end; the scale will read W2.
The weight of your table is W=W1+W2-2w.
If your table is symmetrical, you will find W1 to be about
the same as W2.
 QUESTION:
QUESTION:
what dose " 3.37500000E+15MPH" mean ?
 ANSWER:
ANSWER:
It means that you travel 3,375,000,000,000,000 miles in each
hour. It is, however, an impossible speed since the speed of light is 6.7x108=670,000,000
mph and nothing can travel faster than the speed of light.
 QUESTION:
QUESTION:
I work with autoclaves, my question is what would happen if a person got trapped in an pressure vessel and the autoclave was pressured to 3 pounds (this is the normal pressure value after the door is locked)?
 ANSWER:
ANSWER:
For the benefit of readers who do not know what an autoclave
is, it is a sterilizing chamber using high-temperature steam (~1200C)
at high pressures. Pressure is measured in pounds per square inch (PSI) and
atmospheric pressure is about 14.7 PSI. So, I assume your 3 pounds is 3 PSI
above atmospheric, called the gauge pressure. So the added pressure would be
about 20% above normal. When you go under water, about 30 ft, you experience
about 100% above normal, double the normal atmospheric pressure, and you
know you can do that with no ill effect. So, essentially what would happen
in your scenario is that you might feel a little pressure in your eardrums
but not much else.
 QUESTION:
QUESTION:
A rigid container filled with air is placed in vacuum. If a small hole is created on one side of the container, air leaks out and the container moves in the opposite direction. How would the container move if the situation were reversed, i.e. a rigid container of vacuum placed in air with a hole on one side of the container? I can't seem to apply Newton's 3rd law and momentum conservation to solve this convincingly.
 ANSWER:
ANSWER:
Let's just think of a cubical box with a hole in one face.
Any molecule which finds the hole will enter the cube, go to the opposite
face, collide with it, and rebound, thereby transferring some momentum to
the box. The box is now moving in the direction in which the molecule was
originally moving (I will call that the forward direction). The rebounding
molecule will either go back out the hole or hit inside the cube and bounce
back again. As long as the molecule stays inside the box, the net effect
will be zero but eventually it will find the hole and so the net effect will
be one collision moving the box in the forward direction. Now think of a
huge number of molecules entering the hole. At the beginning, more will be
coming in than going out so the net force on the box will be forward.
Eventually, there will be the same density of molecules inside and outside
the cube so the net force will become zero. Bottom line—the cube moves in
the same direction as if air were being released from it. An intuitive way
to see this is to note that each entering molecule carries a momentum in the
forward direction, so that is the momentum available to be transferred to
the cube.

 QUESTION:
QUESTION:
From a physicist's point of view do you ever see us using antimatter as an energy source and are there any ways to even theoretically to create antimatter in adequate quantities? Is antimatter power really just a theoretical thing that won't get any practical use in your opinion?
 ANSWER:
ANSWER:
So, you have to ask yourself where you are going to get this
antimatter. You have to make it because there is never any appreciabale
amount just sitting around. You can be sure that it would cost you more
energy to create it than you would get from annihilating it.
 QUESTION:
QUESTION:
If electrical currents are charged particles, then electricity must be composed of matter (obvious.....I think) if that were the case, then our thoughts, dreams, etc, are simply a result of charged neurons interacting within our synapses through electrical currents.
So, I suppose my question is, if our are thoughts are confined to ourselves or do they hold a place within the whole concept of time and space.
 ANSWER:
ANSWER:
Certainly, brain activity involves electric currents.
Electric currents create electromagnetic fields which can be detected
outside of you, so brain activity is not "confined to ourselves."
Neuroscience researchers routinely sense these fields with detectors outside
the subjects. If you are suggesting a possible explanation for ESP, I sure
would not bank on it. As far as we know, our brains are good at creating
very weak fields but not at detecting very weak fields. Also, there is
presently no known way of actually interpreting the thoughts which caused
those fields.
 QUESTION:
QUESTION:
A photon is created when an electron returns to its original energy state (I think). How/when does a photon die? Does it die? Does it run out of energy?
 ANSWER:
ANSWER:
Atomic or molecular transitions do, indeed, create photons.
There are many other ways to create them—radio broadcasting antennas, for
example, spew them out by the jillion. A photon carries energy, so the only
way it could "die" or "run out of energy" would be to give its energy to
something else. When you look up into the heavens at night, you see photons
which have been traveling millions or billions of years to get here, so they
evidently never die if they never interact with something else. Here are a
few ways photons can lose energy:
-
If a photon encounters an atom like the one that
made it, the photon can excite the electron up to the higher state
again, thereby disappearing.
-
If it encounters an electron, the photon can
give the electron all its energy; this is called the photoelectric
effect.
-
If it encounters an electron, the photon can
scatter from the electron thereby losing part of its energy; this is
called the Compton effect.
-
If it has enough energy, it can interact with
the electric field of an atomic nucleus and spontaneously create an
electron-positron pair; this is called pair production.
The bottom line is that photons must find something
to interact with or else they will live (as far as we know) forever.

 QUESTION:
QUESTION:
Would it be possible to have flying cars in rotating space habitats or would it be really difficult to fly them? And I want to thank you for making this incredibly awesome site for people with questions regarding physics.
 ANSWER:
ANSWER:
Have you read Larry Niven's sci-fi book Ringworld? It
is about a rotating space habitat. I recently analyzed
"free fall" in such a world. If you want to understand the details you
should read through this carefully. Interestingly, as long as the radius is
very large, a projectile would move very similarly to how it would move in a
gravitational field. However, there is a profound difference, namely that
when in the air, there is no force on the projectile. This would make flying
anything different from on earth, but I suspect the skill to do so would be
pretty easily acquired.
 QUESTION:
QUESTION:
If the earth was to just vanish disappear without a trace what would
happen to the moon?
 ANSWER:
ANSWER:
The details depend on exactly where the moon was in its
orbit, but the simple answer is that it would go into an orbit around the
sun.
 QUESTION:
QUESTION:
why do we say that materials in our world are mostly empty space
 ANSWER:
ANSWER:
The simplest way to think about atoms is to have little
electrons in orbits around the nucleus. The nucleus is extremely small
compared to the size of the atoms and electrons have a tiny mass compared to
the nucleus. Therefore, like you would say that the solar system is composed
mostly of empty space, you would say that the atom is composed of mostly
empty space. The reality is, though, that the elctrons are really smeared
out over the whole volume of the atom, they are like a cloud rather than
like little planets, so the atoms are not really empty space.
 QUESTION:
QUESTION:
from where do elements heavier than hydrogen originiat
 ANSWER:
ANSWER:
See an earlier answer.
 QUESTION:
QUESTION:
There is a demonstration where a person is put in a trashbag and the air vacuumed out. The person can't move their arms. Is this because of the pressure difference between the inside and outside of the bag, or because of the large surface area of the bag allows them to feel more pressure?
 ANSWER:
ANSWER:
There are two things going on here. First, it is like being
tied up, the bag restrains you. If you were shrink-wrapped you would also
not be able to move. But, the trash bag is bigger than you so it would not
be "tied up" by it because it would be like a loop rope which was 5 feet in
diameter. However, when the air in the bag is removed, the atmospheric
pressure on the outside holds the bag tightly to you and it becomes just
like shrink-wrapping. Here is a
you-tube video (you
can find lots of others).
.jpg)
 QUESTION:
QUESTION:
I have a question about force on a lever. I am building a set of oars
for a whitewater raft. The industry is full of opinions but very few
physicists. We all agree that the force is greatest at the oar lock
(fulcrum) but nobody has any idea how much less force is present at the
neck (the narrow part just above the blade). If you will do this
one...here are the values. Using a 10' oar the fulcrum is at the 32-36"
mark and the neck is at the 90" mark. The blade occupies the remaining
30". We taper the oars knowing they don't need to be as strong away from
the fulcrum but nobody knows how much we can taper because we don't know
how much less force they need to withstand. The taper results in the
neck having anywhere from 65% to 80% of the wood on the shaft. I suspect
80% is overkill. Any thoughts.
 ANSWER:
ANSWER:
A disclaimer: I am not an engineer and an engineer would
probably be a better person to ask this question. When you are rowing, the
water exerts a force, call it F, on the blade of the oar. I am
thinking that the thing we should be thinking about is the torque which this
force exerts about the lock compared to the torque it exerts on the neck.
This force may be thought of as being 15" from the neck, approximately in
the middle of the blade; so the torque from the water force at the neck
would be 15F. The torque at the lock would be, assuming the lock is
35 inches from the handle, about 55"; so the torque from the water force at
the lock would be 55F. So the torque on the lock would about 55/15
≈3.7
times bigger than the on the neck. Now we get into some pretty complicated
materials engineering, see this
link.
It turns out that the stress σ is inversely proportional to a
quantity Z called the section modulus. For a cylindrical shape of
radius R, the section modulus is Z=0.78R3.
So, I surmise that an estimate of how much smaller the neck would be than
the lock would be Rneck3/Rlock3≈1/3.7
or Rneck≈0.65Rlock, about 2/3 the
thickness.
 QUESTION:
QUESTION:
If I have a ramp that is 28 feet long, fixed at the upper end (shore) and weighs 400 lbs that has a 6 foot rise, how do I calculate the weight at the lower end (dock)? I am trying to determine how much floatation I need under the water end to support the weight of the ramp at that end. That rise varies during the course of the year from zero feet to a maximum of 7 feet.
 ANSWER:
ANSWER:
I am assuming that the ramp is a uniform plank, that is, that
its center of gravity is at its geometrical center (14'). Refer to the
picture on the left. Two equations must be satisfied for equilibrium, the
sum of all forces must equal zero and the sum of all torques about any axis
must be zero. The first condition gives us that F1+F2-400=0
and the second condition (summing torques about the center of the ramp)
gives us that F1-F2=0. Solving these two
equations, F1=F2=200 lb. Note that the
answer, 200 lb, is independent of the rise.
 QUESTION:
QUESTION:
Two dice are suspended in outer space with no visible forces acting on them. Their center of masses are 10 cm apart, and they each have an identical mass of .0033 kg. How long would it take for the force of gravity between them to cause them to touch? (We will assume they are volumeless for more ease in calculation).
 ANSWER:
ANSWER:
This seems a very difficult problem because the gravitational
force between them changes as they get closer and so it is not a case of
uniform acceleration. However, this is really just a special case of the
Kepler problem (the paths of particles experiencing 1/r2 forces) which I
have done in detail
before.
You can go over that in detail. For your case, K=Gm1m2=6.67x10-11x(3.3x10-3)2=7.26x10-16
N∙m2, the reduced mass is
μ=m1m2/(m1+m2)=0.0033/2=1.65x10-3
kg, and the semimajor axis
a=2.5
cm=2.5x10-2 m. Now, from the earlier
answer, T=√(4πμa3/K)=5.98x104
s. The time you want is T/2=2.99x104 s. This is only 8.3
hours and seemed too short to me. To check if the time is reasonable, I
calculated the starting acceleration and assumed that the acceleration was
constant and each die had to go 5 cm; this time should be longer than the
correct time because the acceleration increases as the masses get closer.
The force on each die at the beginning is K/r2=7.26x10-16
/0.052=3.04x10-13
N; so, the resulting initial acceleration is F/m=3.04x10-13/3.3x10-3=9.21x10-11
m/s2. So, assuming uniform acceleration, 0.05=½at2=4.61x10-11t2.
Solving, t=3.3x104 s. So, the answer above is, indeed,
reasonable.
 QUESTION:
QUESTION:
If we can talk about "escape vel. for light ,(in case of black holes)"
that mean light is affected by gravitational fields and thus like other
masses, must be "decelerated", while moving away from a heavy planet.
Thus, can we slow down light to near zero speed? I know the ans is 'no',
but WHY? if light is affected by gravity then we should be able to slow
it down? Also if light is affected by gravity , then what's it's mass??
 ANSWER:
ANSWER:
As light travels upward in a gravitational field, it
loses energy. If light were a classical object like a baseball, you
would say that, since its energy is ½mv2 and
the mass is constant, the velocity must decrease. However, the energy of
light, since it has no mass, is not ½mv2 but rather each photon has an energy hf where
h is Planck's constant, and f is the frequency of
the light. So, as it goes higher its frequency gets smaller—the wavelength
gets longer; that is why it is called gravitational red shift. In the
case of a black hole, eventually the energy of the light is zero and the
black hole has gained all the energy which the light had. Similarly, if
light is aimed down in a gravitational field it does not speed up but rather
increases frequency as it goes down, gravitational blue shift. Light
does not have mass but it is affected by gravity. Newton's universal law of
gravitation is not the last word; the modern theory of gravity is general
relativity and if you go to my FAQ
page you can learn about how gravity affects massless objects.
 QUESTION:
QUESTION:
My physics teacher has taught us that people who are going to travel in an aeroplane should empty ink from their pens as if ink is filled at high pressure at the ground level, it will leak out when the plane flies in the low pressure. But the plane is air-tight. How can low pressure act from outside the walls of the plane? Also, does the density of the ink changes when we carry to low-pressure region?
 ANSWER:
ANSWER:
The inside of an airliner is pressurized, but not to
sea-level atmospheric pressure. The pressure is typically about the same as
the pressure at an altitude of 2100 m, approximately 80% of sea-level
pressure. Ink is mostly water and water is essentially incompressible, so
the density does not change.
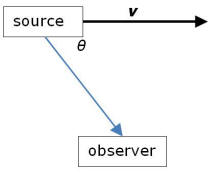
 QUESTION:
QUESTION:
Is there a Doppler shift between the centre and outside of a wheel.
Say for example a standard merry go round you find at a sideshow, if I stand in the middle and look at something on the outer does my image Doppler shift.
The reason it is confusing to me is because your angular rotation is the same for both people but not your linear speed.
 ANSWER:
ANSWER:
If you were asking about sound rather than light, there would
be no Doppler shift because for normal waves there is no effect if there is
no component toward or away between the source and the observer. For light,
however, which is what you ask about, there is a Doppler shift. If your
question had asked for a source and and observer moving on straight parallel
paths with different speeds (sort of what you asked), then you could
relatively compactly write the Doppler shift equation relative to the
observer. In the figure to the right, the observer will see the source
moving with a speed v and light comes at an angle θ as shown.
In this case, f'=f/[γ(1+(vcosθ/c))] where
γ=1/√[1-(v2/c2)] and
f and
f' are the frequencies at the source and observer, respectively. If
θ=900,
f'=f/γ; this is called the transverse relativistic Doppler
effect. But, in your scenario, each will see the other to be at rest. But
both are actually accelerating relative to an inertial frame, so the
situation is not so simple. You can see a discussion of this scenario on
Wikepedia. Suppose that the source is at a distance
r1
from the center, the observer is at a distance r2, and the
angular velocity is ω. Then assuming that the
distance traveled by the observer in the time it takes the light to travel
between the two is very small, I find that f'≈f√[(1-(r1ω/c)2)/(1-(r2ω/c)2)].
I just realized that you actually asked an easier question, namely that r2=0
and r1=R where R is the radius of the
merry-go-round, so, f'=f√(1-(Rω/c)2). This is
exactly the same as the transverse Doppler effect above, f'=f/γ.
[Sorry that the answer is much longer than needed. Whenever I misread a
question and do a lot of interesting and more general work, I am loathe to
delete it! The concise answer for you is that f'=f/γ.]
 QUESTION:
QUESTION:
I have a question concerning a magnet suspended inside a copper tube. Does the copper tube accumulate the mass of the magnet? In other words, does the copper tube now weigh more with the magnet suspended in the middle? or is it partial weight because the magnet does fall inside, albeit slowly.
 ANSWER:
ANSWER:
First, some terminology. Weight is the force which the earth
exerts on something, so the weight of the copper tube is always the weight
of the copper tube. If a magnet falls through a copper tube, it induces
currents in the copper and these currents exert a force on the magnet which
tends to slow it down. In fact, the force becomes strong enough that the
magnet quickly reaches a terminal velocity—it falls with a constant speed.
That means that the tube is exerting an upward force on the magnet equal to
the weight of the magnet. But, Newton's third law says that if the tube
exerts a force on the magnet, the magnet exerts an equal and opposite force
on the tube. Therefore, if the tube is standing on a scale, the scale will
read the weight of the tube plus the weight of the magnet, but that does not
mean that the tube got heavier. It is just the same as if you put the tube
on the scale and pushed down on it with a force equal the weight of the
magnet; you would not say that the tube got heavier because you pushed on
it. A good demonstration of this can be seen at
this link.
 QUESTION:
QUESTION:
I was curious to know how the kinetic energy a water balloon endures when free falling affects the radius of it's splatter.
 ANSWER:
ANSWER:
So, you are wondering what the radius of the splatter depends
on and how? Of course, to do an accurate calculation would be neigh on
impossible. I will just do a very rough approximation and then you
can do an experiment and see if it makes any sense. At the instant that the
water baloon hits the ground its kinetic energy is K=½MV2=Mgh
where M is the mass of the water balloon, V is the speed it is
going, h is the height from which it was dropped, and g is the
acceleration due to gravity. Suppose that most of the energy of the water
ends up as kinetic energy of the droplets in the splash and that the splash
is made up of N drops all the same size, mass m and speed v
each. Then the kinetic energy of the splash is ½Nmv2=½Mv2=Mgh.
In other words, the speed of each drop is the same speed as the balloon had.
Therefore the speed of each drop of the splash is v=√(2gh).
Now, the radius of the splash will surely be proportional to the speed of
the drops, R~√h (read "R is proportional to the square
root of h"). So my prediction is, for example, that if you drop it
from 8 m the splash will be about twice the size as if you drop it from 2 m.
This, as I said, is very rough. If you try to check it, let me know. (In
answer to your question, the kinetic energy does not "endure" since
eventually everything comes to rest. When I assume that the kinetic energy
is approximately conserved in the splash, I am talking about immediately
after the balloon hits.)
 QUESTION:
QUESTION:
Why do we divide by rsquare in coulomb's law and what is the role of 4pie in the constant of proportionality in the coulomb's law.
I am not able to understand as to why we divide the product of q1*q2 by 4 pie rsquare.
 ANSWER:
ANSWER:
The reasons for r2 and 4π are
different. Coulomb's law is a statement of an experimental fact. If you have
two charges, q1 and q2, and measure the
force F they exert on each other and then double either charge, the
new force will be twice as great; you have therefore found out experimentally that
F~q1 and F~q2
(~ means "is proportional to"). Now, if you keep the charges constant and
double the distance between them you will find that the force gets 4 times
smaller; you have therefore found out experimentally that F~
1/r2.
(Of course you would also do many other similar measurements like tripling
the charges or halving the distance etc.) Putting it all together,
Coulomb's law tells you that F~q1q2/r2.
But we usually prefer to work with equations rather than proportionalities,
so we introduce a proportionality constant k: F=kq1q2/r2.
The usual way to determine k is to measure F for a particular
q1, q2, and r. [Note that the SI
unit of charge, the Coulomb (C), is defined independently of Coulomb's law;
it is defined in terms of the unit of current, the Ampere (A), 1 C/s=1 A.]
You find that k=9x109 N∙m2/C2.
Another way to put it is that you would find that two 1 C charges separated
by 1 m will exert a force of 9x109 N on each other. That answers
your first question about why the 1/r2 appears in
Coulomb's law—it is simply an experimental fact, it is the way nature is.
Your second question is why do we often see the proportionality constant
written as k=1/(4πε0). There is nothing profound
here; later on when electromagnetic theory is developed further, choosing
this different form leads to more compact equations. Essentially, many
equations involve the area of a sphere which is 4πr2 which
means that there would be many factors of 4π floating around in your
equations of electromagnetism if you used k as the proportionality
constant.
Since I often think of
physical laws in terms of proportionalities, as I did above, I include here
another way this could have worked. Maybe you are content with the answer
above and can just ignore this! We could have used Coulomb's law to define what a unit of charge is. Having done the experiment and
determined that F~q1q2/r2,
we could have chosen the proportionality constant to be 1.0 if we wished to
define what a unit of charge is: F=q1q2/r2.
Now, 1 unit of charge would be that charge such that when two such charges
are separated by a distance of 1 m, the force each experiences is 1 N; that
new unit of charge would have been 1 kg1/2∙m3/2/s=1.054x10-5
C. In fact, if you do this in cgs units instead of SI units, where F
is measured in dynes (gm∙cm/s2) and r is measured in cm,
the unit of charge is called the statCoulomb (statC) and 1 statC=√(1 dyne∙cm2)=√(1
gm∙cm3/s2)=1 gm1/2∙cm3/2/s=3.34x10-10
C. Personally, I think this is a more logical way to define electric charge,
but often history demands that we use the long standard definitions of
units; in the case of electric charge, the ampere, not the coulomb, is taken
as the fundamental unit.
 QUESTION:
QUESTION:
if i put a half of Hollow tube insid the water(and the other half is in the
air) and drop to it a coin - it will sink.
now if i put from the top of the tube a coin that fit the Diameter of the
tube and water cant pass this coin what will happen?
 ANSWER:
ANSWER:
When the coin first touches the water, there will be its own
weight Mg down acting down on it, the atmospheric pressure force PAA
acting down on it (A is its area), and the atmospheric pressure force
PAA of the surface of the water acting up on it.
Hence the net force will be Mg down and it begins to sink. However,
after it has sunk to a depth D the pressure up from the water has
increased by an amount ρgD where ρ is the density of the
water. So now, Ma=-Mg-PAA+(PAA+ρgDA),
or a=-g+ρgDA/M. If the water caused no drag on the coin as it
fell (obviously not correct), the coin would oscillate about the equilibrium
depth De=M/(ρA) with simple harmonic
motion. In the real world, there would be some drag forces and the coin
would eventually come to rest at De.
 QUESTION:
QUESTION:
If I had one quarter made out of matter and another quarter made out of antimatter using the formula E=MC� how big would the explosion be?
 ANSWER:
ANSWER:
The mass of a quarter is m=5.67x10-3 kg. The speed
of light is c=3x108 m/s. Doing the arithmetic, E=2mc2=1.02x1015
J. That is about 10 times the energy of the Nagasaki atomic bomb.
 QUESTION:
QUESTION:
i'm trying to understand black body radiation, i've heard that "every object at a finite temperature radiates light" and my question is, why is it specified 'finite temperature'? isn't that kind of redundant? is there any object that has infinite temperature?
 ANSWER:
ANSWER:
Often "finite" is incorrectly used to mean "nonzero"; I would
say that is the case here. Temperature is a measure of average energy per
particle, so, to a first approximation there is no upper limit to
temperature. However, there is not an inifinite amount of energy in the
entire universe, so the temperature does have an upper limit depending on
how much energy the universe contains.

 QUESTION:
QUESTION:
So I'm a high school student who studies advanced physics and calculus in my free time. Across my study Of three dimensional graphing I came across equations that use t as variable along with an f(x,y) and the graphs move and change. What kinds of equations are these and where can I find them.
 ANSWER:
ANSWER:
There are innumerable examples of equations of this sort. I
will give one example: a vibrating drum head. Shown to the right is a drum
head vibrating with its lowest possible mode. The equations I will write are
valid only for x2+y2≤R2
where R is the distance from the center of the drum to the rim and
the origin is at the center. If it is not vibrating, the drum may be
represented as z=f(x,y,t)=0 where z is the third
dimension perpendicular to the plane of the drum head. When it is vibrating
in the mode shown, at the time when the center of the head is farthest from
z=0, the shape may be described as z(x,y)=z(r)=Acos[πr/(2R)]
where r=√(x2+y2); note that
z(0)=A
and z(R)=0. Finally, let the drum vibrate sinesoidally by
replacing A by Asin(2πft) where f is the
frequency (vibrations per second): z(r)=Asin(2πft)cos[πr/(2R)].
[The actual solutions for z(x,y) are mathematical functions
called Bessel functions, not sinesoidal functions, but that is beyond high
school level mathematics. My example is an adequate approximation.]
 QUESTION:
QUESTION:
If energy can neither be created nor destroyed, how can people who believe in the bing bang believe what they believe since we have energy now so they are saying that it was created by something in the natural world which we know is not possible.
 ANSWER:
ANSWER:
The law of conservation of energy applies only to our
universe after its creation. Nobody knows where the original energy came
from for the "bing bang". I should also point out that energy conservation
can be violated in nature; the Heisenberg uncertainty principle allows
energy to appear out of nothing but only for short times.
 QUESTION:
QUESTION:
Suppose a constant force is acting on an particle, due to which the particle is accelerated. The the velocity of the particle is increasing at a constant rate. Now if I use the relation P=F.v, i get the power delivered to the particle different at different instants since the velocity is different at different instants. But it is difficult for me to digest that though the force applied is constant, the power goes on increasing. Am I thinking right?
 ANSWER:
ANSWER:
What is power? It is the rate of change of energy. In the
example you give, a constant force in one dimension, the energy at any
instant is ½πmv2. Just to illustrate, let's let m=2
kg, a=1 m/s2, and the mass begins at rest at t=0.
After the first second, E1=½x2x12=1 J; after
the second second, E2=½x2x22=4 J; after the
third second, E2=½x2x32=9 J; after the fourth
second, E2=½x2x42=16 J; etc. So, the
average power delivered over the first second is ΔE/Δt=(1-0)/1=1
W; the average power delivered over the second second is ΔE/Δt=(4-1)/1=3
W; the average power delivered over the third second is ΔE/Δt=(9-4)/1=5
W; the average power delivered over the fourth second is ΔE/Δt=(16-9)/1=7
W; etc. The reason you are not "thinking right" is that you deliver
more energy to a faster-moving object with a given force over a given time
because energy is proportional to the square of the speed. Another way to
look at it is that average energy delivered by a constant force F
acting over a distance Δ
x
is ΔE=FΔx but, in any
given time, the force acts over an ever-increasing distance adding an
ever-increasing amount of energy; of course, that is where your power
equation comes from, P=ΔE/Δt=FΔx/Δt=Fv.
 QUESTION::
QUESTION::
You have devoted your professional life to Physics and have known or worked with some very bright people. I wondered what you think sets some (Telsa, Newton, Einstein, et al) apart?
Just being smart is not enough as there are many smart folks out there. I've knew a few @ Florida that scored 1600 of 1600 on SAT
& a few @ P&G over the years.
Is it how they think about things, imagination as Einstein said, or what? Wondered what you thought.
 ANSWER:
ANSWER:
Have you read the book
Outliers by Malcolm Gladwell? It presents examples of what I consider to be an important component of success—serendipity of circumstances. Here is how this may have helped Einstein and Newton:
-
Newton was at Cambridge when it was closed down because of the Great Plague in 1665. He went to the family home and had two years for private study during which he laid the foundations of his theories of gravity and optics and his invention of the calculus.
-
Einstein was not able to get an academic position and his position at the Swiss Patent Office was so trivial to him that he had plenty of time to develop special relativity, photoelectric theory, and get a good start on general relativity (see his recent
biography by Walter Isaacson).
Getting a 1600 on the SAT is no indicator at all, in my opinion. Both Einstein and Newton were famously very undistinguished students. Being in the right place at the right time and having an obsessive curiosity and posessing the willingness and imagination to think in new directions are much more important in my opinion.
 QUESTION:
QUESTION:
a raindrop falls at a
constant vertical speed of 1.6m/s in still air. the wind now blows
horizontally at 1.4m/s.
draw a scale diagram and use it to find the angle the path of the raindrop
now makes with the vertical?
 ANSWER:
ANSWER:
(I have been assured that this is not a homework problem, but
a problem on a test already given! It is not clear to me why the instructor
didn't provide a solution after the test.) What you are given is the
terminal velocity Vra of this raindrop, the
velocity of the rain (r) with respect to the air (a).
This is the speed it has in still air. But, in this problem, the air has a
velocity Vag
with respect to the ground (g).
But, you are on the ground and what you see is the velocity of the rain with
respect to the ground Vrg.
Using the velocity addition theorem,
Vrg=Vra+Vag.
As you can see from the diagram to the right, θ=tan-1(1.4/1.6)=41.20.
 QUESTION:
QUESTION:
why cant we hear the sound of vibrating electron of the house holding AC current though the frequency of the electron of house holding current is 50Hz that lies in the audible range. Also in case of transformer we hear the sound
 ANSWER:
ANSWER:
In a transformer, strong magnetic fields are caused by the
electric currents and these changing fields cause the whole the whole iron
core to vibrate causing audible sound (60 Hz hum). In household currents,
the fields are generally too weak to cause vibrations large enough to cause
audible sound. Even if the currents are relatively large, there are usually
no ferromagnetic materials nearby to respond to the fields.
 QUESTION:
QUESTION:
The book I am reading seems to be full of controversial sentences. One sentence reads " The sum of all electromagnetic forces between different particles of a system of charged particles is zero irrespective of the signs of the charges of the particles". Now how is that possible? For the resultant to be zero, don't we need half the particles positively charged and half negatively charged?
 ANSWER:
ANSWER:
There is nothing "controversial" about this, it is just
Newton's third law. Any isolated system has zero net force on it if all the
forces are internal (which is what "isolated" means in this context). If any
particle A has a force on it FAB because of the
presence of B, particle B has a force on it because to the presence of A
which is FBA=-FAB.
Just because the net force is zero does not mean that the system is static;
however, its center of mass is static (at rest or moves with constant
velocity).
 QUESTION:
QUESTION:
I've read about space habitat concepts for a while and I've ran into an interesting concept. The concept I've ran into is the McKendree Cylinder which is basically an O'Neill Cylinder made of carbon nanotubes. The O'Neill cylinder made of steel would be 32km long and 6km in diamter. The McKendree Cylinder would be 4600 km long and 460km in diameter. And the maximum length for MvKendree Cylinder is 10000km and diameter of 1000km. So McKendree one could be built a lot bigger than O'Neill one because the carbon nanotubes have greater endurance. But a habitat of thousands of km's seems to be really big when compared to what we can build from other materials. And as I recall we don't have any ways to produce Carbon Nanotubes in large quantities. Is it theoretically possible to build a habitat 10000km long and 1000 wide put of carbon nanotubes. And is the McKendree cylinder more of a theoretical design than a practical design that actually could be built?
 ANSWER:
ANSWER:
I presume that the issue is more a strength issue than
anything else. To illustrate how the strength of the material and its mass
determine the size the habitat can be, consider a rotating string of beads,
each of mass m. The rotation rate must be such that a=v2/R=g
where v is the tangential speed of each bead. Therefore each bead
must experience a force F=mg. This force can only come from the two
strings attaching each bead to its nearest neighbors and, from my drawing to
the left, F=mg=2Tsinθ. But, we will imagine many, many
beads on this string and we will call the distance between them d; so
we can make the small angle approximation that sinθ≈θ=d/R.
Solving for T, T=mgR/(2d). Now imagine that the beads
are atoms; d will be about the same for steel or carbon, g is
just a constant, msteel≈5mcarbon,
and the Young's modulus of carbon nanotubes is about 5 times bigger than steel,
Tsteel≈Tcarbon
/5.
So, Rcarbon/Rsteel≈(Tcarbon/Tsteel)/(mcarbon/msteel)≈25.
Your numbers are Rcarbon/Rsteel≈460/6=77;
I would have to say that my calculation is pretty good given that I have
made very rough estimates and I am not an engineer! I do not know what
considerations would limit the length of the habitat. (Of course, neither of
these models is presently practical to actually build, so call them
theoretical if you like. However, there is certainly no problem building
them if resources and manufacturing capabilities were available.)
 QUESTION:
QUESTION:
Dark Matter is a type of matter hypothesized to account for a large part of the total mass in the universe. In 1995 Hubble focused on a seemingly empty part of space only to find that it was filled with over 3000 visible Galaxies. My question is; why doesn't the Hubble Deep Field photo from 1995 make the existence of Dark Matter obsolete. If you were looking for the missing mass - its in the deep field photo.
 ANSWER:
ANSWER:
Finding more galaxies very far away does not solve the
problem of what I consider the most important evidence for something
missing, the internal dynamics of galaxies. The speeds of stars at different
distances from the centers of galaxies cannot be accounted for by the
gravity of the known normal mass distributions in the galaxies. Also, there
is a problem in cosmology as to when galaxies first started to form and when
we expected this formation to begin, again not related to total mass of the
universe. As I have frequently written here, my own feeling is that dark
matter is a hypothesis and it does not actually exist until it is directly observed; it may simply be that we do not understand gravity as
well as we think we do. Again I emphasize that I am not an expert in
cosmology and astrophysics.
 QUESTION:
QUESTION:
if both electric and magnetic components are absent in light what will happen
 ANSWER:
ANSWER:
That is like saying "if there were no atoms in my pencil,
what would it be?" Light is electric and magnetic fields and if
either were to disappear, it would not be light.

 QUESTION:
QUESTION:
when a body is weighted on an ordinary balance we demand that the arm should be horizontal if the weights on the 2 pans are equal.
Suppose equal weights are put on the two pans , the arm is kept at an angle with the horizontal and released.Is the torque of the two weights about the middle point(point of support) equal?(which i think, is). Is the net torque zero?. If so, then why does the arm rotate and finally become horizontal?
 ANSWER:
ANSWER:
I have gotten this question before and cannot answer it! The
balance to the left is in equilibrium if the balls are of equal weight and
the beam is uniform. I have searched the internet in vain trying to find the
details of a beam balance which cause it to be in equilibrium only if the
beam is horizontal. I can certainly imagine mechanisms which would
achieve this, but have not been able to find reference to what the mechanism
actually is. So, this is an appeal to all my loyal readers to come up with
an answer to question! (The balance on the right is a Roberval balance; its
purpose is to prevent the pans from tilting and, more importantly, to
balance regardless of where the weights are placed on the pans. It does not,
though, require that the beam be horizontal.)
 QUESTION:
QUESTION:
If you are driving at 60 mph and you slam on the breaks, you are accelerating?
 ANSWER:
ANSWER:
In physics, acceleration (a vector) means the rate of change
of the velocity vector. If you step on the gas, the acceleration is in the
direction of the velocity vector. If you step on the brake, the acceleration
is in the direction opposite the velocity vector. If you go around a curve
with constant speed, the direction of the velocity vector is changing, so
you are also accelerating.
 QUESTION:
QUESTION:
When a charged particle comes into existence from the decay of a neutral particle does the establishment of the associated electric field around the new particle constitute an electromagnetic wave? E.g when a neutron decays into a p, e and v I see nothing in the decay equation that includes the establishment of the p and e electric fields so am I right in thinking that the propagation of these new fields do not constitute electromagnetic waves?
 ANSWER:
ANSWER:
When a charged particle is created, an electric field is
simultaneously created. However, all space is not instantaneously filled
with that field but its existence propogates with the speed of light. So,
you will not know the particle is there until you can "see" it. Assuming
that the electron and proton move with approximately constant speeds after
the beta decay, there will be no electromagnetic radiation, just the
combined fields. They will also create magnetic fields because they are
moving.
 QUESTION:
QUESTION:
I have a question about fusion reactors. If the hot plasma in the reactor is contained in a magnetic bottle doesn't that shield us from receiving the heat to make power? How do we access the heat inside the magnetic bottle to use it to make power? What would happen if I tried to stick my hand into a magnetic bottle, would my hand penetrate?
 ANSWER:
ANSWER:
The magnetic bottle is just a magnetic field. You certainly
have no trouble moving your hand near a magnet where there is a magnetic
field. There is no reason why energy could not be transported out of the
magnetic bottle, it would just have to be carried by something with no
electric charge.
 QUESTION:
QUESTION:
A large jetliner traveling at 500+ mph hits a hollow, break away light pole....does it make a difference which of these two objects is moving and which is not, with regard to the damage?
My sense tells me, the plane would suffer some damage but it wouldn't be the same if it were the light pole were traveling/shot at the planes wing at 500+mph.
Doesn't the object with more momentum and mass usually win?
 ANSWER:
ANSWER:
If the pole were not attached to anything, it would not
matter which was moving. However, the light pole is attached to the plinth
on which it stands and therefore the moving plane would suffer more damage
than the stationary plane because more force is required to break the pole
away.

 QUESTION:
QUESTION:
when a coin moves around a fixed coin ,why it has to move two
times for a full round?( explain in mathematically ) the coins are surely the same size and one rolls on the other without slipping. you can try it by yourself.
 ANSWER:
ANSWER:
This is not really physics, but I will explain it. I do not
know about how "in mathematically" it will be, though. The coin is rolling
over a distance equal to its own circumference. If this distance were a
straight line, the coin would go through exactly one rotation, 3600.
However, the distance itself goes around 3600 also, so the
rolling coin undergoes a 7200 rotation, two full rotations.
 QUESTION:
QUESTION:
Is it possible to build an unsinkable ship by making the ship from materials less dense than water?
 ANSWER:
ANSWER:
It depends on what the ship carries. Obviously, for example, you could sink a wooden boat loaded with rocks.
 QUESTION:
QUESTION:
I want to run a 7.5kw generator for eight hours. I do know it takes 15hp to run a 7.5kw generator.
But I want to use weight to do it. Like a grand father clock. How much weight would I need to use if the weight could drop 6ft. ? I would like the equation or equations so I could choose to use more distance or use more weight to make this work for my application.
 ANSWER:
ANSWER:
So, what is 15 hp in SI units? 15 hp=11.2 kW; this makes
sense since some of the power is lost to things like friction. Your falling
weight must generate 1.12x104 J/s. If a mass m in kg falls
with some constant speed v, the power generated will be P=mgv
where g=9.8 m/s2 is the acceleration due to gravity. Now,
you stipulate that the time must be 8 hr=2.88x104 s, so if it
falls h meters in 8 hr, the speed would be v=h/2.88x104=3.47x10-5h.
So, P=mh∙9.8∙3.47x10-5=1.12x104=mh∙3.4x10-4;
so, your sought equation is mh=3.29x107 kg∙m. So, for
h=2
m (approximately 6 ft), m=1.65x107 kg
≈16,000
tons. You might want to rethink your plan! If you want to include the time
as a variable (in other words, wind your "grandfather's clock" more
frequently), the equation would be mh/t=1,140 kg∙m/s. (You
will need some kind of governor to regulate the speed and some gearing
system to ensure that the translational speed of the mass creates the right
rpm for the generator design.) I am afraid that a falling weight is not a
very good choice of power source for this application.
 QUESTION:
QUESTION:
Assume a small box, filled with small molecules, e.g.
hydrogen. The box is placed in a vastly larger box filled with bigger
molecules, e.g nitrogen. Pressure and temperature are equal at start. I
punch a tiny hole in the small box, so tiny only hydrogen molecules can
pass it. In the small box the molecules are whizzing around and some
molecules will leave the box through that small hole into the vast
space, so the chances of returning into the small box are near to zero.
Will there be a near vacuum in the small box after some time? If not,
why?
 ANSWER:
ANSWER:
This is, I believe, the same as the small box being permeable
to H2 but not N2; all that is different is the time it
would take to reach equilibrium. Equilibrium would be when the rate of H2
leaking out would equal the rate leaking back in. I believe the temperatures
in and out would remain the same but the pressure outside would get greater
as H2 leaked into the larger volume while the pressure in the
smaller volume would get smaller. It seems to me that equilibrium would be
reached when the number of hydrogen molecules per unit volume was the same
inside as outside. That would correspond approximately ("vastly larger")
to a pressure reduction of a factor of Vsmall box/Vlarge
box for the small box.

 QUESTION:
QUESTION:
I am confused as to how an anti-particle and a particle can
collide. If the fundamental particles only exist at points and don't
have any volume, how exactly can two particles ever actually collide
with each other?
 ANSWER:
ANSWER:
Many elementary particles are not point particles. Others may
be but the size may be a useless concept on very small scales. But whether
or not particles touch begs the question of whether they can interact with
each other. All particles have fields which extend away from the particles
and it is via these fields that particles interact with each other. This is
not solely a quantum concept; an asteroid passing by the earth is deflected
even though the two never touch. Similarly, a particle and an antiparticle
can interact and annihilate without ever "touching".
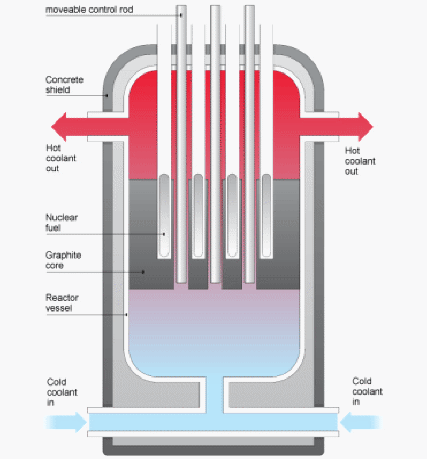
 QUESTION:
QUESTION:
One of my friends (an oncologist, so no dummy) tells me that modern nuclear power plants have a safety switch that will automatically send all the rods into a graphite core in case of emergency which will then prevent a nuclear accident, such as Chernobyl or Fukushima, and will safely contain the fissionable material for.....essentially...ever. I can't find a reference to such a safety device on the internet, although I may be just looking in the wrong place. My understanding is that all nuclear power plants will fail at some point and breach the containment container if water is not constantly supplied. Which is correct?
 ANSWER:
ANSWER:
There are many kinds of reactors with many kinds of safety
systems. What we can learn from earlier accidents is that we should never
get cocky about their safety. That doesn't mean that they are not incredibly
safe, but surely never perfect. Your friend, though, seems to have something
confused. For a nuclear reactor to work, there must be an abundance of
thermal (slow) neutrons to initiate the fission. However, each fission
releases fast neutrons and, for the geometry of the reactor core, you could
not have a self-sustained reaction without slowing them down. The purpose of
graphite in a reactor is to slow down the fast neutrons (not all reactors
use graphite as a moderator). So to send the fuel rods into graphite would
make things worse, not better. The very first reactor, at the University of
Chicago during WWII, had bars of graphite gradually added until the reactor
went critical (critical means there is one new fission for each fission).
The simplest reactor has a bunch of rods called control rods, often made of
cadmium, which absorb neutrons efficiently; these are dropped into the
reactor core in the event of an emergency to cause the reactor to go
subcritical. But accidents can cause damage which cause such safety systems
to be inoperative.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Do nuclear power plants require a constant supply of water to remain safe? I'm not talking about the expended fuel rods, but about the core itself. Without water, will a power plant go critical at some point?
 ANSWER:
ANSWER:
First, the terminology. "Going critical" is not bad, it is
necessary for energy to be produced. Here is how it goes:
-
First
with the control rods all the way in, the reactor is subcritical which
means that any time a fission happens, fewer than one more occur. Each
fission is like a lighted match which goes out without starting a fire.
-
Now, start pulling the control rods out.
Eventually you reach the point where more than one fission happens after
each fission; this is called supercritical. So the rate of fission
increases and you have to be careful to keep it from "running away".
-
When it reaches the rate you want, maybe 1020
fissions per second, you have to stop the increasing rate by putting the
control rods back just far enough so that the reactor is critical—each
fission causes another so now energy is produced at a constant power of
P=E∙1020 per second where E is the energy of a
single fission. This would be some number like P=1 gigawatt (GW).
Now, to the crux of your question. You are producing
energy, in the form of heat, of 1 GW which is one billion joules of energy
per second and that energy has to be carried away
somehow or else the whole reactor will heat up and melt (the dreaded
"meltdown"). The most common way to carry that energy away is with water and
the heated water is used to drive turbines to generate electricity. If you
do not do something to take the heat away, you have a disaster. (I just made
up 1020. Don't quote me on that, it is just to illustrate.)
 QUESTION:
QUESTION:
So if you have a negatively charged iron ball (on the end of a plastic rod) and it exerts a strong attractive force on a penny even though the penny is neutral. How is that possible?
 ANSWER:
ANSWER:
The electrons in the penny are free to move because it is a
conductor. When the negatively charged ball comes close to it the electrons
on the side closest to the ball are repelled to the other side of the penny.
The side of the penny closest to the ball is positively charged and closer
to the the ball than the side which is negatively charged, so the penny experiences a net
attractive force toward the ball.
 QUESTION:
QUESTION:
If I mounted a gun against a force gauge that measured in pounds and fired it in a vacuum and then fired it in my back yard would it read any different? How much of the recoil is actually produced by the gas pushing against the air in front of the muzzle or is it all newton thrust? There are people who claim that brakes on guns actually pull the gun forward counteracting newton force from acceleration which makes about as much sense to me as moving a boat by standing on the deck and pushing on the mast. Others who claim that part of recoil is from newton force and part is from the gas pushing against the air in front of the muzzle.
 ANSWER:
ANSWER:
This is a little tricky as are most problems which involve
air drag. First of all, look over an
earlier answer about the
recoil of an M4 carbine. To do my rough calculations, I will assume all the
data refer to a gun fired in vacuum; muzzle velocity of 940 m/s, bullet mass
m=0.004 kg, gun mass 2.77 kg, bullet diameter 45 mm. I will assume
that the acceleration along the length of the barrel (0.37 m) is uniform.
(Be sure that you realize that the muzzle velocity is the speed with
respect to the gun, not the ground.) So, the bullet starts at rest and
the equations which give its velocity and position at the end of the barrel
are 940=at and 0.37=½at2 where a is the
acceleration and t is the time to reach the end of the barrel.
Solving these two equations, I find that t=7.87x10-4 s and
a=1.2x106 m/s2. Using Newton's second law,
F=ma, we can now estimate the force experienced by the bullet during its
flight down the barrel as 0.004x1.2x106=4800 N=1079 lb. Now,
suppose that there is air in the barrel. As the bullet flies down the barrel
it will experience air drag which will be a force which will work against
the force propelling the bullet and therefore the muzzle velocity will be
smaller. As you will see from earlier
answers, a fairly good approximation for air drag force on an object
with cross sectional area A going with speed v is Fdrag≈¼Av2.
For the 45 mm bullet, A≈1.59x10-3 m2, so taking the average speed to
be 940/2=470 m/s, I find Fdrag≈88 N=19.8 lb. This will be,
I believe, an underestimate because the bullet is not just plowing through
the air as it would outside the rifle but compressing the air in front of
it. Now the net force on the bullet is about 4800-88=4712 N. Now, the
average acceleration will be about 4712/0.004=1.178x106 m/s2,
slightly smaller; the corresponding time and muzzle velocity are t'=7.93x10-4
s and 934 m/s. In the earlier
example I found the bullet speed v and recoil velocity V
to be v=938.6 m/s and V=1.4 m/s; my (very rough) estimate for
including the effects of air are v=932.7 m/s and V=1.3 m/s.
There is slightly less recoil in air. The average force on the gun during
the firing time is the same as the force on the bullet (Newton's third law) ≈4800 N=1080 lb for vacuum, ≈4712
N=1059 lb including air. That sounds like a lot, but keep in mind that it
only lasts about 0.8 milliseconds. I have included a lot of details here, but you can
understand it qualitatively: because the bullet has to accelerate through
the air which causes drag, the muzzle velocity will be smaller so the recoil
velocity will be smaller as well.
 QUESTION:
QUESTION:
Is it possible to accelerate neutrons?
 ANSWER:
ANSWER:
A scientist is usually loathe to say something is impossible.
In order to accelerate something, you must be able to exert a force on it.
Does a neutron ever feel a force? Of course it does, the nuclear force or
strong interaction is what holds neutrons inside nuclei and this is an
extremely strong force. The problem is that this force is also a very
short-range force which drops to almost zero as soon as you are a few
femptometers (1 fm=10-15 m) away from the nucleus. So, although a
neutron can be accelerated in principle, I can conceive of no way to do it
in practice. So, I will go out on a limb and say that it is impossible to
build a workable neutron accelerator.
 NOTE
ADDED:
NOTE
ADDED:
Neutrons also have a magnetic dipole moment, so they will
experience a force if you put them in a nonuniform magnetic field with an
extremly strong gradient. Again, this is not really practical for a
real-world accelerator.
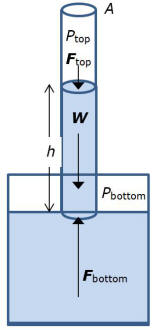
 QUESTION:
QUESTION:
The other day I was having people over for dinner .
Among them was a physicist and a chemist .
The physicist talked about a puzzle he learned in school.
It goes like this .
He said : How high can one suck up water in a vertical pipe.
The pipe can be as long as you want and the diameter does not play a role .
We did not know : he then answered : you can only suck it up ( not pump it up ) 10 meters .
He talked about creating a vacuum and the difference in pressure at top op the pipe and below .
He also used a formula something like this roo ( the greek letter r ) times g times h .
roo being the density , g 9,81 m/sec . and h being the height.
At 10 meters he came out at Zero I believe.
What is your opinion on this matter .
Is it like that and can you explain this a little better than our company .
 ANSWER:
ANSWER:
Here is the situation: A long tube of cross section
A
is stuck into a reservoir of water. The pressure at the top of the tube is
Ptop and you can adjust this pressure. The pressure at the
bottom of the tube is Pbottom and it is equal to
atmospheric pressure which is approximately 105 N/m2.
The water rises in the tube to some height h. The density of the
water is ρ=103 kg/m3, the acceleration due to gravity
is approximately g≈10 m/s2, and the volume of the water in
the tube is V=Ah, so the weight of the water is W=ρgV≈104Ah.
The force due to pressure is the pressure times the area, so there is a
force up on the bottom of Fbottom=105A
and a force down on the top of Ftop=PtopA;
there is also a force down on the column of water of its own weight W.
Since the column is in equilibrium, Fbottom-W-Ftop=0=105A-104Ah-PtopA,
so 105-104h-Ptop=0. If the
top is open to the atmosphere, Ptop=105 and so
h=0; the water will not rise in the tube at all. The best a pump
which is "sucking" can do is to make the pressure at the top zero, so, in
that case, h=105/104=10 m.
I think you should think of the column as being
pushed up by the atmospheric pressure, not "sucked" up by the vacuum.
 QUESTION:
QUESTION:
Eventually, every star in the universe will collapse and form a black hole right? what will happen when every star has finally collapsed and there is nothing but black? will the universe fill up with hawking radiation?
 ANSWER:
ANSWER:
As I state on the site, I normally do not answer
astronomy/astrophysics/cosmology questions, so you might want to get more
information elsewhere. Your statement that every star will become a black
hole, though, is wrong. Only stars with masses greater than a lower limit of
about 3-4 solar masses will become black holes. Many stars end their lives
in spectacular explosions called novae or supernovae; these events scatter
the material from the star and provide the matter necessary for future star
formations. The ultimate fate of the universe is uncertain but with the
discovery of dark energy it would seem that it is likely that it will die
with a whimper as remaining black holes evaporate and any remaining matter
just expands away.

 QUESTION:
QUESTION:
In Halo video game series there are Magnetic Accelerator Cannons on orbit around planets that can launch a 3000 ton magnetic projectile to 4% lightspeed. These cannons use the principle of the coil gun. These projectiles have a kinetic energy of 216000000000000000000 joules which translates to around 51.6 gigatons of tnt. So these cannons seem to have really unrealistic velocities for these projectiles. What would be the problems in developing these cannons to defend the human species from possible alien invaders? I know energy is one but I've heard that that if you were to accelerate a projectile to these kinds of speeds they would turn into plasma from the sheer amount of energy being transferred into them.
 ANSWER:
ANSWER:
I think you will get the picture of why this is a
preposterously impossible weapon if you read an earlier
answer. There the speed was much higher but the mass much smaller. Here
are the practical problems in a nutshell:
-
To accelerate it to this speed in a reasonable
distance the force required would be so large as to totally disintegrate
the projectile and the cannon for that matter.
-
Think about the recoil of the cannon. Unless its
mass was much bigger than 3000 tons, much of the energy expended would
be wasted, not to mention the disruption of the orbit. This would be a
good reason to have it mounted on the ground rather than orbit.
-
Where are you going to get the necessary
energy? I agree with your number for the kinetic energy of the
projectile (½mv2
works fine for this relatively low speed and a ton here is a metric
ton), ≈2.16x1020 J. Suppose it took one minute to get this
much energy; then the power required would be 2.16x1020/60≈3.6x1018
W=3.6x109 GW. This is about 1,440,000 times greater than the
current total power generated on earth of about 2500 GW. (Of course,
that does not take into account the recoil energy of the cannon itself.)
-
Oh yeah, I almost forgot. There is no evidence
whatever for alien bad guys.

 QUESTION:
QUESTION:
If I were to drop an empty wine bottle out of an airplane flying at say 35,000 feet above the ocean at 300 mph, would the bottle hit the surface of the water hard enough to break the bottle? I read somewhere something about terminal velocity being 120 mph, so would the resistance of the atmosphere slow the wine bottle to 120 mph by the time it made impact with the ocean? And would 120 mph be enough to shatter the wine bottle, or would it depend on how choppy the seas were versus a flat water surface?
 ANSWER:
ANSWER:
When I answer questions involving
air drag and terminal velocity, I
usually use the approximation that (in SI units) the force F of air
drag is F≈¼Av2 where A is the area presented
to the wind and v is the speed. So, as something falls, the faster it
goes the greater the drag force on it so that, eventually, when the drag
equals the weight, the object will be in equilibrium and fall with constant
speed. Since the weight W is mg where m is the mass and
g=9.8 m/s2, the terminal velocity can be calculated: ¼Avterminal2≈mg
or vterminal≈2√(mg/A). So the
terminal velocity depends on the mass and size of the falling object and
your 120 mph is most likely not correct. Also, how it falls determines the
terminal velocity since it has a much bigger area falling broadside than
with the top or bottom pointing down. I figure that if it falls broadside
there will be a bigger pressure on the fat side than the neck which will
cause a net torque which will make it want to turn with its neck pointing
down; so I will assume that is how it falls . I happened to have an empty
wine bottle in my recycle bin which has a mass of about 0.5 kg and a
diameter of about 8 cm. When I calculate the terminal velocity I get vterminal≈63
m/s=140 mph. The 120 mph number you heard was probably a typical terminal
velocity of a human, and it is just coincidence that the wine bottle has a
terminal velocity close to that.
It is hard to say whether it would break or not. I
think probably not. Suppose that it took 1 s to stop. Then the average
force on the bottle would be F=ma=(0.5 kg x 63 m/s)/(1 s)=31.5
N≈7 lb which the bottle should be able to withstand. I
know that they say that at high speeds hitting the water is like hitting
a brick wall, but if the stopping time were 0.1 s the force would still
only be about 70 lb.
(Who would have thought that I would find a picture
of a falling wine bottle? You can find anything on the web!)
 QUESTION:
QUESTION:
This question is regarding Newton's cradles. Let's say a particular
one had 5 balls. We pull back 3 balls and let go. Now the other side
must rebound with 3 balls as well. This means that the middle ball must
carry on swinging. Does it ever theoretically stop for the briefest of
moments? What about in real life with compression and other factors?
 ANSWER:
ANSWER:
I presume you have read the recent
answer below. Usually, in collision problems, we ask what is going on
before the collision and after the collision, but not during the collision.
The details during the collision time depend on the details of the
interactions among the balls which we generally do not know. So in cases
like Newton's cradle, we approximate the collision to occur in zero time and
therefore approximate all accelerations to be instantaneous; this is clearly
not the case since it would require an infinite force to stop or start a
ball instantaneously. So, to be more realistic, we must, as you have done by
mentioning "compression", devise some model for the collisions. With steel
balls we could assume that each was a very stiff but perfectly elastic
spring which compressed during the collision. Then, assuming the collision
were perfectly elastic (again an approximation), the collisions would happen
in a very short but nonzero time. The two incoming balls would stop in a
short time because the middle ball would exert a large backward force on
them and the two outgoing balls initially at rest would get up to speed in a
very short time because the middle ball would exert a forward force on them.
Therefore, with this simple model, assuming all the balls are identical, the
middle ball would experience a zero net force during the collision time and
so it would proceed forward never changing its speed. I could imagine that
the middle ball might slow down slightly and then speed back up to its
original speed, but not stop. Even if the collisions were perfectly
inelastic, the middle ball (and all others) would move with speed 3/5 the
speed it came in with afterwards. Whatever happens, the middle ball would
certainly never be at rest.

 QUESTION:
QUESTION:
the book i am reading says, "while walking on ice, one should take small steps to avoid slipping because small steps ensure smaller friction". Is the statement true? I think that yes, we should walk with small steps but because they ensure larger friction because of larger normal reaction. Is the book or i am right?
 ANSWER:
ANSWER:
The coefficient of static friction is larger than the
coefficient of kinetic friction. When you walk, static friction provides the
forward force to accelerate you forward. However, if you try to accelerate
forward too quickly on ice, the required friction will become too large for
static friction to be the situation and you will slip. Therefore, you want
to walk such that each step requires less friction than usual so that you do
not slip on the icier surface where the coefficient of static friction is
smaller than usual. Your book is right.
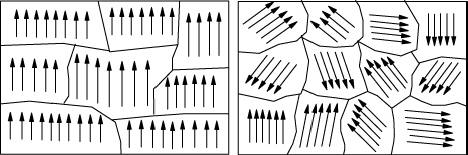
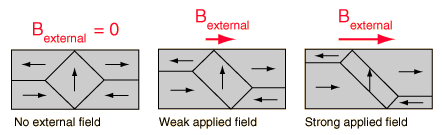
 QUESTION:
QUESTION:
What causes a magnet to have a higher Tesla than an other magnet. Is it due to how dense it is. What I mean is it determined on how much mass and or weight it has. Is it due to how many particles that whole magnet has.
 ANSWER:
ANSWER:
Permanent magnets are made from ferromagnetic materials.
These include iron, cobalt, nickel, and some rare-earth materials. Iron is
the most common and easily magnetized. The property these materials have
which allow large magnetic effects is that the unpaired electrons, which are
themselves tiny magnets, of the iron atom couple to unpaired electrons in
neighboring atoms such that the electrons' magnetic moments (essentially NS
orientations) align. There is then the possibility that the whole
macroscopic piece of iron could be a very strong magnet since there would be
something like 1023 electrons all pointing in the same direction.
This alignment only happens at temperatures below the Curie temperature (7700C
for iron); therefore if the temperature is too high, the material is not
ferromagnetic. As the iron cools down, small regions called domains form
which are magnetized by coupling of electrons, but these domains all have
randomly oriented magnetizations so that the net magnetization is about zero
as shown in the right-hand drawing in the left figure above. Now, if you put
the iron in a strong magnetic field, many domains reorient to align with the
external field as shown in the left-hand drawing in the left figure above.
It is not quite that simple; what happens is that the boundaries between
domains migrate to cause more domains to be aligned with the field as
illustrated in the simplified figure on the right above. You have now
created a permanent magnet because if you turn off the external field, the
iron will have a net magnetization. The problem is that there will be a
tendency of the domain boundaries to drift back, but not all the way when
the field is turned off; this is called hysteresis. The way to make a better
permanent magnet is to cool it in a strong magnetic field which will cause
more domains to point in the direction of the external field in the first
place. I have read that this process can be made more effective by hammering
on the iron while it cools. The strength of the magnet depends on how
successful you are in this initial magnetization. What is important as well
is the material from which the magnet is fabricated. There are many
materials, composites, alloys, ceramics which are ferromagnetic; you can
read about some of these materials on
Wikepedia.
 QUESTION:
QUESTION:
I want to know, why time is scalar quantity? Whereas it do have a direction i-e future. If time was only magnitude it could go in past as well but it only flows toward future through past. In short, Time has a direction so why it is a scalar quantity?
 ANSWER:
ANSWER:
In terms of classical physics, the future is not a direction
because direction refers to spatial coordinates; you cannot say that t=5 s
north, for example. Special relativity, though, puts time on a more equal
footing with space and we usually work with 4-dimensional vectors, 3 spatial
and one time components to a vector. One example is a displacement vector,
Rx=x, Ry=y, Rz=z,
Rt=ict,
where i=√(-1) and c is the speed of light. The form of
Rt
depends on how you define your 4-dimensional geometry, but this gives you
the idea. The length of the vector R is given by R=c2t2-x2-y2-z2.
There is still something different about time, though; I have heard many
physicists admit that "we don't really know what time is."
 QUESTION:
QUESTION:
This one has bothered me since seeing it on TV the other evening. The device called Newton's Cradle, that executive metal ball swing toy found on many desks - I understand the basic principles of the conservation of motion, energy, etc. My mind can also wrap itself around the fact that when you raise and drop one ball, one ball on the opposite side responds by moving. What I don't understand though is why when you raise and drop two balls, TWO balls on the other side respond by moving. It would seem that to conserve energy/motion, the kinetic energy of the two balls that was raised would be transferred into the last ball and it would swing out twice as much as the two balls that started the motion. How do the two balls on the end "know" that it was two balls that started it? Can you please explain this?
 ANSWER:
ANSWER:
Be clear that the approximation to use is that the collisions
are elastic, both energy and momentum must be conserved; for steel balls,
this is a pretty good approximation. OK, let's assume that two balls come in
with speed v1 and one ball goes out with speed v2.
Conserving momentum, 2mv1=mv2 or v2=2v1.
Now, look at energy: E1=½(2mv12)=mv12
and E2=½mv22=½m(2v1)2=2mv12.
Energy is not conserved, mv12≠2mv12.
You can actually prove if that a mass M comes in, only if the mass
going out is M will both energy and momentum be conserved. Here is
the proof:
-
momentum: MV=mv => v=(MV/m)
-
energy:
½MV2=½mv2=½m(MV/m)2
=> M=M2/m => m=M
-
since m=M, v=V from momentum.
Nature "knows"! You can't fool Mother Nature.
 QUESTION:
QUESTION:
Does an inertial frame of concept actually exist or is it only an ideal concept?
 ANSWER:
ANSWER:
It depends on what you mean by an inertial frame. Originally,
an inertial frame was defined to be any frame in which Newton's first law
was true; that is where the name comes from since an alternate name for
Newton's first law is the Law of Inertia. So in Newtonian physics, a frame
is not inertial if it accelerates relative to a frame that is. When special
relativity was developed by Einstein in 1905, an inertial frame was one in
which all the laws of physics were correct (the principle of special
relativity). In general relativity, only if the gravitational field is zero
do you have an inertial frame. There is no such place in the universe.
However, the whole concept of an inertial frame is much less important in
general relativity because the principle of special relativity is now
expanded to include any frame of reference.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
What if we consider only newton's laws? Is there any frame of reference in which newton's laws are strictly valid? Also, is it necessary to consider to consider any matter as frame of reference? Can't we choose just empty space as our reference frame, since, i think, it would be perfectly inertial.
 ANSWER:
ANSWER:
Newton's laws are never correct laws of physics, strictly
speaking. They are excellent approximations for speeds much less than the
speed of light. There is no such thing as "empty space", so although you can
think about such a frame as being inertial, it is still conceptual, not
real. But, if you imagined a frame very far from any large masses (almost no
gravity) which was not being accelerated (engines off), you would have an
excellent approximation to a Newtonian inertial frame.
 QUESTION:
QUESTION:
If the gravitational field is changed ,will the velocity of sound change?
 ANSWER:
ANSWER:
It is gravity which holds the atmosphere on the earth. If
gravity got stronger, for example, the air at sea level would get more
dense. Sound travels faster in a denser gas.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
i like this answer.but i have one more question related it. .If there is no air,will the velocity will change in solid object? If the answer is no,then why does the velocity of light change when gravitational field is changed?
 ANSWER:
ANSWER:
Only to the extent that the change in gravity compresses the
solid. It makes no sense to compare light and sound which are entirely
different physical phenomena. The reason gravity bends light is
general relativity and the
equivalence principle.
 QUESTION:
QUESTION:
How can one determine the velocity of two objects that fall at the same time with a difference in weight to gain the same acceleration of gravity to hit the ground at the same time?
 ANSWER:
ANSWER:
I guess you are asking why two objects of different masses
dropped simultaneously hit the ground simultaneously. You could have found
the answer on the FAQ page. You can get
the details there. The idea is that although the earth exerts a bigger force
on the bigger mass, the bigger mass has more inertia and there a force is
less effective in accelerating it. The two exactly cancel so that any mass
has the same acceleration due to gravity. This is only true if air drag is
negligible; for example a bowling ball and a feather will obviously not hit
simultaneously.
 QUESTION:
QUESTION:
I recently learned how to solve the wave equation in 1 spatial dimension and 1 temporal dimension via separation of variables. However, what I don't know is: What does your solution y(x,t) actually tell you about the wave and its properties? Does it tell you about the frequency, amplitude, period, etc... of the wave or what?
 ANSWER:
ANSWER:
The wave equation in one dimension is ∂2y(x,t)/∂x2=[∂2y(x,t)/∂t2]/v
where v is some constant. The solutions of this equation
are any function y with the restriction that x and t
in y occur only in the form x-vt. The most general solution
may therefore be written as y(x,t)=Ay1(x+vt)+By2(x-vt)
where A and B are arbitrary constants and y1
and y2 are any functions. (There is likely some
stipulation about the functions being "well-behaved" or some such if applied
to the real world.) The solution makes apparent the meaning of the constant
v—it is the speed the wave travels. Also, it can be seen
that any solution which is a function of (x-vt) is a wave traveling
in the +x direction with speed v and any solution which is a
function of (x+vt) is a wave traveling in the -x direction
with speed v. The answer to your question is therefore that the wave
equation tells you nothing about the details of the wave except its
velocity. I would say that's nice because, as you know, the possibilities
for a wave's actual shape are infinite and it would be a real pain if we
needed a different equation for each of them.
 QUESTION:
QUESTION:
I have searched for an answer to this question in vain.
A dropped large ball, with a small ball on top, will bounce and transfer the upwards momentum into the small ball, launching the small ball very high into the air. (As far as I understand this, I saw a demo).
Ignoring air resistance for now, how heavy would the large ball have to be, to launch a one kilogram weight into orbit, and what would the height of the drop have to be?
As an example, a 100 tonne ball dropped from 10 metres, with a 1kg ball on top, does a bounce, what is the velocity result for that?
How does the elasticity of the ball affect it? (eg, a large metal ball or weight might just impact the ground).
 ANSWER:
ANSWER:
This problem is fully explained and worked out at
this link. The final result, if the mass of the big ball is much bigger
than the mass of the little ball, is that the speed the little ball rebounds
is given by v≈3√(2gh) where h is the height from which it was
dropped. This means that the masses really do not matter. The height to
which the smaller ball bounces is 9 times the height from which it was
dropped. It is assumed that all collisions are perfectly elastic. The speed
required for a near earth orbit is about 8x103 m/s, so h=v2/(18g)=3.6x106
m! To put this in perspective, the radius of the earth is about 6.4x106
m, so h is about half this. This is a really rough calculation because
g
will be considerably smaller (by a factor of about 0.4) at this altitude.
Even if you did make this work, the ball goes straight up and you need it to
go horizontally to go into orbit. I think it is not a very practical idea!
 QUESTION:
QUESTION:
First, I want you to know you have the best site on the web for answering physics questions. Here's my question: The dark energy responsible for the acceleration of the expansion of the universe is about 10 to the 120th power weaker than what theories regarding dark energy say it should be. No one can explain this vast discrepancy. Has any physicist suggested that maybe the strength of dark energy is diffused throughout a multiverse of universes so we only observe a fraction of it in our universe?
 ANSWER:
ANSWER:
Thanks for the insightful comment! As I state on the site, I
normally do not answer questions on astronomy/astrophysics/cosmology, so you
should get another opinion from someone more expert; guess
AskThePhysicist.com is not the best after all. The only "theory" of dark
energy I am aware of is the famous cosmological constant in Einstein's
theory of general relativity which he added to make the universe static
(which was the current picture at the time). He later, after Hubble's
measurements, removed the cosmological constant calling it his "greatest
blunder". I believe that reinserting the cosmological constant can reproduce
the expansion data with an appropriate choice of constant. Of course, this
is really just empirical and not a theory. I truly believe that nobody has
any reasonable theory related to dark matter or dark energy and am one of
the rare people who simply say that maybe we do not understand gravity as
well as we think we do. I will be happy to change my mind if, for example, a
direct
observation of dark matter is made. Current evidence is indirect—the
rotational dynamics of galaxies and the time at which galaxies first formed
to name a couple. I have nothing to say about multiverses.


 QUESTION:
QUESTION:
Hi, I always wondered about one thing about sound, maybe you could help me out. Let's say we have a guitar and a flute. Both hit the same note, but we don't hear the same sound. Why is the sound different, even though the frequency is the same? What gives the sound its "character"?
 ANSWER:
ANSWER:
Your "character" is what musicians call timbre (pronounced
tam-brr). Your question is a good one and has been
answered before.
 QUESTION:
QUESTION:
Lightening rods used to protect the buildings, are made to be pointed . Is there any scientific reason behind that ?..... what is that if it is so?...........why these protecting rods are not made round or of some other shape ?
 ANSWER:
ANSWER:
Surprisingly (to me), this is a question not fully
understood. What is known for sure is that the primary purpose of the
lightning rod is to provide the electric current of a lightning strike with
a low-resistance path to the ground; that is its main function. The
reasoning for having a sharp point is, presumably, to help prevent a
lightning strike. A thundercloud carries a large negative charge; the
resulting strong electric field induces positive charge on the ground and
objects on the ground. But, when the lightning rod becomes charged, the
density of charge near the point becomes large and so there is a very strong
electric field around the point. This field is so strong that it can
actually ionize air molecules nearby and the resulting electrons go to the
point and ultimately to the earth and the positive ions go up to the cloud;
this is called corona discharge. So the cloud becomes less negative and the ground and
all on it becomes less positive, resulting is a weaker field and lower
chance of lightning. Well, that is the reasoning but, as I stated at the
start, actual data supporting this are sparse or nonexistent. Certainly
corona discharge happens but whether it makes a significant difference in as
huge a system as a thundercloud is not clear.
 QUESTION:
QUESTION:
Newton's first law of motion says that an object will remain at rest or travel in a straight line at a constant speed unless an outside force comes into contact with it. This means to me that a ball will not move unless a force is applied to it. If it is moving then it will move in a straight line at a constant speed unless acted upon by an outside force.
Given Newton's first law of motion, is it possible for a chemical solution to be able to move itself without an outside force being applied?
 ANSWER:
ANSWER:
No isolated system can "move itself". It can change itself,
though. Here is an example of a chemical reaction which causes "change" but
not "motion". A bomb, at rest in the middle of empty space, explodes into
100,000 little pieces plus a bunch of hot gas consisting of molecules. It no
longer looks like the bomb we started with but where the
center of mass of
the bomb was is still where the center of mass of all the debris is and ever
will be. So, what we mean by "moving" for a complex system is the motion of
the center of mass.
 QUESTION:
QUESTION:
What role does the force of friction play in the movement of a cycle....?? I have learnt that the friction acts in the forward direction on the rear wheel and backward direction on the front wheel.How can it be...?? I think I am missing a broader link to why a wheel actually rotates.
 ANSWER:
ANSWER:
In this discussion I will ignore all friction except that
which occurs due to the contact of the wheels with the road. The two kinds
of friction we normally learn about in elementary physics courses are static
and kinetic friction. Kinetic friction is the frictional force between two
surfaces which are sliding on each other; it is kinetic friction which stops
a box sliding across the floor. Static friction is the force between two
surfaces which are not sliding on each other; it is static friction which
keeps your bike from skidding when turning a corner. A third contact
friction force is called rolling friction; this is not terribly important
for a bike but is the force which will eventually stop you if you coast on
level ground and you are most aware of it if your tires are
under-inflated, harder to pedal. Rolling friction on both wheels will always
point backwards. First think about a bike which is not skidding. If you go
in a straight path on level ground without pedaling, only rolling friction
stops you and neither kinetic nor static friction are in play. Now suppose
you start pedaling to accelerate forward. Think about what your back wheel
"wants to do"; if the road were icy, the wheel would spin and the force
which keeps it from spinning on a dry road is static friction. The road will
exert a forward force on the wheel to keep it from spinning. A force is
required to accelerate anything and this static friction force is what
accelerates your bike forward. The friction on the front wheel is just the
rolling friction backwards. Finally, suppose you brake: if both brakes are
applied gently enough that you do not skid, static friction on both front
and rear wheels will point backward; if both wheels skid during braking,
kinetic friction on both front and rear wheels will point backward. You
probably know that if you apply the brakes so that they are not quite
skidding, you will stop in a shorter distance than if you skid. When you
round a curve, both wheels have a static friction force which points
perpendicular to your direction and toward the curve's center because you
are accelerating when you move in a circle even if you are going with
constant speed. More detail on
rolling friction and on
bicycle turning can be found
in earlier answers.
 QUESTION:
QUESTION:
I regularly contribute to another website that I will not mention here, but we had a discussion on a particular subject matter and one topic which came up was kinetic energy of an object moving close to the speed of light.
Specifically an assertion was made that an object traveling 85% of c would have kinetic energy equal to a matter / antimatter reaction of the same mass as the traveling object.
0.5mv^2 did not produce compatible numbers unless one assumed quite low efficiency of the M/A reaction. It was then stated to me that formula is not valid to the situation, as it fails to account for the increased mass of an object traveling at such speeds.
I'm no physics professor, but that seemed a little fishy to me. I attempted to divine an answer to this with the use of some Google-Fu, however it seems my Google-Fu is not strong enough, as I found multiple conflicting answers (and even multiple conflicting formulae to determine the kinetic energy in such a situation.)
So since my Google-Fu has failed I figured I would ask you. Do you need a different formula to calculate the kinetic energy of an object traveling at such speeds, and if so what is that formula?
 ANSWER:
ANSWER:
You have come to the right place! From your
discussion, that unnamed website is the wrong place to get physics
right. The expression ½mv2 for kinetic energy is true
(approximately) only for speeds much less than the speed of light. There is
no mystery about what kinetic energy is in special relativity, but I will
not go through the derivation. The total energy E of a particle with
rest mass m is E= E=mc2/√(1-v2/c2).
If the particle is at rest, v=0 and E=mc2. If the
particle is not at rest, it still has its mc2 energy and
everything else must be kinetic energy K: K=E-mc2.
That is all there is to it.
[It is not at all
clear what is meant by "a
matter/antimatter reaction of the same mass" in your question; I will just
briefly discuss particle/antiparticle pair creation and required kinetic
energy.]
For your case (v=0.85c):
E=mc2/√(1-0.852)=1.90mc2,
so K=0.90mc2.
There is therefore not enough kinetic energy to create another particle of
the same mass (which I am assuming the remark in your question about
"antimatter" refers to). The way to create an antiparticle, for example an
antiproton, is to collide a fast proton with a proton at rest; the energy
required to create one particle of the same mass takes quite a bit more than
mc2 of kinetic energy because momentum must also be
conserved, so the particles cannot be at rest after a collision. Also, you
cannot simply create a mass out of kinetic energy, you have to create a
particle-antiparticle pair so in the proton experiment you end up with three
protons and an antiproton. It turns out that the incident proton kinetic
energy energy needs to be 6mc2. The advantage of a
collider is that the momentum is zero so you only need to have each proton
with kinetic energy mc2 to create a proton-antiproton
pair.
Here is an added detail since I am sure that the
expression for K above looks unfamiliar to you. If v<<c,
1/√(1-v2/c2)≈1+½v2/c2+…;
this is just a binomial expansion and, if you are not familiar with
that, try it yourself: e.g. if v/c=0.05, 1/√(1-v2/c2)=1.001252
and 1+�v2/c2=1.001250. So now we can
write K≈mc2(1+½v2/c2)-mc2=½mv2.
Tada!
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Just to clarify a bit the discussion which led me to asking you arose out of one concerning hypothetical weaponry. One individual asserted that a projectile traveling 0.85c would have kinetic energy equal to a matter-antimatter bomb with a similar warhead yield. [Thus a 500kg projectile would have energy equal to the energy released by the reaction of 250kg of particles annihilating with 250kg of antiparticles] I figured being a real physicist you would not want to waste too much time drawn into a discussion on the purely hypothetical topic. Thus my question came to you, since my original calculation for kinetic energy using 0.5mv^2 with m=500kg provided significantly less energy than E=mc^2 with m being 500kg.
The website in question is TVtropes.com which analyzes elements common in fictional works literary, TV, Film, and others.
 ANSWER:
ANSWER:
Well, my answer gives you almost mc2 of
kinetic energy. The speed to get exactly mc2 is 0.866c.
But, you have no comprehension of how much energy is involved here. I think
you would be interested in an earlier answer along
these lines based on the movie Eraser.
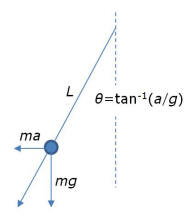
 QUESTION:
QUESTION:
I had asked you a question and you had answered it. To illustrate your point, you had quoted an example that a pendulum hanging from the ceiling of a car moving with a uniform acceleration makes an angle with the vertical. Now we have been taught in our course as well. We have also learnt that tangent of the angle is equal to a/g. My question is that will that pendulum exhibit uniform oscillations if it is displaced from its normal position?
 ANSWER:
ANSWER:
I presume that by "its normal position" you mean its new
equilibrium position off the vertical. The answer to your question is that
it will exhibit oscillations about this position; the period, though, will
not be given by T≈2π√(L/g) but rather by
T'≈2π√[L/√(g2+a2)].
This is most easily understood by introducing a fictitious force ma
opposite the direction of the acceleration. Now you can see that the force
exerting a torque on this pendulum has a magnitude of m√(g2+a2)
rather than mg as in the unaccelerated pendulum. So it is just like
the usual pendulum analysis with a somewhat larger acceleration due to
gravity.
 QUESTION:
QUESTION:
I know that visible light has much more energy than microwaves but how is it that microwaves can heat food while visible light can't? Not even gamma rays (which we wouldn't want to use for our food anyway) can heat thing like microwaves.
 ANSWER:
ANSWER:
First, it is not energy that matters, rather power, the rate
at which energy is delivered to what you are trying to heat. While it is
true that a visible-light photon has more energy than a microwave photon (E=hf),
you cannot make a statement about total energy without knowing how many
photons of each you have. So, if you concentrate light from the sun to a
spot you can burn paper. But, there must also be something going on beyond
power, something about how the radiation interacts with what you want to
heat. For example, even very intense light will not greatly heat up a sheet
of glass because almost none of the light will be absorbed, thereby giving
its energy to the glass. Microwave radiation is just the right frequency to
excite vibrations of water molecules, so many of the impinging photons
are absorbed and give their energy to the food—heating it.
 QUESTION:
QUESTION:
I have two carts of identical dimensions and one of them are more massive. They both will be released on the same ramp at the same height. They will also travel on the same track. My question is why does the less massive cart travel farther when the more massive has more energy.
 ANSWER:
ANSWER:
I am not sure what the picture is. I am assuming you mean
identical ramps followed by identical long, horizontal, tracks. It is true
that the heavier car starts with more energy, but, neglecting friction, it
reaches the bottom with the same speed as the light car for the same reason
that Galileo's Pisa Tower experiment had the light and heavy balls reach the
ground together. The question you ask has been asked many times before; on
the FAQ page you will find two links
to earlier answers and there you will find links to more. As you will see,
there is no rule that the lighter car will go farther (or go faster at the
bottom of the ramp). If there were indeed no friction, the two cars would
always have exactly the same motion. With the kind of friction we usually
think about—bearings, rolling friction, any sliding, etc.—elementary
physics tells us that the force of friction is proportional to how hard
surfaces are pressed together and that would be proportional to the weight
of the cars, so again it should be a dead heat. If air friction is taken
into account, the heavy car should win. The lesson here is that this
experiment depends strongly on the details of the design of the cars and
that friction is not a simple as is presented in elementary physics classes.
 QUESTION:
QUESTION:
My understanding is iridium is electrically conductive and basically forms a subterranean shell around the Earth, the K-T boundary. The Earth's core, consisting of rapidly rotating molten iron, constitutes a kind of dynamo. Would it be possible to use the iridium layer to gain access to the electrical energy that is produced by the Earth's core?
 ANSWER:
ANSWER:
The iridium is not like some sort of contiguous shell of
irridium, it is just a much higher concentration than normally found on
earth. Typically, the abundance of iridium in the earth's crust is on the
order of 0.3 parts per billion and the abundance in the K-T boundary (now
usually called the K-Pg boundary) is about 100 times greater; 30 parts per
billion is still too low to think of the iridium as a viable conducting
medium.
 QUESTION:
QUESTION:
why does setting a large camera flash off near a cymbal cause it to ring?
 ANSWER:
ANSWER:
See an
earlier answer.
 QUESTION:
QUESTION:
Why is it that when we feel a breeze, we feel a bit cooler? Why doesn't the friction between the air and our bodies increase our body temperature?
 ANSWER:
ANSWER:
One of the ways our bodies regulate temperature is
persperation; since it takes energy to evaporate water, heat flows from your
body, cooling you. Increasing air flow hastens this evaporation. To
demonstrate this, get a wet rag and twirl it rapidly through the air—it will
get cold. The gain due to air friction is negligible which you can prove by
holding a thermometer in the air flow—it will not heat up.
 QUESTION:
QUESTION:
This might fall into the astrophysicist category, but it might also just be basic physics. If the universe is expanding, and that expansion is like a 3D balloon surface (i.e., expanding everywhere at once), then the space occupied by each atom or particle in the universe is expanding to. But the atom is not expanding. If the atom stays at the center of each parcel of space, then the atoms in collections of atoms should be moving apart. It doesn't seem like this could be true. What is wrong with the thinking?
 ANSWER:
ANSWER:
Athough I don't usually answer astrophysics questions, I
think I can answer this one. If space is expanding, everything is expanding,
a meter stick expands and you and all your atoms expand, and there would be
no obvious way to detect it.
 QUESTION:
QUESTION:
what is the difference between l and L in atomic theory?in one book L is given as energy shell and in one book L is represented as orbital angular momentum of electron...so i want to say that energy shell can also be represented as 1,2,3 but orbital angular momentum is always rep.as L so which one is right??
 ANSWER:
ANSWER:
Notation can be confusing sometimes. In atomic physics,
capital letters starting with K are often used to denote shells containing
electrons with the same principal quantum number n: n=1 is the
K shell, n=2 is the L shell, n=3 is the M shell, etc.
The magnitude of the total orbital angular momentum of a quantum state is
almost always denoted by L. The value of L is determined by
the orbital angular momentum quantum number ℓ: L=ħ√[ℓ(ℓ+1)]
where ℓ =0,1,2,3… Also of importance is the projection (component) of
the angular momentum on to a z-axis, Lz=mL,
where m=-ℓ,-ℓ+1,-ℓ+2…0…ℓ-2,ℓ-1,ℓ.
(Note that it is usually conventional to use script ell (ℓ) rather
than l.)
 QUESTION:
QUESTION:
When testing quantum entanglement, how do experimenters know with certainty that the property (ex: spin) being compared in each entangled particle hasn't already been established before the particles left the scene (of entanglement)?
 ANSWER:
ANSWER:
This is, of course, a fundamental and important question.
Unfortunately, description of experiments to determine this is rather
complicated. The most accessible discussion for laypersons that I have seen
is in the book
The Emperor's New Mind by Roger Penrose.
 QUESTION:
QUESTION:
Are any known or theoretical substances able to react physically with neutrinos? I had a thought that if a reaction with these stubbornly weak interacting particles could be achieved that, because of the ungodly abundance of them, they could be used as some sort of power source. Specifically if a material could be found that would react to neutrinos in a similar fashion to the way photovoltaic cells react to photons.
 ANSWER:
ANSWER:
Essentially, the answer to your question is no; there is no
"material" which will interact with neutrinos. The reason is that to
interact with a material as photons do with photocells, you interact with
the atomic structure of the material and this is done via the Coulomb
(electromagnetic) force and neutrinos do not interact electromagnetically.
In fact, neutrinos do not interact via the nuclear force either. The only
way they interact is via the weak interaction. Nuclear beta decay is
mediated by the weak interaction, so you need to use a neutrino to induce an
"inverse beta decay" which is the way neutrino detectors currently in use
work. But, the probability of this happening is so tiny that you need
gigantic detectors and still get very low reaction rates. You can forget
your idea for abundant free energy from neutrinos!
 QUESTION:
QUESTION:
If an entangled pair were separated by x-distance and one of the pair is annihilated via an anti-matter to matter reaction, does the other one in the pair become annihilated?
If so then FTL information can be realized by using the explosion as a state change seen in real time at the "other side."
 ANSWER:
ANSWER:
If it were a photon, it cannot be annihilated. If it is a
charged particle, annihilation would be caused by its encountering its
antiparticle. But the other entangled particle could not disappear because
that would violate charge conservation. It would simply be put into the
appropriate state depending on the state its entangled mate was in when it
was annihilated.
 QUESTION:
QUESTION:
How does a Dyson fan, with no moving parts, work?
 ANSWER:
ANSWER:
Here is a
video of Dyson
himself explaining how it works. As you see, it does have moving parts
(a concealed "impeller").
 QUESTION:
QUESTION:
I'd like to know:
a) Can vectors somehow be associated with areas? (why or why not?)
b) Can vectors somehow be associated with mass ? ( why or why not?)
i'm asking this question because in my classroom a teacher has said that we can associate a vector with this unit: area, but we can't associate a vector with mass. At that moment he gave us a doubtfull explanation which let us confused(particularly i don't trust this "truth").
 ANSWER:
ANSWER:
a) Vectors may represent a displacement, that is, their magnitude is a length and direction is the direction of the displacement. Two vectors, tail to tail define a parallelogram. The area of the parallelogram is the dot product of the two vectors,
A∙B=ABcosθ where A and B are the magnitudes of the vectors and
θ is the angle between them. In that sense, two vectors may be
associated with an area. Also, sometimes an area may have a direction.
Consider a cube of side L. Each face has an area L2.
You could think of the area as a vector by assigning a vector which is
perpendicular to the surface, but you have to specify whether this vector
points into the cube or out of the cube. Usually, we specify the vector to
point out of the enclosed volume. This turns out to be very useful in
calculating things like flow rate through an area, flux through an area, etc.
b) A vector could never be associated with mass because mass has only
(unlike displacement or area) a magnitude associated with it, never a
direction.
 QUESTION:
QUESTION:
de broglie's wavelength is h/mv. But we know that velocity has meaning when we describe it relative to something. Velocity with respect is referred to in the formula h/mv? Is is with respect to the observer? Does that mean that wavelength of the same object can be different to different observers?
 ANSWER:
ANSWER:
That is exactly what it means�the velocity, hence the
momentum, hence the wavelength depend on the observer. But this is just the
same as in classical physics and the wavelength aspect is just the doppler
effect for particle waves.

 QUESTION:
QUESTION:
i am a university senior student. my department is elementary science education. I know that every atom that is in our planet was once created in stars. I know that first H used to create He and all the way to iron. However, iron is not the last element in periodic table how other elements are formed? Thank you for your answer.
 ANSWER:
ANSWER:
As you note, iron is the heaviest element created in stars;
the reason is that iron is the most tightly-bound nucleus and therefore any
heavier elements will require that energy be added rather than energy being
released by fusion (which is what stars do). Heavier elements are created in
very energetic events like novae and supernovae.
Recently it has been found that collisions between neutron stars also
play an important role, particularly for the element gold.
 QUESTION:
QUESTION:
When a gravitational wave pass earth the time tick a bit faster or slower.
Can the universe create a gravitational pulse, that make the time stop or go infinitely fast, when the gravitational pulse pass earth?
 ANSWER:
ANSWER:
If you increase the gravitational field, clocks run slower.
Presumably, a passing gravitational wave would have an increased
gravitational field. Your second question makes no sense, but since I know
of no way to make time stop or go infinitely fast, I guess the answer is no.
 ADDED ANSWER:
ADDED ANSWER:
Actually, since gravitational field is a vector, if the
direction were opposite the earth's field, the net field would be smaller so
clocks would run faster.
 QUESTION:
QUESTION:
So, if i have 2 cars with same speed and mass then they collide together and stop what will happen to the momentum?
 ANSWER:
ANSWER:
Momentum is a vector quantity, so if one car is going south
and the other north, their momenta are mv and -mv which means
that the total momentum is zero. Since the momentum is zero after the
collision, the momentum was conserved.
 QUESTION:
QUESTION:
why there is always a loss in total K.E of the two bodies,when they collide inelastically(i.e, when coefficient of restituition is 0)? whereas, In elastic collision, there is no loss in K.E .
if u ans that loss in K.E is used to deform the colliding bodies, than what about 2 rigid bodies (with glue) colliding inelastically with each other?
 ANSWER:
ANSWER:
Actually, collisions of macroscopic bodies are never
perfectly elastic. There is no such thing as a perfectly "rigid" body,
anything will deform some if a force is exerted on its surface, even if very
little. What you are asking is 'what are the mechanisms for energy loss in a
collision?' One loss of energy is from sound; sound waves carry energy and a
collision makes sound so that accounts for some inelasticitity. But, most
energy is lost to "frictional forces" and the final energy loss appears as
heat—the colliding objects get hotter. Think of a collision between two
rubber balls; each deforms somewhat but, since it is like a spring, it has
acquired potential energy. Then when the balls go back to their normal
shape, that potential energy is converted back into kinetic energy, and if
no energy is lost, the collision is elastic. But in the real world there is
no such thing as a perfect spring—you cannot get back all the energy you put
into compressing a real spring due to losses of work done against friction
which heats the spring up; that is called damping. A collision between two
billiard balls is very close to elastic because very little is lost to
friction when they compress. To find a truly elastic collision you need to
go to atomic or nuclear scales. One example is
Rutherford
scattering where alpha particles collide with gold nuclei and, although
some alpha particles scatter inelastically by exciting the nucleus, most
just bounce off without losing any energy.
 QUESTION:
QUESTION:
How to calculate the terminal velocity of a tomboller marble with a a diameter of 42mm, It's made of glass I think. Mass I am estimating is close to 100g.
Is the reason the change in velocity gets smaller when dropping the marble from increasing heights due to the process of air resistance and its approach to terminal velocity speed?
 ANSWER:
ANSWER:
When an object is falling, there are two forces on it, its
own weight mg down (m is mass, g≈9.8 m/s2 is
the acceleration due to gravity) and air drag Fdrag up.
The air drag gets bigger as the the object goes faster, so eventually it
will reach a speed where the air drag equals the weight. When this happens,
the net force is zero and the object moves with constant velocity as per
Newton's first law; this is called the terminal velocity. I have answered
many questions involving air drag,
and my favorite way to estimate the force is Fdrag≈¼Av2 where
A is the
cross sectional area the object presents to the air and v is the
speed; this is only correct if you use SI units, meters, kilograms, and
seconds. In your case, A=πR2, so ¼πR2v2=mg
or v=(2/R)√(mg/π). Putting in your numbers,
v=53 m/s=119
mph=191 km/hr.
 QUESTION:
QUESTION:
We just
bought a telescopic hedge trimmer... The Weight of the trimmer is
3.8kg...this is then attached to a pole which extends between 1.85m and
2.8m. The handle to switch on the trimmer is at the base of the pole. I
have just been using it for the past 2 1/2 - 3 hours and now my arms and
shoulders are aching....What is the weight of the hedge trimmer at full
extension and angled at say 45 degrees from the floor? because it feels
a lot heavier than 3.8kg! Doesn't gravity have something to do with it?
 ANSWER:
ANSWER:
What you are encountering is torque. You do not just need to
hold up the weight, you need to keep it from rotating, so you are certainly
going to need to exert more than 3.8 kg of force. (A kg is not really a unit
of force, but it works for this context.) What the forces are which you must
apply will depend on how you hold it. To make things simple, I will choose a
particular way way you might hold it—by pushing on the end of the pole with
a force F2 which makes an angle φ relative to the
horizontal and pulling with a force F1 perpendicular to
the pole at some distance s from the end—and solve the problem in
general; then I will apply it to your situation to illustrate how the forces
necessary are much bigger. I will assume that all the weight W is at
the other end of the pole, that the pole is of length L, and that the
pole makes an angle θ with the horizontal. I don't think you want all
the details of my calculation, so I will just give you the final results if
you say that the whole thing is in equilibrium so all the forces and torques
must add to zero.
So, for your case, L=2.8 m, W=3.8 kg, θ=450,
and I will estimate s to be about 0.3 m.
As you can see, each arm has to exert a force more
than 6 times the weight! Of course, all the weight is not at the end as I have
approximated; the center of gravity will be somewhere closer to you and so
the effective value of L will be smaller which will make the forces
smaller. So, suppose W acts at 1 m instead of 2.8 m. The results are
then:
-
φ=-21.80
-
F1=8.96 kg
-
F2=6.82 kg.
This would be a a force about 2 times the weight on
each arm.
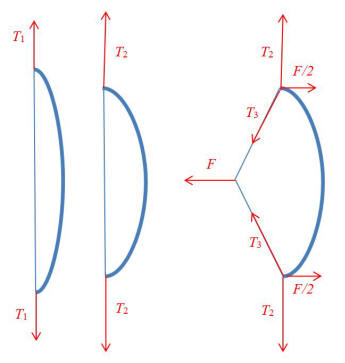
 QUESTION:
QUESTION:
This is a question that relates indirectly to my profession.
I am a chiropractor , a colleague of mine has found a way to initiate a muscle relaxation response by treating individual muscle attachments a certain way.
He explains his theory by using the example of a bowstring. He says that when one pulls the string on a bowstring to shoot an arrow the tension of the string attachments onto the bow diminishes cause the two ends are approached.
Somehow I have my doubts about that.
I know the direction of tension changes, but does the tension decrease ?
Is there a way this can be measured and whats your opinion on this matter.
 ANSWER:
ANSWER:
First, look at the bow not drawn, shown to the left. There is
a tension in the string, T1. The bow pulls up on the
string at the top with a force T1 and down on the string
at the bottom with a force T1. (It is a common student
mistake to say that if the bow pulls up at the top with force T1
and down on the bottom with T1, the tension in the string
is 2T1. This is wrong.) I think we can agree that if the
string is shortened, as in the middle picture, the tension will
increase and so the force the bow will exert top and bottom, vertically will
increase. So, a flexed bow will exert a greater force vertically on the
string, T2 at both ends. Now, if the bow drawn by pulling
on the original string with a force F such that the bow is the same
shape as in the middle picture, each end of the string will also have a
horizontal force F/2 as shown in the right figure and the vertical
components (T2) will remain the same. In the drawing, T2
and F/2 are the forces the bow end exert on the string, and
T3 is the force which the string exerts on the bow end; Newton's third law says
these must be equal and opposite, so the string
has a tension T3=√[(F/2)2+T22].
Clearly T3>T2>T
1,
so you are right, the tension increases when you draw the bow.
Finally, anybody who has ever drawn a bow knows that the farther you draw it
the harder it gets to draw it farther; in this sense, the bow is like a
spring where to pull it a little requires little force, but to pull it a lot
requires larger force.

 QUESTION:
QUESTION:
So i'm building a big aquarium for a friend who is a performing mermaid. The tank is going to be built on a trailer for easy transport. the framing will be steel. My question is what formula do i need to determine what thickness acrylic i'll need to make the tank strong but as light as possible. If i'm building a 6 ft. by 4ft by 4ft tank.
A: Hw do you determine p.s.i. for water in a container by volume. (pressure exerted on the walls)
B: what formula do i use to plug in gallons, p.s.i., etc..
C: what can i use to determine the min. thickness of acrylic i'll need.
 ANSWER:
ANSWER:
The gauge pressure P (pressure above atmospheric) at a
depth D in a fluid with weight density ρ is P=Dρ.
The density of water is ρ=0.0361 lb/in3, so the
P=0
PSI at the top of the tank, P=(0.0361 lb/in3)x(48 in)=
1.73 PSI at the bottom, and P=(0.0361 lb/in3)xD in
general (D in inches). Since atmospheric pressure is about 14.7 PSI,
the pressure in a tank of this depth is relatively small. So, the answer to
your question A is that the pressure does not depend on the volume at all,
only on the depth; you could have a tank 4 ft deep and a mile on the sides
and the pressure would be just the same as yours. You could also calculate
the total force on a side of width W; that force is ½WD2ρ,
but that number is not very necessary for you since the force is uniformly
distributed across W. For example, the force on each 4x4 side would
be about 2000 lb and on each 4x6 side would be about 3000 lb. There is also
a torque on each side about the top edge of each side of WD3ρ/3
(which tries to rip the side away with the top edge as the pivot). Those
torques are about 32,000 in∙lb=2660 ft∙lb and 48,000 in∙lb=3990 ft∙lb for
the short and long sides. Your questions B and C are engineering questions,
not physics, but there is certainly no formula in which you would plug in
either a volume or a pressure to get a thickness of the plastic because, as
I showed above, only the depth matters. You can probably check with an
aquarium supply place how thick your plastic needs to be for a depth of 4
ft. I found
one
site which recommends 3/4 in thick for a 30 in depth; the purpose of
this is to prevent bowing of the acrylic which would be mainly a horizontal
bulge, not to hold back the water from breaking the plastic. Some bulging
may be acceptable to you to save costs. Looking at the numbers above,
though, I think an important concern for you is the strength of the
framing—those edges have to hold a lot of force and torque. You might also
think about the force on the bottom of the tank which will be about 6000 lb.


 QUESTION:
QUESTION:
From what I understand, the vast majority of the large bodies in the solar system rotate and orbit in a counterclockwise fashion relative to their magnetic north pole. Is this true for most/all solar systems in this galaxy/the observable universe, or is it different every time? Why is this?
 ANSWER:
ANSWER:
First, you have a misunderstanding. Most rotations in our
solar system are counterclockwise as viewed from the North Star
(Polaris). The magnetic pole of any particular body has nothing to do with
this rule. In fact, the earth's NS poles have swapped positions many times
in the distant past. Also, many of the bodies in the solar system (like our
moon) have no or negligible magnetic field. So, to state the rule you need
to specify whether you are viewing the solar system from "above" (which I
will call looking down on our north pole) or "below" (which I will call
looking down on the south pole); in the latter case, the rule would say all
rotations are clockwise. The reason is that in the current best theory for
formation of the solar system says that a huge cloud of gas and dust
collapsed to form it. That cloud will have an angular momentum (net
rotation) which remains and speeds up as the cloud collapses. To see more
detail, see an earlier answer. Any other
planetary system in the galaxy will have a similar rule with most objects
spinning the same direction, but not likely in the same direction as ours.
Other galaxies do not have the same rotation as our Milky Way galaxy because
when we see them, some are seen edge on and others are seen face on. (Both
of those pictured are spiral galaxies which spin like a big plate.)
 QUESTION:
QUESTION:
What determines how far light can travel? For example, if light
travels 186,000 m/s why can't I see a flashlight shining a mile away?
I'm sure it has something to do with the amount of energy emitted from
the beam or something like that, but can you give me a scientific but
lay answer?
 ANSWER:
ANSWER:
Light can travel forever until something interacts with it.
The light moving through the air is continually interacting with air
molecules, scattering out of your line of sight, getting absorbed by atoms,
etc. The more atoms between you and the source, the more of the light
will be removed from the original beam. Eventually, enough light will be
absorbed or scattered that your eye will not be able to detect the surviving
intensity. I think, though, that a flashlight would be visible from a mile
away on a reasonably clear (no fog) day. Think about light we see from
stars; from many stars it has been traveling for millions of years.
 QUESTION:
QUESTION:
Why do helicopters spin with the earth even when they are hovering?
 ANSWER:
ANSWER:
Because the helicopter flies relative to the air and the air
spins with the earth.
 QUESTION:
QUESTION:
when we go up in the atmosphere we feel the pressure, when we go down in the water we feel the pressure then why don't we feel the pressure on ground level
 ANSWER:
ANSWER:
Most life has evolved in an environment where the pressure is
about 1 atmosphere, about 105 N/m2. Only if the
pressure is significantly lower (going up into the atmosphere) or higher
(going down in the water) do we notice the difference.
 QUESTION:
QUESTION:
According to law of gravitation by Isaac Newton gravitational force is directly proportional to the product of masses of 2 bodies..so if we consider light as stream of photons ,they have negligible mass so light should not get bent in black holes but still it happens why?
 ANSWER:
ANSWER:
Because Newtonian gravity is wrong. See my FAQ page for
questions about general relativity, the more correct theory of gravity.
 QUESTION:
QUESTION:
if you are travelling on a train at 0.99c and look outside into a mirror (not connected to the train) would you see yourself as being thinner?
 ANSWER:
ANSWER:
No. Although the mirror is at rest relative to the ground,
your image is moving with the same speed you are and would therefore be at
rest relative to you. If you are interested in how you would appear if you
were moving past someone on the ground, see an
earlier answer. Interestingly, even though you would actually be thinner
(length contraction), you would not look thinner!
 QUESTION:
QUESTION:
what is the electromagnetic constant?
 ANSWER:
ANSWER:
Actually, I have never heard of something called the
"electromagnetic constant". The two fundamental constants of
electromagnetism are the permittivity of free space, ε0=8.854x10-12 m-3∙kg-1∙s4∙A2
and the permeability of free space, μ0=1.257x10-6 m∙kg∙s-2∙A-2.
Interestingly, the speed of light c is given by c=1/√(μ0ε0).
Maybe the speed of light c is the answer you are looking for.
A second possibility is the coupling constant for
the electromagnetic field, usually called the fine-structure constant.
This is α=e2/(4πε0ħc)=1/137.036.
Note that this constant is dimensionless.
 QUESTION:
QUESTION:
why do turning eggs lift their bottom (=heavier end)?
 ANSWER:
ANSWER:
The reason is pretty complicated, but the qualitative idea is
that friction does work which converts kinetic energy (spinning) into
potential energy to lift the center of mass of the egg. You can read about
it an link to more detailed explanations at
this
link.
 QUESTION:
QUESTION:
According to the parallelogram law of vector addition , the resultant of two vectors represented in both magnitude and direction by two adjacent sides of a parallelogram starting from a point, their resultant is given in magnitude and direction by the diagonal of the parallelogram starting from that point.
Also , components of a vector are the influences of that vector in a given direction.
My question is, infinite numbers of parallelogram( or even regular polygon) can be constructed to get a vector as the desired resultant. Does this mean that a given vector has infinite number of pairs of components? Does a vector have influences in all these directions simultaneously? Also, why is it only the rectangular components that we widely consider in physics problems?
 ANSWER:
ANSWER:
Your last question is important because, although you could
call any two vectors which sum to a third vector the components of the
vector, we do not. Only vectors perpendicular to each other and adding to a
third are called components. The reason for this is simple―you only have to
do trigonometry of right triangles to work in this scheme. But the answer to
your first question is that, yes, indeed there are an infinite number of
different ways you could resolve the components of a vector because there
are an infinte number of coordinate systems you could choose. Any coordinate
system rotated through any angle would give different but equally correct
components as any other coordinate system. This is equivalent to saying you
may choose any coordinate system you like to solve a problem.
 QUESTION:
QUESTION:
If the speed at which a satellite is falling towards the earth is increasing steadily at 10m/sec/sec why does the orbital speed not have to increase to keep pace with this and prevent the satellite meeting the ground?
 ANSWER:
ANSWER:
You have to remember that acceleration is a vector. The speed
necessary for orbiting is horizontal (think of a circular orbit), the speed
acquired by the satellite due to falling is vertical. So, although the
satellite is gaining velocity, the horizontal velocity is not increasing.
Your question could apply to asking why, if I throw a ball horizontally with
some speed, the ball does not go into orbit.
 QUESTION:
QUESTION:
I don't understand the reason why, when charged electrons are accelerated toward an equally charged positive plate with a hole through the center of the plate as in a simple two electrode cathode ray tube, why do the electrons keep moving past the positive plate? I would think that the electrons that pass through the hole should again be attracted to the positive plate and should slow down and reverse direction. What am I not understanding?
 ANSWER:
ANSWER:
The high voltage is applied across the cathode and the anode
so that there is a very strong electric field between them. But, beyond the
anode, the field is very weak. Think of a parallel plate capacitor where the
electric field outside the plates is zero.

 QUESTION:
QUESTION:
I was wondering, since in quantum phisics observing a phenomenon can change the odds of this phenomenon to arise, how can a detector in a particle accelerator can be trusted? shouldn't it already vary the result simply by measuring them?
 ANSWER:
ANSWER:
A single measurement causes the probability for that
particular particle to be 100% of what you measure. If, however, you
make many measurements then you can deduce the distribution of
probabilities. One measurement never gets you any useful information in
quantum mechanics. For example, suppose you want to measure the mass of a π0
meson. This particle decays into two photons, so, if you measure the enegies
of the two photons and add them, this is the rest-mass energy (E=mc2)
of the meson from which you can easily deduce the mass (m=E/c2).
The graph to the right shows the results of many such measurements. Don't
worry about the units. The fact is that you might make one measurement which
gives you the mass and find that you get that m=0.026 units. You have
found that the meson you measured had that mass, but if you keep measuring
you will find that others have different masses; you have not caused all
mesons to have a mass of 0.026 units just because you determined one to have
that mass. You would be inclined to call the mass of the meson to be
approximately 0.020 units (the most probable value) with a distribution
determined by the rest of your data; the spread of these data, incidentally,
would tell you about how long this particle lives, on average, before
decaying into two photons. (Oh, by the way, any given meson has the whole
distribution of masses before you measure it; measuring it "puts it" at the
mass you measure. In other words, a particle does not have a definite mass
but a probability distribution of possible masses. Only if the particle is
stable (like an electron) does it have a definite mass.)

 QUESTION:
QUESTION:
i am currently working on a book that deals a lot with space. while it is technically fiction, it's not heavily science fiction (no aliens or new planets or anything of the like) and i want it to be as accurate as possible. my question is, is it possible for a satellite/spacecraft to be able to have and elliptical orbit around the earth and moon, with the two bodies being the elliptical centers. the main problem i see with this idea is that the moon, well, moves, which could wreak havoc on the orbit, but i'm still wondering if it is still theoretically possible.
 ANSWER:
ANSWER:
If, by "elliptical centers" you mean foci, the answer is
absolutely no. The three-body problem has no general analytical solution. In your special
case, one approximate solution would be that if the satellite/spacecraft
were at all times very far away compared to the earth-moon distance, the
orbit would be approximately an ellipse with the center of mass of the earth
moon system at one focus of the ellipse. Another interesting case is if the
moon-earth system is approximated to have circular orbits (about their
center of mass) and the satellite/spacecraft moves in the same plane. In
that case the satellite will have a closed orbit (called a
horseshoe orbit)
or even be stationary points (called
LaGrange points)
as seen from the (rotating) earth-moon system. The picture to the right
shows some possible orbits around the sun-earth system, but would be similar
for the earth- (replacing the sun) -moon (replacing the earth) system; also
shown are the LaGrange points (L1-L5). The picture to the left shows the
asteroid belt (white dots) along with other asteroids (green dots) which
orbit with Jupiter near the L5 and L4 LaGrange points and still other
asteroids (orange points) which are referred to as Hildas; for a more
detailed discussion of the Hildas which have elliptical orbits, see the
article by
John Baez. An animation of the Trojans, Greeks, and Hildas is shown
below; keep in mind that this is in the frame of Jupiter and the sun which
is approximately stationary but the picture from outside would have Jupiter
going around the sun counterclockwise. I
think these are the most interesting solutions for your situation, but
there are numerous other special analytical situations of the three-body
problem which you can research starting with the
Wikepedia article.
 QUESTION:
QUESTION:
If 100 kg person was standing on an imaginary platform in space
(feet toward the sun) the same distance as the earth and not in orbit
around the sun, how much would they weigh?
 ANSWER:
ANSWER:
The force F on a mass m by a mass M
where the two are separated by a distance R is given by Newton's
universal law of gravitation, F=MmG/R2 where G=6.67x10-11
Nm2/kg2. Putting in m=102 kg, M=2x1030
kg, and R=1.5x1011 m, I find F=0.59 N=0.133 lb.
This would mean that near the equator the "weight" of a 100 kg man would be
roughly 980.59 N at midnight and 979.41 N at noon (not taking into account
the moon which would probably have a larger contribution than the sun).
 QUESTION:
QUESTION:
What if everyone in the world jumped at the same time?
 ANSWER:
ANSWER:
The short answer is nothing or nothing you could measure. A
longer answer is that if all six billion people were at one location and all
jumped up with a speed of about 1 m/s, the earth would recoil with a speed
V=m/M where m is the mass of all the people (about 3x1011
kg based on an average mass of about 50 kg) and M=6x1024
kg is the mass of the earth. So, V=5x10-14 m/s; the earth
would recoil by much less than the size of an atom in a second. It might
cause an earthquake if they were all in the vicinity of a fault.
 QUESTION:
QUESTION:
Are the equations of motion v = u + at, S = ut + 0.5at^2 , and v^2 = u^2 + 2aS applicable if a particle travels at a speed close to that of light? I think that they are applicable, and only F =ma is not, but my friend says that those 3 equations are also not. Who is right?
 ANSWER:
ANSWER:
Your friend is right. These are the classical equations for
uniform acceleration, and uniform acceleration is not possible in the theory
of special relativity for a constant force. Constant force, where F=dp/dt,
(which, incidentally, is the way Newton originally wrote his second law) can
be constant but does not result in constant acceleration. I have treated
this problem in detail in an
earlier answer; there I find that
v=(Ft/(m))/√[1+(Ft/(mc))2]
and
S=(mc2/F)(√[1+(Ft/(mc))2]-1)
(for your
u=0,
that is, the particle at rest at
t=0)
for constant force.
 QUESTION:
QUESTION:
We know that sand particles are, for the most part, composed of silica. What substance composes fundamental particles?
 ANSWER:
ANSWER:
There are many answers. Some fundamental particles (for
example, electrons or photons) are, themselves, as small as you can go.
Other particles called hadrons are composed of quarks. See an
earlier answer on composition of
elementary particles. This is as much as we know right now; maybe someday we
might find that things we think of as the smallest are composed of something
smaller yet.
 QUESTION:
QUESTION:
I have heard in a lecture that charge is conserved locally ......
what does he mean by the word " locally" here ...
 ANSWER:
ANSWER:
Charge is conserved in an isolated system which means
a system for which there are no sources or sinks of electric charge; no
electric charge can leak in or out of the "local" system. Hence, if any
positive electric charge appears, an equal amount of negative electric
charge must also appear.
 QUESTION:
QUESTION:
Im sitting here watching the science channel, which I love! And they are talking about the core of Jupiter, which is by popular discussion they believe it is mostly metallic hydrogen. Now my question is, "if you had a 1 inch cube of metallic hydrogen, and took away the extreme pressure, would it stay metallic or dissolve into back into a gas?
 ANSWER:
ANSWER:
Metalic hydrogen is atomic hydrogen (not H2,
molecular hydrogen) which behaves like a conductor and which occurs at high
pressures. The phase diagram to the left shows that metallic hydrogen cannot
occur at pressures less than about 100 GPa≈1000 atmospheres or temperatures
above about 2000 K. Lower temperatures, say around 300 K (near room
temperature), require pressures more like 350 GPa≈3500 atmospheres. To the
right is a phase diagram for H2 at much lower temperatures and
pressures and you can see that
hydrogen will be a gas of H2 for normal conditions. Note that
atmospheric pressure is about 1 on the pressure scale and the temperatures
are far below room temperature So, the
answer to your question is that putting 1 in3 of metallic
hydrogen in an environment of normal pressure and temperature would cause it
to change to a gas of H2 molecules (hugely expanded in volume).
 NOTE
ADDED:
NOTE
ADDED:
I found this "Jupiter cake". Cake depicting the layers of Jupiter! The center (mudcake) is the theoretical rock/ice core, then comes the (almond butter) layer of liquid metallic hydrogen, and finally the (colored vanilla) liquid molecular hydrogen.

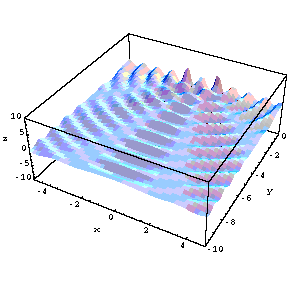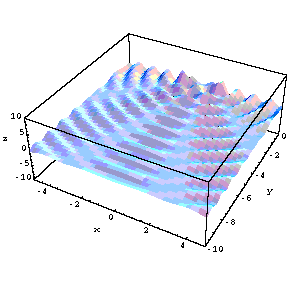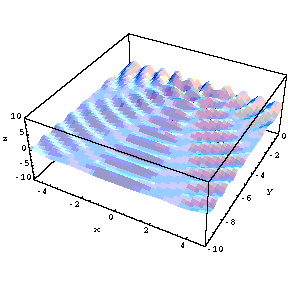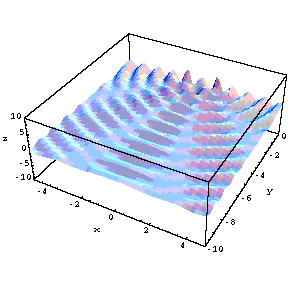
 QUESTION:
QUESTION:
Is the superposition of multiple waves simply a way of thinking about multiple waves (i.e. there is no new wave, only the original ones which can be dealt with/thought of as if they were a single wave), or is a single (new) wave created by these multiple waves? And if the latter is the case (i.e. it is a new wave), then is this new wave superimposed upon the originals (i.e. the original waves remain, but another one--their superposition--is added above them), or would the original waves combine (e.g. two waves would become one, and the original two would no longer remain)?
 ANSWER:
ANSWER:
The question you ask is all semantics. The superposition
principle simply states that, at any point in space and at any time, the net
wave displacement is the sum of all displacements of all waves. It makes no
difference whether you want to call that displacement one wave or many. The
superposition principle is the result of the fact that the wave equation is
a linear equation and therefore if A(x,y,z,t) and
B(x,y,z,t) are separately solutions to some wave equation,
then A+B is also a solution.
 QUESTION:
QUESTION:
Sir we know that there is no electric field in a conductor but still when we connect the wire to a battery current flows through it due to the prescence of electric field in it.How so?
 ANSWER:
ANSWER:
There is no (static) electric field inside an ideal conductor.
A wire is not a perfect (ideal) conductor.

 QUESTION:
QUESTION:
I read that the polarization of light is the direction of oscillation of its electric field. I also know that the magnitude of an electric field is given by the formula KQ/r^2 where K is Coloumb's constant, Q is the charge of the particle emitting the electric field and r is the distance from the particle. The fact that this formula has Q in it indicates that a particle needs a charge in order to have an electric field. Photons have no charge. Therefore, how does light have an electric field?
 ANSWER:
ANSWER:
Your statement "the
magnitude of an electric field is given by the formula KQ/r2"
is true only for the electric field of a single, stationary point
charge. However, electric fields in electromagnetic waves are certainly
generated by electric charges. But, for there to be a wave generated, rather
than just a static electric field, the charges must be accelerating. The
simplest example is the oscillating electric dipole, two equal and opposite
charges connected by a tiny spring so that they oscillate sinesoidally. The
animation to the right shows the resulting radiation from an oscillating
dipole (charges are oscillating vertically, the oscillator is too tiny to
see in this picture). The lines radiating out are loci of constant electric
field magnitude. The electric filed is perpendicular to the screen and the
magnetic field is perpendicular to the electric field and in the plane of
the screen. In nature, light usually comes from atoms which, if you think
about it, are composed of positive and negative charges and can therefore
look like a dipole when vibrating.
 QUESTION:
QUESTION:
What happens to all of the light photons that enter your eyes each day?
 ANSWER:
ANSWER:
They are absorbed by molecules in your eye and give their
energy to performing the necessary chemistry on the molecules which absorb
them to send electrical impulses to your brain for processing into images.
 QUESTION:
QUESTION:
I was just wondering about the speed of light and maybe a limiting factor?! My question is this, why can light travel faster in a vacuum, without a medium, i.e. what is it about a medium that really limits the speed of light? Gravity?!
 ANSWER:
ANSWER:
Light is an electromagnetic phenomenon. You can think of it
as containing oscillating electric and magnetic fields. When light enters a
medium, it sees the electrons on all the atoms and interacts with them. Lots
of things can happen as a result of this interaction, but the interactions
take time and so the light slows down. Gravity is not relevant to your
question.
 QUESTION:
QUESTION:
when a train is having a very large acceleration, a ball (when viewed from inside train) appears to move backwards(due to inertia).So, why doesnot a ball kept on earth moves(observed from earth), since earth is accelerating, sun is also , galaxy is also, and perhaps universe as a whole is also accelerating????
1.If u argue that the frame of reference (i.e earth) is itself accelerating, so there is no net acceleration between earth and the ball ,then this logic doesn't fit for the first case (i.e the train-ball case).
 ANSWER:
ANSWER:
The simple reason is that the accelerations of the surface of
the earth are so small that, for many purposes, they can be neglected. In
general, Newton's laws are not correct in accelerated frames of reference
unless you add "fictitious forces". If you search
this site for the word "fictitious" you will find many examples of
accelerated frames of reference. You might start with this
earlier answer.
 QUESTION:
QUESTION:
My question is Einstein explanation of space time being curved is the reason that things attract does not make sense. There is no space between an object and our planet but there is still an attraction. If space being curved is the reason why would this happen.
 ANSWER:
ANSWER:
Emptiness is still space, there does not have to be any
"stuff" for there to be space. Think of space as anywhere where you can do
geometry. For example, most of the solar system is a vacuum but you can
still talk about the volume of the solar system. Even the language which
physicists and astronomers use acknowledges this, as in "most of the universe is empty
space."
 QUESTION:
QUESTION:
When we hold a rubber ball and exert a force on it with a pin, and the pin pierces into the rubber and we say that due to large pressure because of the small surface area of the pin tip, the pin is able to penetrate into the ball. but if we keep a ball on a surface which offerers very less friction and apply the same force with a pin on the rubber ball, the ball starts to roll in the direction of the force. If we use a stick instead of a pin in the latter case, the outcome is same, and there is no meaning of pressure with which the force is applied. So is it true that the pressure has meaning only if the body on which the force is applied does not move?
 ANSWER:
ANSWER:
The average pressure is always the applied force divided by
the area over which it is applied. If you are holding the ball, you can
exert a large force on the pin without the ball moving and so there is a
large pressure where the pin touches the ball. For the ball free to roll,
the ball starts rolling when you have exerted the tiniest of forces. If you
rapidly drive the pin on the ball it will penetrate before the ball gets a
chance to get rolling. To say that pressure has no meaning, though, is
wrong; it is always force per unit area.
 QUESTION:
QUESTION:
You can stand on an empty soda can and it will support your weight. But touch a pencil point gently to the side, and the can will crumple. I'm trying to find out why.
 ANSWER:
ANSWER:
Imagine the can to be made up of many thin sticks, as
pictured to the left; I will suppose there are 100 sticks and your weight is
100 lb. Each stick must therefore hold up 1 lb. If the stick is perfectly
straight, it is able to support 1 lb but if it gets the slightest "kink" in
it, it will not and will quickly fold. But that stick is actually attached
to the sticks on either side of it, so if it folds it will drag its
neighbors with it and they will drag their neighbors and the whole can will
fail.
 QUESTION:
QUESTION:
Not, a physicist or even a student, simply a curious nurse. I was reading the papers explaining EPR and wanted to know if i was begining to understand this of if I am still way off.
When the question concerns "incompatible quantities" and that they should both have real values (but dont)... does this mean that the two arent relatable(mathmatically) or am i totally wrong?
 ANSWER:
ANSWER:
In quantum mechanics, any observable (like position,
momentum, energy, time, etc.) is associated with a mathematical
operator; an example would the position x of a particle on the x-axis
and I will call that operator X. To relate the operator with the
observable, we need to know the wave function of the particle, call it ψ(x).
Then if it happens that Xψ(x)=xnψ(x),
then ψ(x) is called an eigenfunction and xn
is called the eigenvalue which is what the position is if ψ(x)
is the wave function; ψ(x) is denoted ψn(x)
to distinguish it from other possible wave functions. If when you operate X on
ψ(x) and do not get an eigenvalue equation, then the
particle simply does not have a well-defined position. In that case, the
best you can do is predict an average value you would find if you made many
measurements on a particle with wave function ψ(x); this is
called the expectation value of x and I will not go into the detail
of how you do that. Now suppose that there is some other observable for the
same particle which we are interested in; an example would be the x-component
of the linear momentum px where the operator would be
called Px and the corresponding eigenvalue equation would
be Pxψ(x)=pxnψ(x).
Finally, we come to the answer to your question: the operators X and
Px are said to be incompatible if XPx-PxX
≠0.
In fact, for the example I have chosen, X and
Px are incompatible:
XPx-PxX=iħ. This has a
well-known profound result, namely that the position and momentum of a
particle cannot be simultaneously known to arbitrary precision, AKA the
Heisenberg uncertainty principle.
 QUESTION:
QUESTION:
Regarding special relativity's "length contraction": Is it the images of physical objects that contract via differences in relativistic frames of reference or does it claim that physical objects actually contract in length (in the direction of the 'observer's' travel?) If the latter, what is the physics explanation of "shrinking physical objects?"
 ANSWER:
ANSWER:
Physics defines length to be the difference in the positions
of two points which have been measured at the same time. With that
definition, a moving meter stick is really shorter if it moves relative to
the observer, that is a meter stick is only one meter long in its own rest
frame. The "explanation" is simply that if you apply the theory of special
relativity, this is what you find for this definition of length. I hope you
appreciate that this is a reasonable definition of length; for example, if a
car were moving by you and you measured the position of the rear bumper at
noon and the position of the front bumper an hour later, you would not call
the distance between those two measurements the length of the car. To link
to previous discussions regarding "how objects look" compared to "how
objects are", see my FAQ page.
 QUESTION:
QUESTION:
how much kinetic energy does a beam of hydrogen atoms moving at 5% the speed of light have.
 ANSWER:
ANSWER:
Well, you do not give me any information on the intensity or
length of the beam, so I cannot give you a number. I can show you how to
calculate the kinetic energy K of one hydrogen atom of mass M and you
can figure out how many atoms are in your beam. K=Mc2(1/[√(1-0.052)]-1)=0.00125235Mc2=1.88228x10-10 J where
c is the speed of light. Since the speed is quite small
compared to the speed of light, you could get a good approximation using the
classical value of K, K=½Mv2=1.87875x10-10
J.
 QUESTION:
QUESTION:
I am a professional brewer (producing beer) with a creative mind. This question combines two passions of mine mixed with an odd thought brought to mind. In the brewing process one of the final steps before pitching yeast cultures is to create a whirlpool effect with the liquid causing the solids in solution to collect towards the middle and into a cone at the bottom of the tank using centrifugal force.
 ANSWER:
ANSWER:
See an
earlier answer (posed by a professional baker).
 QUESTION:
QUESTION:
If an object (say a ball bearing) is flying through space (vacuum
and no overall gravitational field) and it heads towards a doughnut,
through it's centre and out the other side, how would the acceleration
and speed change over time?
 ANSWER:
ANSWER:
The details would depend on the masses and sizes of the
doughtnut and ball, but qualitatively it would go as follows. When the two
are far apart compared to their sizes, the gravitational force would be very
small and the ball would move with approximately constant velocity. As they
got closer, the force would increase and the ball would speed up. Since the
force would be zero when the ball was centered in the hole, there would come
a time during the approach when the force would maximize and start
decreasing; during this time the ball would continue accelerating but at a
decreasing rate. On the other side the ball would begin slowing down since
the force is now opposite the velocity; the magnitude of this acceleration
would increase until the point of maximum force, then decrease beyond that,
the ball eventually moving with the same velocity it had far away on the
other side.
 QUESTION:
QUESTION:
It is my understanding that according to Einstein, magnetism doesn't actually exist, it is just a consequence of the relative motion of electric charges and the special theory of relativity. I have read explanations of how wires with electric currents flowing in them attract or repel each other due to nothing more than the moving electrons and their interaction with each other and the atoms of the wire via special relativity. But what about electromagnetic waves, where there is a varying electric and magnetic field? Can you provide a similar explanation that invokes special relativity and electric charges to explain electromagnetic waves?
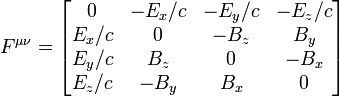
 ANSWER:
ANSWER:
I would say that it is incorrect to say that "magnetism doesn't actually
exist." This gets a little complicated mathematically, but there is actually
only one field called the electromagnetic field. It is a tensor field, not a
simple vector field and when the Lorenz transformation acts on it, the
electric field and magnetic field (which are like "pieces" of the whole
field) both change. The simplest example is if you are at rest relative to
an electric charge there is only an electric field, but an observer moving
relative to you will see both a magnetic field and an electric field
(slightly different from yours). Just for the fun of it, I have written a
form of the tensor at the right. Notice that both electric and magnetic
fields are there, they "actually exist". You might want to look at the
Wikepedia article on the
electromagnetic field tensor.
 QUESTION:
QUESTION:
I really don't understand why there are assumptions made in physics....if those assumptions are neglected then practical physics doesn't come into play??....while we study the change in acceleration due to gravity with height we consider earth to be a homogeneous sphere but while studying the variation of g with shape we consider earth to be elliptical which is the actual shape...which means that the first case is wrong if the assumption is neglected?
 ANSWER:
ANSWER:
Almost any problem in physics (or any science, for that
matter) requires making judicious approximations. Physics is straightforward
only for the simplest of cases and to solve any real-world problem usually
you decide what factors contribute in a minor enough way that their effects
may be neglected. You mention gravity, so let's use a projectile launched
from earth. What must we take into account if we want to do the problem
exactly?
-
The earth is not a perfect sphere, as you note,
so you must measure the distribution of the mass of the earth relative
to its center of mass and then find the acceleration of gravity at each
point both on the surface and above it.
-
The earth is not an inertial frame, it is
rotating, so you must take into account the (fictitious) centrifugal and
Coriolis forces. Similarly, the earth goes around the sun in an
eliptical path, so the fictitious forces associated with that
acceleration must be taken into account.
-
The moon exerts a gravitational force which we
should include; after all, the effects of this force are evident from
observing tides. The sun also exerts a gravitational force, as does
every other object in the universe.
-
The projectile is flying through the air, so we
must take air friction into account which, to complicate matters,
depends on the velocity of the projectile. Also, if there happens to be
a wind, this will exert a force on the projectile.
If we were interested, for example, in the flight of
a baseball after it was hit, we would be foolish to take all the things
listed above into account. You would never learn how physics works unless
you can see for that problem that nonuniformity of the earth, nonsphericity
of the earth, the moon, the sun, and the earth's rotation would make almost
no noticable difference if you just ignored them altogether. The only thing
you might want to worry about is air friction; after all, you could never
have a curve ball without air friction. But, even air friction is usually
neglected in most introductory physics problems because it just makes
understanding projectile motion too difficult if you are just starting to
learn physics. If you are interested, however, in calculating precisely the
orbit of a satellite (a different kind of projectile) you would certainly
need to know the gravitational field more precisely than you need to know it
for a baseball.

 QUESTION:
QUESTION:
I'm doing book research on the Triangle Shirtwaist Factory
fire, a huge fire in the early part of the last century in which many
women jumped or either fell out of a factory window from 100 feet up. I
encountered one statistic that said they hit the ground with a force of
around 11,400 pounds. This seems like way too much force to me, given
that they probably only weight 125 lbs or so. I've tried looking up easy
formulas to verify this online, but I haven't come up with anything
definitive. It seems like the variables which I can plug into an
equation are weight (I'm assuming an average of 55 kg); height (100
feet) and gravity (9.8 meters/sec squared) The site
http://hyperphysics.phy-astr.gsu.edu/hbase/flobi.html provides
boxes to plug in numbers, and they also ask for "distance traveled after
impact". This is one variable I don't know. The women (none of whom
survived the jump impact) were landing on concrete, which is of course
pretty immobile. I typed in ".01 meters" for distance traveled after
impact. ??? The site gives me a number of 1,794,870 newtons. Is it
possible to convert this into kilograms?
 ANSWER:
ANSWER:
The reason you are having problems is that it is impossible
to calculate the force just by knowing how high they jumped from, in other
words, how fast they were going when they hit. The calculation you did is one
way to estimate the force, by knowing how far the victim moved before
stopping. Of course, this is not really possible to get exactly because it
would depend on how the person hit the ground. For example, hitting head or
feet first, a reasonable estimate of a stopping distance would be half the
body height (about 1 m); or hitting spread eagle, probably more like 10
cm=0.1 m. Putting these into the hyperphysics calculator, the numbers are
about 16,000 N (corresponding to about 1600 kg or 3600 lb) and 160,000 N
(corresponding to about 16,000 kg or 36,000 lb), respectively. These are of
the same order of magnitude as the 11,400 lb estimate your other reference came up
with. In your case, you have to think about more than how much the ground
deforms, but also how the body will deform. These forces are rough estimates
of the average force.
The way I usually look at this kind of problem is
to try to estimate the force from the time of collision. From 30 m
(roughly 100 ft) the speed at the ground would be about 24 m/s. The time
to travel about 1 m to stop (again, about half body height) would be
about 1/12 s. Then, instead of using kinetic energy to calculate the
force as the hyperphysics calculator did, use Newton's second law which
says that F=mv/t=(55 kg)x(24 m/s)/(1/12 s)≈16,000 N where
F is the average force during impact. This is the same answer as
above, which it should be since it is the same physics. If there had
been a big airbag at the bottom which would increase the collision time
to 1/2 s, the force would have been more like 270 N≈61 lb, probably
nobody would have died.
 QUESTION:
QUESTION:
I understand where time comes from to an extent. Days-revolution of
the earth, year- orbit around the sun, seconds- duration of
9,192,631,770 cycles of microwave light absorbed or emitted by the
hyperfine transition of caesium-133 atoms in their ground state
undisturbed by external fields. I understand that we might not be able
to travel at the speed of light. But the hadron collider moves particles
at 99.999994% (something like that) the speed of light. If they were to
use a caesium-133 molecule would the the time of decay change or would
that be an external field being in the collider?
 ANSWER:
ANSWER:
Nobody understands what time is. However, we can
operationally define what one unit of time is. You have given a couple of
examples of operational definitions of units of time. Since Einstein came up
with the theory of special relativity, we now underatand that how fast time
proceeds depends on who measures it. The atomic clock you refer to is not
really a good example since it is the frequency of the radiation, not the
decay time. But, if you did happen to have a 133Cs clock going at
0.99999994c, it would keep time fine in its own rest frame but you
would measure it to run slow by a factor of 1/√(1-0.999999942)=2887.
In other words, when the atomic clock ticked off 1 s, your clock would read
2887 s=48 min.
 QUESTION:
QUESTION:
im having trouble understanding the concept of linear momentum in a spinning system. For example; in a system that consists of 2 masses (m and M), each on one end of an ideal bar which pivots around O, on a horizontal surface without friction and spinning with a constant angular velocity.
So I understand that angular momentum is conserved because the only forces acting on the particles are central forces (Torque=0). Is the linear momentum conserved though? using cartesian coordinates the velocity is changing direction but not absolute value. But using polar coordinates the velocity is constantly tangential. More over since the masses are not equal the internal forces that act upon the pivot point O do not cancel each other out, then I reason that for the pivot point to be at rest there is an external force which acts on the pivot point, and if there are external forces then P does not remain constant.
More over, if L= r x P
L(angular momentum)=constant
r= Constant
Then, can we say that P (linear momentum) has to be constant? or am I miss-understanding the workings of the vector product/cross product?
 ANSWER:
ANSWER:
Any particle which has an external force on it will not have
constant linear momentum. In your example, each mass has a force on it (the
stick) and so its linear momentum is not constant. This is evident since the
velocity of each mass is continually changing direction. You could also ask
about the linear momentum of the whole system. If M is a distance R from O and
m is a distance r from O and if we denote the
angular velocity of the system as ω, then the speed of M is
V=Rω and the speed of m is v=rω. So, the
magnitude
of the linear momentum is P=|MR-mr|ω. The direction of
the linear momentum vector is always perpendicular to the bar, but since the
bar is always rotating, the vector P is always changing
direction so linear momentum is not conserved. The force which causes the
linear momentum to change is the force the nail (or whatever holds the bar
to point O) exerts on the bar. There is one special case for which linear
momentum will remain constant, if P=0 which will happen if R=(m/M)r.
This is called the center of mass of the system and it is the point around
which the system would rotate on your frictionless table if there were no
nail at all. If you were in empty space and threw this "dumbbell" with an
angular velocity, it would fly off spinning but if you watched the center of
mass it would move in a straight line with constant velocity. To answer your
last question, L=rxp is a vector equation and is
true only for a single point mass. In your example, the angular momentum of
m is constant even though both r and p
are constantly changing; the reason is that the magnitudes r and
p=mrω are constant and always perpendicular to each other so that
L=mr2ωsin900=mr2ω.
Similarly, L=MR2ω for M.
 QUESTION:
QUESTION:
Will the force between two charges decrease if we place an infinite conducting plate between them?
 ANSWER:
ANSWER:
It depends on what the charges are. Qualitatively what
happens is that the electric field lines from both charges no longer
penetrate the sheet, so neither charge feels any force from the other
any more. However each charge now induces a charge on the surface nearest to
it and the net effect is like looking at a charge of the same magnitude and
opposite sign the same distance behind the sheet. So a charge of magnitude
Q and a distance d from the sheet will feel an attractive
force toward the sheet of magnitude kQ2/(4d2).
 QUESTION:
QUESTION:
Pressure is inversely proportional to volume . Volume is directly
proportional to pressure (temperature?)
then pressure should be inversely proportional to temperature but it's
actually direct . HOW ?
 ANSWER:
ANSWER:
I think you must have meant volume is proportional to
temperature (see above). So, your first statement is
V~1/P and your second (corrected) statement is V~T and so, from normal
mathematics rules, V~T/P. or P~T/V. I do
not see any problem. (I am defining the notation that ~ means "proportional
to" since my keyboard does not have the usual proportionality symbol.)
 QUESTION:
QUESTION:
An apple falls from a tree. An insect in the apple finds that the
earth is falling towards it with an acceleration g. Who exerts the force
needed to accelerate the earth with this acceleration g?
 ANSWER:
ANSWER:
I will give you two answers. First, the earth is not
accelerating with acceleration g, it just looks that way to the bug.
Second is that Newton's laws are not correct in an accelerated frame of
reference. The second answer is important if you want to understand why the
bug can't do the same calculation he could do if he were at rest and the
earth really were accelerating toward him.
A frequent example
used to illustrate the second answer is the pendulum hanging from the inside
of the roof of an accelerating car. The pendulum will not hang vertically
down but at an angle and appear to be in equilibrium as viewed from inside
the accelerating car. But, if it is in equilibrium, Newton's first law says
all the forces on it are zero but they clearly are not; only the forces of
its weight down and the tension in the string act on the pendulum and they
cannot add to zero. Newton's first law is false in the car.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
In that case these laws must not be valid even on earth, because earth is also accelerating all the time due to its motion around the sun
 ANSWER:
ANSWER:
That is certainly true. Even more important is the
acceleration due to earth's rotation on its axis. Noticeable effects are the
fictitious centrifugal and
Coriolis forces. However, these accelerations are small and Newton's
laws are excellent approximations in many circumstances. You may be
interested in a couple of earlier answers,
1 &
2.
 QUESTION:
QUESTION:
I am hoping you can help me come up with an answer to a question.
Some of my friends suffer from the delusion that I know a lot about
physics. (When in the end, I have only a very basic grasp of some of the
basic laws, enough to know how little I actually know.) One of them
asked me a question the other day, and I could not give a positive
answer. So I figured I would ask someone who actually does know a lot
about physics. I am going to rephrase the question a bit however to be
as clear as possible. The question regards how important hardness is to
a collision. Say I have two balls, which I will call A and B. Ball A is
a baseball. I throw this baseball at 44 meters per second targeting an
iron sheet 1 meter square and 10mm thick. Common sense tells me that the
baseball will bounce right off of the steel which will be largely
unaffected. Ball B is identical in dimensions, and mass to Ball A.
However the material Ball-B is made of is (picking an arbitrary number)
1000x harder than the iron plate. Will Ball-B being thrown at the same
speed do any meaningful harm to the iron plate? My first instinct was to
say no, because even being much harder than the baseball or the iron, it
is traveling the same speed with the same mass, Ball-B simply does not
have the kinetic energy required to do the work necessary to deform the
iron. But then I got to thinking about what little I know of how
hardness affects impacts (which is limited, and I am prone to
overthinking things to begin with). So, was my initial inclination
correct, or would Ball-B actually have a meaningful effect on the steel
plate?
 ANSWER:
ANSWER:
Quantifying "hardness" is tricky, but I think we can simply
say, for your purposes, that hardness is a measure of how hard it is to
deform something. Your baseball would be deformed in a vise much more than
your hard ball for the same applied force. To get at the heart of what you
are asking, I will assume that both collisions are perfectly elastic and
that the mass of the steel is enough greater than that of the balls that it
can be assumed not to recoil in the collision. So, what we will see in each
case is the ball rebounding with the same speed with which it came in.
During the collision, the steel and the ball exert forces on each other,
equal and opposite as per Newton's third law. The average force F on
the ball during the collision is equal to the change in momentum divided by
the elapsed time. The balls have equal masses m and speeds v,
so the change change of momentum for each is 2mv. So, F=2mv/t
where t is the time the collision lasted. Of course, the harder ball
will have a much shorter collision time and therefore experience a much
larger force. Thus, the hard ball exerts a much larger force on the steel.
It is force you should think about, not energy, if you want to find out if
the steel is damaged. I
do not want to get into the question of whether or not there would be
noticeable damage to the steel since that depends more on details and
assumptions. Suffice it to say that the hard ball exerts a larger force
because its collision lasts a shorter time and is thus more likely to do
damage.
 QUESTION:
QUESTION:
I read that wave packets can be written as sums of monochromatic waves. Similarly, I know that Fourier series is a means of writing any periodic function as an infinite sum of sine and cosine waves. The definition of "monochromatic" that I got on the internet said that a monochromatic wave was a wave with a single frequency. Sine and cosine waves have single frequencies. Does this mean that the phases of wave packets such as photons can be written as a mere Fourier series?
P.S. I'm in 11th grade.
 ANSWER:
ANSWER:
You are very close to understanding. Suppose you have a
periodic function (repeats every T seconds forever) with frequency f=1/T but it is not a sine or cosine but some different shape.
You can represent it with an infinite sum of sine and cosine functions of
appropriate amplitudes and frequencies f, 2f, 3f…μ This
series is called a Fourier series as you have said. However, if the wave in
question is not periodic, this will not work but something similar will. For
example, consider a packet which is a simple sine wave but which contains
only five wavelengths and is zero elsewhere; this is not periodic because it
is zero after five periods (and before the five wavelengths pass you). You
can still use a superposition of sine and cosine waves but now you need more
than just integer multiples of the frequency, you need all frequencies. (E.g.,
you also need 1.2f, 2.9f, 2.97f and all the infinite
other xf contributions.) If you have had any calculus and are
familiar with integrals, you must now do a "continuous sum" over
all
frequencies, an integration. This is called a Fourier transform.
 QUESTION:
QUESTION:
What causes matter to rotate/spin/orbit? All I can find is the
statement that in space particles of dust/gas/matter contract into a
spinning disk due to gravity (to form stars, solar systems, galaxies
etc.), with no explanation as to why the spin. I see a lot about the
conservation of angular momentum, but these discussions all presume that
the 'spin' already exists. What caused the spin in the first place?
Shouldn't gravity simply attract particles of dust, gas or matter
together along a straight path till they collide, as a magnet does to a
paper clip? The magnet does not make the paper clip revolve around it,
and if I fall off of a building, I don't spin around the earth. I fall
in a straight path till I collide with the earth. What am I missing?
 ANSWER:
ANSWER:
A star and its planets form from a cloud of dust and gas
which is hugely bigger than the size of the final star-planet system.
Imagine that this cloud is a million times bigger than the final system.
Each dust particle and molecule is moving with a random velocity; labeling
each member of the cloud by the number i, the angular momentum ℓi
of each particle of mass mi and speed vi
is miviθri=ℓi
where ri is the distance to the center of mass of
the cloud and viθ is the component of the velocity which
is perpendicular to the vector ri. Notice that if
at large distances out into the cloud all the viθ do not
add up to zero exactly, even if the sum is a very tiny number (the cloud is
almost not rotating) the angular momentum can be appreciable because
ri is very large. Probably the whole cloud has an
imperceptibly small spin but it still can have a large angular momentum. Now
the cloud starts collapsing because of its gravity. There is a very
important law in physics called conservation of angular momentum: the
total angular momentum of any isolated system must remain constant.
Here, isolated means that there is nothing which exerts torques on the
system and since this cloud is far from other large objects, it is
essentially isolated. As the cloud collapses, ri for each
particle gets smaller and so viθ for each particle
must get bigger by the same factor to conserve momentum. So, if the cloud
shrinks by a factor of a million, it will end up with a million times
greater spin. Also, see an earlier
answer.
 QUESTION:
QUESTION:
the speed of light is constant,yet we know gravity pulls on light,wouldn't light aimed directly towards a high source of gravity,such as a black hole move faster ?
 ANSWER:
ANSWER:
As light falls into a black hole, it gains energy, but not by
speeding up. The frequency increases as it falls meaning the energy of each
photon increases, but the speed stays just the same.
 QUESTION:
QUESTION:
-
With increase in velocity during free fall is there increase in simple kinetic energy without gain in mass or there is increase in relativistic KE as per velocity?
-
If object becomes more massive due to gain in velocity and relativistic KE and velocity approaches c then would there be increase in gravitational attraction exponentially as mass increases exponentially?
-
What happens to total energy if the object hits the ground and KE is dissipated.
 ANSWER:
ANSWER:
This is three questions (I numbered them), not one as required by the site
groundrules. In future, please abide by the rules.
-
The "free fall problem" has been
earlier solved. There the problem is one of constant force F=mg
where m is the rest mass. There it was shown that
β=v/c=(Ft/(mc))/√[1+(Ft/(mc))2].
Since E=mc2/√[1-β2] and
K=E-mc2,
it may be shown that K=mc2[√[1+(gt/c)2]-1].
For very large times, this becomes K≈mgct, kinetic energy
increasing linearly with time while velocity approaches a constant (c).
Hence, the answer to your first question is the energy increases where
the velocity changes hardly at all; I have often said that
"accelerators" should really be called "energizers" because once the
particle gets near c, it no longer accelerates.{Note that it is problematical what is meant by free fall. Since
relativistically you cannot have constant acceleration forever, you have
to define what you mean. I define it to be constant rate of change of
relativistic momentum as discussed in the
earlier
example.}
-
In general relativity, the gravitational field
is more generally determined by the energy density of the source, not
just its mass, so the gravitational field of the moving object increases
as its speed increases.
-
Total energy remains the same, but now goes into
sound, heat, tearing stuff apart, etc. See an
earlier answer to get some idea of how much
energy a relativistic object has.
 QUESTION:
QUESTION:
The definition of e.m.f in my book is given as, 'The e.m.f of a cell
is defined as the energy spent per unit charge in taking a positive
charge around the complete circuit of the cell'. The definition of
terminal voltage is given as 'the terminal voltage of a cell is defined
as the work done per unit charge in carrying a positive charge around
the circuit connected across the terminals of the cell'. Can you please
explain the difference between the two? How is the work done different
in these cases?
 ANSWER:
ANSWER:
The EMF characterizes the potential difference between the
terminals of a source of power when no current is flowing through the
device. It is, for example, the voltage measured across the terminals of a
battery with an ideal (infinite resistance) voltmeter. The terminal voltage
is the voltage measured by an ideal voltmeter across the terminals of a
battery if it is connected to a circuit through which current is flowing.
These can be different if the battery is not ideal, that is, if it has some
internal resistance.
 QUESTION:
QUESTION:
I am currently writing a science fiction novel and have been researching the effects of vacuum on the human body. According to the sources I looked up, a person will not explode or freeze to death if exposed directly to space. What I am curious to know is if being exposed to too much gravity would have the effect of making someone explode. If not, can you tell me what physical forces, even artificially, could exert enough internal pressure to make someone explode. This research is for use within my novel. It would help me to maintain scientific accuracy if you could give me, at least, a theoretical explanation for what could create the scenario I describe.
 ANSWER:
ANSWER:
Well, increased gravity will not cause a body to explode
either. Imagine that your weight suddenly increased by a factor of 1000.
Your puny legs would be incapable of holding you up. All your muscles would
have the same problem. You would be crushed to the ground. If the gravity
became strong enough, it would be like you were in a hydraulic press,
liquified. I do not know of anything, short of a bomb inside, that would
cause a body to explode.
 QUESTION:
QUESTION:
Light behaves like a particle and a wave(in that it collides with
matter and it has no real mass). Right? SO, why does light travel from
objects straight into our eyes (and everywhere else) why doesn't it
collide with ALL of the other light in between said object and our eyes
and then when the light reaches our eyes it would not have traveled
directly from the object but from a multitude of angles, thus distorting
the image of the object(plausibly too much to even see anything).
 ANSWER:
ANSWER:
Light does not always travel straight from an object to your
eyes. The reason you see a blue sky and not a black sky is because some
light from the sun strikes a molecule or a dust particle in the atmosphere,
scatters from that point to your eye. Sometimes light from some source finds
two paths to your eye and the light from those two paths can interfere with
each other either being brighter or darker than you would expect; this is
called diffraction but usually we do not see this because the wavelength of
light is so short. When you are looking at a leaf outside, you are really
looking at light which originally came from the sun.
 QUESTION:
QUESTION:
If you are doubling the distance what happens to the time and velocity.
 ANSWER:
ANSWER:
This question makes no sense because time and velocity are not coupled. If you double the distance you travel, the product
vt doubles and there are an infinite number of ways that can happen:
-
speed twice as fast, time the same;
-
speed the same, time twice as long;
-
speed ten times as fast, time 1/5 as long;
-
speed half as fast, time four times as long;
-
etc., etc., etc.
 QUESTION:
QUESTION:
I am a teacher in New Zealand, and am much more familiar with Chemistry than with Physics. I have been trying recently to understand magnetism better, in general, and as applied to Earth and Space Sciences. When a permanent magnet is created, what is actually lining up to create the magnetic field? I have heard it described as atoms, or pockets of charge, or micromagnets, but what does this chemically look like? Are they polar molecules within the solid? My understanding of bonding of metals doesn't include any polarity, they are positive nuclei in a 'sea of electrons', so how could a metal be aligned by charge? Is it an alteration of electron orbitals? Am I over-thinking this?
 ANSWER:
ANSWER:
An electron is, itself, like a tiny bar magnet, called an
electric dipole moment. In most materials, the electrons point in random
directions resulting in no bulk magnetism. In a ferromagnetic material like
iron, there is a quantum mechanical effect which causes the electrons
responsible for bonding to neighbors in the crystal to align their dipole
moments. An ordinary piece of iron is normally not a magnet because the
aligning of electron magnets happens only below a certain temperature called
the Curie temperature and when the iron cools down the alignment occurs
in local small volumes, each of which is pointing in a random direction;
these are called domains and are hugely bigger than atoms but still
microscopic. To magnetize the iron, you put it in a strong magnetic field
and the domains already aligned with the field will grow at the expense of
those not aligned with the field. You can also cool iron in a strong
magnetic field and then most domains will form being aligned with the
external field.
 CONTINUED
QUESTION:
CONTINUED
QUESTION:
Also, how does the movement of charged particles in the Earth's liquid outer core, or in the Sun's convective zone, actually produce a magnetic field? I have read about this effect many times, but I just can't picture chemically what this would look like. Is it that the general movemnet of ions within a fluid tends to align in the same direction over time, thus influencing other ions to do the same, and this spreading the force?
 ANSWER:
ANSWER:
(In future, please follow site
groundrules and submit single
questions!) Any electric current causes a magnetic field. So a simple
model of the earth's field would be to imagine a huge ring of current inside
the earth. The magnetic field of a current ring is shown to the left.
Compare this to the field of the earth shown to the right. Clearly a model
where the core is thought of as a collection of current loops gives rise to
a reasonable description of the earth's field. You are barking up the wrong tree
by trying to understand it chemically. I should also note that the details
of the earth's field mechanism are not fully understood.
 QUESTION:
QUESTION:
We know there are EM waves. All other waves need a medium to propagate. How does the EM wave propagate? There must be an ether.
 ANSWER:
ANSWER:
Here is what we know for certain: the speed of light in a
vacuum is independent of the velocity of the source or the velocity of the
observer. There is therefore not a medium with respect to which it moves. It
is no puzzle how light propogates, Maxwell's equations clearly predict
electromagnetic waves which have a speed c in vacuum. If you want to
believe in the æther, be my guest. But it is sort of like religion, you need
faith and will not get proof. It is not needed in electromagnetic theory,
and if it is not needed, why add it? Did you ever hear of Occum's razor?
 QUESTION:
QUESTION:
So if black holes have so much mass that light can't even escape and gravity has almost an infiniate range of influance, when our universe is at its end and black wholes have swallowed up everything will the black holes start to move toward each other and then come together? If so would this singularity be so heavy that it would rip space time and then "big bang" again?
 ANSWER:
ANSWER:
Again, I emphasize that I usually do not answer
astronomy/astrophysics/cosmology questions. I believe, though, that the
current best model of the universe has, because of dark energy, the most
likely fate of the universe not recollapsing (big crunch) but ever expanding
and black holes eventually all evaporating via
Hawking radiation.
 QUESTION:
QUESTION:
Here is the setup:
You have a larger container with 2L of water in it, and above that you have a smaller container with an airtight piston/plunger inside it. A counterweight attached to the piston. The upper (smaller) container is attached to the lower (larger) container via a pipe.
The question:
How much would the counterweight need to weigh, to pull the piston up and fill the smaller container with water?
Assumptions:
- The piston weighs nothing and has no friction.
- 1L of water weighs 1kg
My best guess would be that the counterweight needs to weigh 1kg? Is this correct?
(If not, what would it be, and why?)
(It seems simple enough, but there might be something I don't know about, that I'm not factoring in?)
 ANSWER:
ANSWER:
Why have I waited so long to answer this question? Something
about the picture bothered me and I could not put my finger on it. I kept
coming back to the picture and kept being bothered. I think I now understand
the problem. The pipe between the two containers plays a crucial role. If
the pipe is the same size as the upper container, you get one answer, the
one you want―1 kg is the unknown mass. But suppose that the pipe is very
tiny; in that case only a tiny mass would be needed because the bottom of
the upper container would hold up most of the weight of the water. Let me do
the case where there is no pipe, you just have a hollow tube of cross
section A into which the piston if fitted and which is immersed in
the water. When you have lifted the piston until half the water (1 kg) is in
the tube above the surface of the water in the reservoir and a height h
above the surface, the forces on the water plus the piston are: the weight
of the water down, W=-ρghA=-1000ghA=-g; the force of the
atmospheric pressure Pa=105 N/m2 up
on the bottom of the column,
Fbottom=PaA;
the force of the atmospheric pressure down on the top of the piston,
Ftop=-PaA;
and the tension in the string, necessarily equal to the unknown weight Mg.
Therefore PaA-PaA+Mg-g=0 or M=1 kg. Keep in mind that there is an important constraint
on the geometry of the tube: if the tube is so narrow that h>10.2 m,
no weight will be able to lift it higher and the piston will separate from
the water and there will be a vacuum between the piston and the upper
surface of the water. You can see this because if the pressure at the top is
zero, ρghA=PaA,
h=Pa/ρg=105/(9.8x103)=10.2
m; this is just a water barometer.
 QUESTION:
QUESTION:
A question about capactance, electrostatic. If a Van De Graaf or Wimshurst were connected to the ungrounded side of a parallel plate capacitor--the other side is grounded, would the capacitance be nearly unlimited, like an electrophorus? Else how could a plate with such little surface area hold such a high voltage?
 ANSWER:
ANSWER:
The capacitance of a capacitor is determined only by its
geometry and the properties of any dielectric material which may be in or
around it. Too high a voltage will simply cause it to break down.
 QUESTION:
QUESTION:
Is there a factor in Newtonian Gravity similar to the factor for precession as in GR(ie., the factor in the Schwarzschild equation for planet precession)?
 ANSWER:
ANSWER:
If you are wondering whether an orbit precession is possible
in Newtonian gravity, the answer is yes. For example, if the sun were not
perfectly spherical (which it is not), orbit precession is possible.
 QUESTION:
QUESTION:
Just read Ender's Game, and it got me thinking of relativistic travel. What would be the optimum speed (relative to Earth) that you could send a probe (say, 1 light-year), and return to Earth? Go too slow, and it takes a long time. Faster is better, but if you go too fast, then relativity starts to work against you.
 ANSWER:
ANSWER:
I am puzzled by your statement that "relativity
starts to work against you." And, what are the criteria which determine the
"optimal speed"? If you are on earth and want to get the probe back to earth
as quickly as possible, the faster the better. If you are on the probe and
want to get there and back as quickly as possible, the faster the better.
How does relativity work against you?
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
So, say there is an object 1 light-year away from the Earth. I want to send a robotic probe there, spend 1 day gathering a sample, and then return it to the Earth. If I send it at 50% c, (if I did my math correct) I calculate it would take (from my point of view on Earth) ~ 4.6 years (plus one day) to get the sample back (with only 4 years + 1 day elapsing relative to the probe). But, if I set the probe speed to .999 c, it would take me ~ 44.8 years ( + 1 day ) to get my sample, which is almost 10 times longer than .5c. This is what I mean by relativity working against you.
 ANSWER:
ANSWER:
Well, I do not know what you did, but your answers are
certainly wrong. As I understand it, you stay on earth. So, using your clock
you see a probe going 0.5c to take two years to go one light year and
2 years to get back: 4 yr + 1 day. If the speed is 0.999c, the time
out (and back) is 1/0.999=1.001: 2.002 yr + 1 day. From your point of view,
relativity is irrelevant if all you are interested in is measured by your
clocks and your meter sticks.
You might ask how much
time elapses for a clock attached to the probe. (See my discussion of the
twin paradox.) Each probe will
see the distance you see (1 ly) Lorentz contracted, the slower by √(1-0.52)=0.866
and the speedier by √(1-0.9992)=0.045 and so the elapsed times
will be 1.73 yr + 1 day and 0.09 yr + 1 day.
 QUESTION:
QUESTION:
I have been debating this for years and have read many online forums. My question regards solar heat and how it is conducted into water.
I have a large swimming pool. My current solar cover is silvery with round bubbles underside. The silvery material supposed holds heat better and warms up the water better, as well as preventing evaporation, dirt in the pool etc... I now need to replace the cover which has worked reasonably well for 6 years, but I always thought it doesn't help heat the pool much.
My thought is that diamond shaped air bubbles on the underside will have a greater surface area for transmitting heat into the water. But I cannot get a good answer on what color the material should be. These covers come in silvery, clear, dark blue and light blue. I thought dark blue would absorb more heat, but others say clear helps magnify the sun's rays and produce more heat. Still others say light blue is best, others say the silver. The benefits of these covers are multiple. They definitely do keep heat in overnight, stop evaporation, and keep pools cleaner. But I really want a cover that will help heat up the pool during the day if no one is swimming yet. So what is best? Diamond bubbles or circular? Clear or dark blue, or silver as I currently have?
 ANSWER:
ANSWER:
My knee-jerk reaction is to agree with you that the best
choice would be a dark color. However, there are many variables and you
could get tricked. To get heat into the water is the main concern for you,
not necessarily how much heat gets absorbed in the cover itself. A little
search resulted in
some
data which, if accurate, I think tells the story. Evidently, the most
important thing which determines heat transmitted to the water (heating
power) is how thick the cover is. This makes sense since the thicker the
cover, the more absorbed energy it can hold and therefore the more energy is
avaiable for heating the pool. So choose any color you like best, anything
else would be fine tuning at best. I suspect bubble shape is pretty
irrelevant too.
 QUESTION:
QUESTION:
Time dilation. 3 observers: earth, spaceship A, and spaceship B.
Both ships are rushing by the earth at .9 of c, and experience a 2:1
ratio of time passage as predicted by relativity. If spaceship A
observes clocks on spaceship B is time dilation double that as from
earth? A simple yes or no would work, but a link describing this would
be appreciated.
 ANSWER:
ANSWER:
Relativity does not predict a 2:1 ratio of clock rates of A
and B relative to earth. The gamma factor for γ=1/√(1-β2)=2.29,
where β=v/c, not 2; elapsed time on A or B as measured by
earth is earth time divided by 2.29. To find the velocity of B realtive to A
you need the
relativistic velocity addition formula
βBA=(βB+βA)/(1+βAβB)=1.8/1.81=0.9945
and so γBA=9.53 and the time dilation
relative to that seen on earth is 9.53/2.29=4.16, not double. The answer to
your question is a simple no. I guess I am your link since I gave you the
description.
 QUESTION:
QUESTION:
If I listen to two radio stations in a travelling car that's moving away, why is it that I can still get the signal from the 10,000 watt station while the 1,000 watt signal soon fades. Both signals are EM waves, so why should either fade with increasing radial distance? Don't these signals continue to propagate @ light speed into the solar system and beyond?
 ANSWER:
ANSWER:
Once you are far from the broadcasting antenna compared to
its size, it looks like a point source and the signal drops off like 1/D2
where D is the distance from the antenna. The signal from the 1 kW
station is smaller than that from the signal from the 10 kW station by a
factor of 10. There is a threshold below which your radio cannot process
accurately the information in the signal and the 1 kW station drops below
that threshold first. They do continue propogating as the distance gets
bigger but with ever-decreasing intensity.
The animation on the home page is a catylatic
converter where a CO molecule comes to the platinum surface, rattles
around for a bit, then picks up an O atom and departs as CO2.
 QUESTION:
QUESTION:
I would like to ask another question, this one a variation on the twin paradox in relativity. In this case, instead of twins, let us suppose triplets, Alex, Ben, and Charlie. Alex gets in a spaceship and rockets away from the earth at near the speed of light; Ben gets in another spaceship at the same time (in Charlie's frame of reference) and follows him on the same trajectory at half that speed; Charlie remains on earth. After rocketing for some originally agreed upon distance, Alex turns around and rockets back to earth, again at near the speed of light. After rocketing half of Alex's distance (in Ben's frame), Ben also turns around and rockets back to earth, again at half Alex's speed. Now, as I understand it, in Charlie's frame, Alex is rocketing away and back at near the speed of light, and should therefore experience observable relativistic effects; in Alex's frame, by contrast, Charlie is the one moving; in Ben's frame, however, both Alex and Charlie are moving, but at slightly less than half the speed of light, at which there should be no (non-trivial) relativistic effects. So what happens? It seems that in Charlie's frame, upon the return of his brothers, he and Ben should still be the same age (or close enough as makes no difference), since Ben underwent no observable relativistic effects, but Alex should be younger now, since he did undergo observable time dilation. In Ben's frame, though, it seems like all three brothers should still be the same age, since none of them ever went past about half the speed of light. So how is this apparent paradox resolved?
 ANSWER:
ANSWER:
This is just the twin paradox doubled and there is still
nothing paradoxical. First, read my original
twin
paradox answer to see what I am doing here. I will do it generally
although you could do it for a specific number (e.g. the 8 ly trip at
β=v/c=0.8 for the original answer). One problem with
your question is that if Ben goes half the distance that he measures
Alex going, they will not arrive home at the same (Charlie) time. You have to say that
relative to Charlie the distances are LCharlie for
Alex and LCharlie/2 for Ben and the relative speeds are β
and β/2. Then, Charlie's clock when Alex and Ben arrive will be
TCharlie=2LCharlie/β.
Now, Alex
and Ben both see the distance they have to travel to be length contracted,
LAlex=LCharlie√(1-β2)
and LBen=(LCharlie/2)√(1-(β/2)2).
So the clocks (when Alex and Ben arrive home) will read TAlex=2LAlex/β=(2LCharlie/β)√(1-β2)=TCharlie√(1-β2)
and TBen=(2LBen/β)=(2LCharlie/β)√(1-(β/2)2)=TCharlie√(1-(β/2)2).
That's it.
To do my original
example where LCharlie=8 ly and β=0.8, TCharlie=20
y, TAlex=12 y, and TBen=18.3 y. As you
can see, the time dilation is smaller for Ben with β=0.4, but
certainly not neglibible.
The triplet paradox is resolved!
 QUESTION:
QUESTION:
why can photons make a laser but electrons and protons can't make a laser like beam.
 ANSWER:
ANSWER:
Laser is the acronym for Light Amplification by
Stimulated Emission of Radiation. So, by definition, a
laser emits electromagnetic radiation. There are apparently some methods to
create coherent electron beams, but you would not call them lasers. There is
something called the free electron laser but it uses electrons to create
electromagnetic radiation, not a coherent electron beam.
 QUESTION:
QUESTION:
I have been reading a bit about time dilation and am curious about
the subject. The fact that a clock on the ISS and another on earth
report slight differences in rate of time show that something is going
on. However, I simply cannot imagine that if a spacecraft where to fly
to away from earth traveling near the speed of light and then
immediately return, that they would return to a future earth. It just
does not seem logical. This brings me to my questions: Are there any
other examples of solid proof that time dilates based on gravity and
velocity or is time dilation still a theory based solely on the ISS vs
earth clock example? Also, a more theoretical question, if time dilation
is true, could stasis (hypersleep) be achieved by moving an object near
the sleep of light backward and forward -- basically a extremely high
frequency vibration?
 ANSWER:
ANSWER:
Sorry it does not "seem logical" but that is not surprising
because it is certainly not intuitive. Intuition is the feeling we have
about something based upon experience and our experience does not extend to
very large velocities where time dilation becomes apparent. Maybe some
earlier answers of mine would help you find it more believable: see my
discussion of the
light clock
and the
twin
paradox. Both of these require that you accept that the speed of light
is the same for all observers; if that does not "seem logical", other
earlier answers might help. There are innumerable examples of time
dilation in the real world. Have you ever used a GPS? The way it works,
essentially, is that satellites buzzing around triangulate your position.
Obviously, accurate timing of signals between you and the satellite are
crucial and if corrections in the software were not made for time dilation
in special relativity (speed effects) and general relativity (gravity
effects), a GPS would simply not be accurate enough to be of any use.
Another example is the lifetime of elementary particles, a simple clock. If
some particle is measured to have a lifetime of 10-6 s and has a
speed of 2.4x108 m/s (80% the speed of light), "logic" would
dictate that it will travel a distance of 2.4x102=240 m before
disintegrating, right? In fact, it travels 400 m because of time dilation.
Regarding your idea for hypersleep, imagine the acceleration the sleeper
would have to endure―the resulting force she would experience would crush
her beyond recognition.
 QUESTION:
QUESTION:
I read somewhere that photons carry electromagnetic force. Also
charged particles exchange photons and the momentum of the exchanged
photons appears as force. My question is, from the above description I
can very well visualize repulsion between like charges but how can it
explain attraction between unlike charges?
 ANSWER:
ANSWER:
The idea of photon exchange must not be taken too literally. It is meant as a "cartoon" picture to convey the qualitative ideas of field quantization. For example, you cannot just think of the recoil of the emitting particle which you normally would in classical physics and seems like an easy way to see a repulsive force. The reason is that these photons are necessarily what are called virtual photons, in some sense they do not exist. You cannot observe a virtual photon. It is easy to see that they cannot be real photons, because if the charged particle suddenly spit out a photon, where did the energy needed for the creation of that photon come from? Energy conservation has been violated! However, in quantum physics, it is ok to violate energy conservation by an amount
ΔE and that violation can last as long as Δt as long as ΔE·Δt≤h/(8π)
where h is Planck's constant, about 6.6x10-34 J·s; this is the famous Heisenberg uncertainty principle.
Often in physics simple, qualitative models are good for getting insight but not necessarily good
as a detailed theory. Another example is the Bohr model of the atom: we know that it describes a lot of data very nicely but we also know that the idea of electrons running around in little circular classical orbits is total nonsense in a rigorous model of the atom.
Another example is the often cited "trampoline model" for gravity, that mass
(a bowling ball, for example) attracts other masses (a marble, for example)
because of the deformation it causes in space-time (represented by the
deformed trampoline).
 QUESTION:
QUESTION:
what is coriolis effect
how does it influence earths atmosphere
 ANSWER:
ANSWER:
See an earlier
answer.
 QUESTION:
QUESTION:
Is it possible to make carbon monoxide (carbon MONoxide, NOT dioxide) into a liquid?
 ANSWER:
ANSWER:
Try as I might, I could not find a phase diagram of CO.
However, the Wikepedia entry for CO lists a triple point and critical point, so one
can be confident that liquid and solid phases exist and a rough phase
diagram can be drawn. The data are
T=-205.1
ºC,
P=0.15
atm for the triple point and
T=-140.3
ºC,
P=34.5
atm for the critical point.
I have sketched an approximate qualitative phase diagram to the left. For
comparison, I have also shown, on the right, the phase diagram for CO2.
If you want to make CO vapor into a liquid at atmospheric pressure you would
need to cool it to about -170 0C; to solidify it, you would have
to go down to around -200 0C. (Wikepedia lists the boiling point
as -192.5 0C and the freezing point as -205 0C, so my
rough phase diagram isn't too bad.) Note the very large differences between
the two: the triple point and critical point for CO are both much lower in
pressure and temperature than for CO2.
 QUESTION:
QUESTION:
I remember being taught that if a photon encounters an atom, the atom will absorb the photon only if the photon's energy is exactly the right amount to raise the atom's electrons to one of its permissible states. If the photon's energy doesn't match, then there'll be no absorption and the photon will just pass by.
How exact does the match have to be, really? It can't require a bang-on precise match, because then absorption would never happen -- the photon's energy would always be some tiny fraction off. And if it doesn't have to match exactly, say if the photon has a tiny amount too much energy, what happens to the excess -- conservation of energy says it has to go somewhere.
 ANSWER:
ANSWER:
There are several considerations here. First, a photon does
not have a discrete amount of energy. Second, an excited atomic state does
not have a discrete amount of energy. These are consequences of the
Heisenberg uncertainty principle and discussed in an earlier answer. Therefore, to excite an atom there is a range of
energies which may be added to achieve the excitation. A third consideration
is that when the atom absorbs the photon it recoils; that is, part of the
photon energy goes into the kinetic energy of the atom not into exciting it.
(An interesting exception to this is the
Mössbauer effect
where the whole solid, not the individual atom, recoils resulting in
virtually recoilless absorption). Finally, the atom may well be moving (in
fact it will be moving) before the absorption occurs and so it sees the
photon as Doppler-shifted, again allowing energies different (as seen by
you) from the excitation energy to cause excitations.
 QUESTION:
QUESTION:
The hydraulic brake has brake fluid inside and it could be dangerous if there are air bubbles it it because a part of the pressure is used to compress it. I am baffled by this due to my assumption that the pressure inside a bubble is atmospheric pressure and i quote from wikipedia " the pressure inside 100 nm diameter droplets can reach several atmospheres " in the laplace pressure page. How could the bubbles 'pop' ?
 ANSWER:
ANSWER:
The bubbles of interest are on the order of a mm (10-3 m), certainly not 100 nm (10-7 m). The pressure is probably roughly atmospheric, but when you increase the pressure in the fluid it compresses the bubbles which results in less movement of the brakes at the other end of the line, and a spongy feeling of the brakes.
 QUESTION:
QUESTION:
This is a question about tractive effort of locomotives. I am a model railroader and we have been debating this situation for a while with no clear answer. If there is a locomotive on the track that has 4 driving wheels touching the rails, and the only change you make is to the number of wheels , now 6 driving wheels on the track, will tractive effort go up, stay the same or drop. The argument for staying the same is that each wheel now supports less weight, so tractive effort of each wheel would drop. The argument for tractive effort going up would be that there are more contact points on the rail, so it would pull more.
 ANSWER:
ANSWER:
What drives your train is the static friction between the
wheels and the track. The nature of static friction is that a maximum amount
of force may be achieved before the surfaces slip on each other. This force
Fmax is determined, to an excellent approximation in many
cases, by the nature of the surfaces (steel on steel for your case, I
presume) and how hard they are pressed together (called the normal force N);
Fmax=μN where μ is the coefficient
of static friction, a number determined by the materials. You will note that
this force does not depend on the area of contact. Essentially, adding
wheels adds surface area but, as you note, the force pressing the surfaces
together (namely the normal force which is determined by the weight) is
simply distributed over a larger area. So, the simplest first-order physics
answer is that the same maximum force from the wheels without slipping will
be achieved regardless of the number of wheels. Friction, though, can be a
tricky business and first-order physics does not always work for all
situations. For example, there are
instances where a car
tire can have greater "road hugging" (read increased friction) if the
road-tire contact area is increased. I believe in your case, though, since
the wheels and track are so little deformed by contact, that increasing the
number of wheels will not increase friction provided that the total
mass of the locomotive remains the same. Of course, if you are adding wheels
to an existing locomotive, you are adding mass so you will be increasing Fmax. There is a very easy way to test this. Put the
locomotive (wheels not free to rotate) on a piece track which is attached to
a horizontal board. Gradually increase the angle of the board until the
train slides down. The tangent of the angle at which it starts to slide will
be equal to the coefficient of static friction. If increasing the number of
wheels does not increase the slip angle, there is no advantage.
 QUESTION:
QUESTION:
if we paint an object with any colour, are we painting its elementary particles-electrons, protons, neutrons?
 ANSWER:
ANSWER:
No. You are putting a layer over whatever you are painting
which has the desired color.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Then are the elementary particles of the layer of our desired colour? I actually want to know that how do we perceive colour since most of the spacd in atom is empty.
 ANSWER:
ANSWER:
You misunderstand what makes something appear a certain
color. It happens at the molecular and atomic level. When white light falls
on an object, some is absorbed, some is reflected, some is absorbed and then
reemitted. The colors absorbed, reflected, and reemitted are determined by
the atoms or molecules which are present in the material you are looking at.
Electrons, protons, and neutrons do not have a color because you are not
looking at them; they, themselves, do not emit light which you see. If a
particular object looks red, for example, it is because it absorbs other
colored light more than red light which strikes it. The origin of light is
at the atomic level. When an atom is excited to a higher state, it decays
back down to its normal state. This means that the atom has lost energy and
that energy comes out as light.
 QUESTION:
QUESTION:
I'm not sure if you would consider this an
'off the wall' question (it seems like a 'deceptively simple' type to me), but here it goes: what would be the relative density (to water's 1 (1000 kg/m^3) say) of something with a theoretical
'complete density,' i.e. something with no empty space between mass components (atoms, quarks, etc.) a celestial goo, if you will. Would this be a singularity material or would this be less than singularity? Some sources list a singularity as being infinite density, so, if that is the case, I'd guess relative comparisons might be pointless.
Part of what I am trying to figure out is how deceptive the term "density" actually is; I am thinking it will end up being something like the differential between the Fahrenheit scale and Kelvin. I would also like to know the how much
'more' surface area a 1 meter by 1 meter square of this material would have than the traditional one square meter (of water I guess) of any traditional material. In that case, I figure ewe have always assumed complete density with surface area calculations, but, for some calculations I need to do, I need to know what
'true' surface area is.
 ANSWER:
ANSWER:
Well, you are pretty close to "off the wall" here! First, a
singularity has infinite density and zero surface area. A black hole is
thought to be such a thing. I could quit there since this is certainly the
limit. However, maybe you want something somewhere between the density of
normal matter and infinite density, something which does not depend on what
the material is. If we think about all matter as being composed of
electrons, neutrons, and protons, we can imagine somehow compressing them
all together to make some "primal stuff". Since electrons have very small
mass compared to neutrons and protons, the number you seek is the density of
nuclear matter, that is, the mass of a typical nucleus divided by its
volume; that number is about 2x1017 kg/m3; so, that is
2x1014 times more dense than water. There are
actually, in nature, objects with this density.
Some stars, late in their lifetimes, collapse under gravitational attraction
to this density and the enormous pressure causes electrons to be "forced" into the protons to make
neutrons; they are called
neutron stars.
Regarding your question about area, it really has no meaning because you
cannot have a square meter of something, it always has a volume as well. If
you had a sphere of nuclear matter of radius 1 m, it would have a surface
area of 12.6 m2
and a mass of 8.4x1017 kg. I guess you could imagine a "sheet of
neutrons" with this density and ask what its area was. Taking the radius of
a neutron to be about 10-15 m, the volume of a sheet of area
1 m2
would be 2x10-15
m3
so its mass would be 400 kg. Taking the radius of a water molecule to be
about 10-10 m, a sheet of water of mass 400 kg would have an area
of about 4x109 m2.
 QUESTION:
QUESTION:
While we were studying about atomic structure, our teacher taught us something (I don't remember precisely how was it) about the reason that electron can't be in the nucleus of an atom. She made some calculations and showed that if electron were in the nucleus, it would have to move with a velocity which is greater than that of light. But what about beta decay? Doesn't an electron originate from the nucleus during beta decay? Does it travel faster than light when it originates?
 ANSWER:
ANSWER:
What your teacher was trying to convey is that an electron
cannot be confined in a nucleus, that is, the structure of an atom cannot
include electrons which spend most of their time inside the nucleus. There
is nothing forbidding an electron from ever being in there. In fact, the
wave function of any atomic electron has a nonzero value inside the nucleus
so it spends some (tiny amount of) time inside. I am not familiar with her
"faster than light" argument; usually the uncertainty principle is used
which shows that the energy uncertainty of an electron confined in a box the
size of a nucleus is too large to be consistent with measured atomic masses.
So, you see, your beta decay example does not violate what she taught you
since the electron does not remain inside the nucleus after its creation.
(Be sure to realize that the beta decay electron did not exist before the
decay happened, it was not hanging around waiting to pop out.)

 QUESTION:
QUESTION:
how much negative charge do I accumulate by touching the earth?
Here is how I (tried) to answer this question:
The Earth carries a negative electric charge of roughly 500 thousand Coulombs (according to different sources I've seen). If I touch the Earth I should therefore pick up some of this electric charge (through conduction) and become negative charged. Assuming the earth can modeled as a conducting sphere with radius 6371 km and me as a conducting sphere with radius 1 m, around how much negative charge would I accumulate? The reason I ask is because I'm trying to prove to myself that grounding does indeed render a charged object neutral (i.e. transfers all the object's charge to the Earth). Using the well known equation for two connected conducting spheres with different radii (see Example 3-13 on page 115 in David Cheng's "Field and Wave Electromagnetics, 2nd Ed."), I calculate 0.0785 C, which is way too big and must be wrong.
 ANSWER:
ANSWER:
There is an old joke in physics the punchline of which is
"consider a spherical cow". I like the spirit of your question, but your
approximations are killing you, I think. But, I cannot quarrel with the
earth being approximated as a sphere and approximating yourself as a sphere
is probably ok too. The problem is the assumption that you and the earth are
conductors. If you take your number for net charge you will find that the
surface charge density is about 1 nC/m2. If your answer were
anywhere near right, you would have to get all the charge from around 108
m2 in your vicinity. But it is not free to move around, either on
the ground or in you. Although you are standing in an electric field, caused
by the earth's net charge, on the order of 150 V/m, this field cannot cause
any significant electric charge to flow onto you because you are not a good
conductor.
 QUESTION:
QUESTION:
I've been studying Schrodinger's equation in one dimension as well as wave functions, and I came across the equation
Ae^i(kx-wt) which supposedly gives you the wave function. I know what all the quantities in this equation except for the "A" represent. I've heard that A has to do with boundary conditions, but I've also heard that A must be a complex number. Could you please tell me how to calculate what this A is supposed to be? Nothing I find on the internet or in books tells me how to find A.
 ANSWER:
ANSWER:
This is a kind of technical question for the purposes of this site. Because Schrödinger's equation is linear, if
f(x,t) is a solution, so is Af(x,t) where
A is an arbitrary constant.
That's mathematics. But, for the wave function to be physically meaningful,
we must require
-∞∫∞
ψ*ψdx=1 where
ψ(x,t)=Af(x,t).
So, A is called the normalization constant which, when evaluated from
the normalization integral, allows the interpretation that
ψ*ψ is the probability density.
That's physics. Incidentally, the wave function you specify is not
normalizable over all space and A must be zero. This is because it is
not a physical wave function since it extends over all space with constant
amplitude.
 QUESTION:
QUESTION:
What is fire? I ask this because I recently viewed an exchange on the Internet where someone was crucified for saying that the sun was a big ball of fire. The prominent theme was that the sun's light and heat was from plasma, not fire. That got me thinking: what is fire? Is there a scientific definition? Is the term fire limited to the traditional fires we see where there is combustion with oxygen?
 ANSWER:
ANSWER:
I am not sure there is a scientific definition of "fire". I
would say that fire is the ionized, radiating gas resulting from a chemical
reaction. I would tend to agree with the opinion that the sun is not a "ball of
fire." Certainly chemistry is not the source of energy emanating from the
sun.
 QUESTION:
QUESTION:
Will a non-magnetic metals interfier with a magnetic field when placed next to a super strong magnet?
 ANSWER:
ANSWER:
All materials have magnetic properties. How they will affect
a magnetic field is a matter of degree.
 QUESTION:
QUESTION:
How are protons produced?
 ANSWER:
ANSWER:
Protons are primordial, the universe is composed of mostly
hydrogen which is protons and electrons. Protons can be made in many ways,
usually in beta decay where a neutron decays into a proton, an electron, and
a neutrino.

 QUESTION:
QUESTION:
Last summer I hit a deer while riding my large motorcycle. The combined weight of cycle and load would be nearly 1,000 pounds, and I believe I was going about 65 mph. The deer weighed approx 150 pounds. Potentially how far could have the deer been thrown by the impact? Furthermore, evidence at the scene of the crash suggested that the deer actually rode on the motorcycle for a short time. How much would that have slowed the motorcycle down immiediatly after impact?
 ANSWER:
ANSWER:
It is not clear to me how the deer could both "stick to" ("
actually
rode on") the bike and
then fly off. If it sticks, that is called a perfectly inelastic collision
and you can easily find the speed right after the collision using momentum
conservation. Momentum is the mass times the velocity and the momentum
before the collision must be the same as before: MbikeVbike+MdeerVdeer=MbothVboth=1000x65+150x0=1150xVboth,
so Vboth=65,000/1150=56.5 mph (assuming the deer had no
velocity in your direction). It is much harder to predict what happened
after the collision if they do not stick together. You could only guess, say
maybe you gave the deer a speed of 30 mph going at a 450 trajectory. The distance would then have been about 60 ft.
 QUESTION:
QUESTION:
Hydrogen can be metalized through high pressures to create metastable metallic hydrogen which has been theorized to be present on Jupiter.
Is it possible to use a particle accelerator to cause a collision between two hydrogen atoms and replicate the pressures present on Jupiter and metalize the hydrogen?
 ANSWER:
ANSWER:
No, because an accelerator does not accelerate atoms. Protons are accelerated, not hydrogen atoms.


 QUESTION:
QUESTION:
If a plane, while mid-flight, had an explosion from the wing or rear area, would the debris maintain the exact same momentum as the plane and go forward alongside it, would the debris go in front of the plane, or would the debris go behind the plane when the accident first happens? Me and two friends got on the topic after watching a movie dealing with a plane crash. One friend thinks debris would go in front, the other thinks the debris would maintain precise momentum with the plane, and I'm thinking it would go behind the plane. We'd really love for a physicist to clear up this question for us, thank you so much!
 ANSWER:
ANSWER:
What anything does is determined by the forces on it. A plane
flying in a straight horizontal line with constant speed has four main
forces acting on it: gravity (its own weight); lift which is the force which
counteracts the gravity to keep it flying level, drag caused by the air, and
the forward force exerted by the engines which counteracts the drag to keep
it from slowing down. If a piece of the plane suddenly separates from the
plane, it no longer has any foward force and it no longer has any
significant lift; so, it will start dropping vertically and slowing down
horizontally, falling down from and behind the plane. The falling is
generally more prounounced than the slowing down (gravity usually a greater
force than drag) so there would be a tendency for the piece to appear to
just drop straight down as seen from the plane. (Be sure to realize that the
forward velocity of the piece is approximately maintained so that someone on
the ground sees it moving forward with about the same speed as the plane.)
This is often seen in bombs dropped from a plane. On the left photograph the
drag on the bombs is small so they keep pace with the planes as they drop.
On the right, the bombs have little parachutes to increase drag and so they
fall behind the plane.
 QUESTION:
QUESTION:
Could a beam of light be used to move an object?
 ANSWER:
ANSWER:
Yes. See an
earlier answer.
 QUESTION:
QUESTION:
If some object, at some distance far from the surface of the Earth, but much closer to the Earth than anything else (meaning everything else in the universe is negligible) is at rest initially but then begins accelerating towards the Earth due to gravity, how long will it take to get to the Earth?
I get that the acceleration is a=GM/r^2. And then you can write a as the second derivative of r which would make it a non-linear differential equation but I have no idea how to solve those really. I have taken a differential equations course but it was 3 years ago so I don't remember if we even solved non-linear ODE's ever.
 ANSWER:
ANSWER:
I have solved variations of this problem twice before,
one very recently regarding Coulomb's law
(simply another 1/r2 force) and
the other where the object
was falling into the sun instead of earth. You should read through these
first since I will skip a lot of the detail here. In the spirit of those two
answers, I will take you at your word that the object is "far from the
surface of the earth", that is, r>>Rearth. Hence, it is
just the Kepler problem with an orbit of eccentricity 1 and semimajor axis
a=r/2 and we need to find half the period T. Kepler's third
law states that T2=4π2a3/(GMearth).
Therefore, T/2=π√[r3/(8GMearth)].
For example, if r=100Rearth (which would mean at an
altitude of 99Rearth), T/2=
9x105
s=250 hr.
You can always estimate how much error is made in this approximation
(assuming the earth and objects are point objects going all the way to zero
separation) by calculating the speed v the object arrives with at
earth's surface. Energy conservation gives -GMearthm/r=½mv2-GMearthm/Rearth
or v=√[2GM(1/Rearth-1/r)]. For
the example I did, v=√[(198/100)GMearth/Rearth]=1.1x106
m/s. If the earth were a point mass, the object would continue speeding up.
If it kept going into the earth at a constant speed, the time it would take
to reach the center would be about 6 seconds, enormously shorter than the
time to get to the surface, so the approximation is superb for
r=100Rearth.
 QUESTION:
QUESTION:
When electron transitions between two energy levels it emits a light photon of energy E=h*v. But a photon is a light particle, i.e. it is localized in space. Such is wave packet is made up of many frequencies and not just one. Then how is E=h*v valid?
 ANSWER:
ANSWER:
You are encountering one of the truths of modern
physics―there are limits to what you can know or measure. It all boils down
to the Heisenberg uncertainty principle which can be stated two ways,
energy/time ΔEΔt≈ħ or position/momentum ΔxΔpx≈ħ.
(These are actually inequalities, but this will do for my purposes.) As
you note, a photon really has a superposition of many frequencies and
therefore not a definite energy. The distribution of frequencies is
determined by the time it takes the photon to pass you, so if the photon is
very localized you will have a very large uncertainty in energy whereas if
it is very spread out, you will have a much better-defined energy. But, how
can this be if energy conservation is to hold? Doesn't the photon come from
the atom dropping from one atomic energy to another? The answer is no, the
energies of excited atomic states can not, contrary to what you might have
been taught, be precisely determined. The reason is simply that an excited
state has a lifetime and so to measure its energy you have only that time to
do so and therefore cannot determine its energy precisely. By contrast, the
ground state lives forever (Δt=∞) and it therefore has a well-defined
energy (Δ
E=0).
Any
given photon has an energy equal to what the energy of the particular atom
that decayed had and if you measure many photons with great precision, you
will not get a perfectly sharp line no matter how good your instrument is
but rather observe a broadening of that line. This is called natural line
broadening. Typically, lines are quite narrow, on the order of ΔE/E≈10-7.
 QUESTION:
QUESTION:
I am a physician on an internet mailing list.
Someone asked why it is easier to push fluid into thick skin using a thin 1cc tuberculin syringe (6 cm long for one cc of fluid) compared to pushing that one cc through the same size needle but from a wider bore 3 cc syringe (1cc is marked off along only 2 cm of distance along the hub).
My theory was that one could develop more pounds per sq cm of pressure using the thinner bore plunger than the same pressure expanded over the wider area of the 3cc syringe. I thought the difference between the two was based on the square of the radius of the syringes.
Others argued for something called Poiseuille's equation which described flow through a tube based on the fourth power of the radius.
 ANSWER:
ANSWER:
Poiseuille's equation gives the pressure drop ΔP along a tube
of length L and radius R due to the viscosity μ of the
fluid, ΔP=8μLQ/(πR4), where
Q is the
flow rate. Although I did not do a calculation, common sense tells me that,
since the tubes are not long, the fluid is probably not very viscous, and
the flow rate is very small, that the pressure drop for the 6 or 2 cm is
negligibly small. Your suggestion is the correct one. If you exert equal
forces on the two with your thumb, the resulting gauge pressure in the
thinner syringe will be 9 times greater.
 QUESTION:
QUESTION:
i tried to find the time it would take for two charges to collide
under electrostatic force,realizing simple kinematics won't cut it,tired
to integrate but failed,how is the question done?and how does it differ
from gravitational force??
 QUERY:
QUERY:
You have to define what "collide" means. Since it is a 1/r2 force, if you use point charges the velocity will be infinite when they collide but they will do so in a finite time. Also, what are the initial conditions (velocities, positions), masses, charges.
 REPLY:
REPLY:
My initial question was the time it would take for a 1/r^2,to
collide,for example two bodies lets say 1g,and a charge of 1micro
coluomb,initial at rest attract each other,and collide,I can't use
simple kinematics to solve this question,what shall I do?
 QUERY:
QUERY:
How far apart are they?
 REPLY:
REPLY:
ok,for simplicity 1m apart,is there a general formula than can help?
 ANSWER:
ANSWER:
Whew! I finally have everything I need. This is the Kepler
problem, the same, as you suggest, as the solar system with gravity. You
may want to look at an earlier answer similar to yours. It is very lengthy to work out the
whole problem in detail so I will refer you to a very good
lecture-note document from MIT; I will just give you some of the
necessary results to calculate what you want. First, a brief overview of
two of Kepler's laws:
-
Kepler's laws refer to problems where the force
is of the form F=K/r2 where K is
a constant and the force is attractive. So it could refer to either two
masses or two opposite charges.
-
The first law states that bound planets move in
ellipses with the sun at one focus. This is really only true if the sun
is infinitely massive but the generalization still leads to an elliptical orbit
for each body, both of which move around the center of mass of the two.
Still, the semimajor axis a of the ellipse (which we will later
need) in the center of mass system can be found for any orbit from the
simple equation a=-K/(2E) where E is the energy of
the system.
-
For your case, the particles move in a straight
line toward each other and then turn around and return to their original
positions. This is just the most elongated possible ellipse with an
eccentricity of 1. Of course this would never really be possible in the
real world since the particles would be going an infinite speed when
they "collide". That means we really should do the problem
relativistically which would greatly complicate the problem. Keep in
mind that you are asking an unphysical question requiring point charges
and infinite forces and velocities. But the answer below should be a
good approximation of the time if they have some finite size small
compared to their initial separation.
-
The third law relates the period of the orbit
T to a: T2=4πμa3/K
where μ=m1m2/(m1+m2)
is the reduced mass. In the gravitational problem, K=Gm1m2
and in the electrostatic problem, K=keq1q2
where ke=9x109 N·m2/C2.
For your case, the energy is given since the charges
are initially at rest and separated by some distance S, so E=V(S)=keq1q2/S
and so a=keq1q2/(2keq1q2/S)=S/2=0.5
m; the reduced mass in your case is μ=m1m2/(m1+m2)=10-3x10-3/(2x10-3)=0.5x10-3
kg; and K=kq1q2=9x109x10-6x10-6=9x10-3
N·m2. Finally, the time it takes for a complete "orbit" (which
would correspond to the particles returning to their original positions)
would be T=√[4πμa3/K]=√[4π(0.5x10-3)(0.5)3/9x10-3]=0.3
s. But, the time you want is just half a period, T/2=0.15 s.
To help you visualize the orbits, the figure below
shows the orbits for the two charges when the eccentricity is just less than
1; imagine the orbits getting flatter yet, approaching two straight lines.

 NOTE
ADDED:
NOTE
ADDED:
I got to wondering what the limits of doing this classically
are, that is, how good an approximation my calculation above would be for
some real system. This requires that I determine how close the two charges
would approach each other before their speed v became comparable to
the speed of light c. I will use the same notation as above and write
things classically. If released a distance S apart, then when they
reach a distance r apart energy conservation gives: keq1q2/S=keq1q2/r+�μv2
which results in v=√[(2ke|q1q2|/μ)(1/r-1/S)].
For the case in point, if I solve for r when v=c/10, a
reasonable upper limit for a classical calculation, I get r=4x10-8
m, about 100 times bigger than an atom. Alternatively, we could ask what the
velocity would be for a 1 mm separation, r=S/1000: v=√[(2ke|q1q2|/μ)(999/S)]=1.9x105
m/s=0.00063 c. In either case, I think we can conclude that the time
remaining to complete the half orbit will be extraordinarily small compared
to 0.15 s.
 QUESTION:
QUESTION:
I read recently that Lene Vestergaard Hau stopped a beam of light in its tracks. Isn't this a violation Heisenberg's uncertainty principle as both the velocity and the position of the photon are known simultaneously?
 ANSWER:
ANSWER:
The light is not really so much as stopped as trapped and it
is confined in a Bose-Einstein condensate which is non-zero in size. It
certainly does not violate the uncertainty principle.
 QUESTION:
QUESTION:
If a ship is traveling toward the Earth at a speed of 0.25c from 4 light months out, and they are looking at the Earth and collecting optical images (which at the start would be 4 months old) what would the collection rate be? Would it still be 1 to 1? Or would they be collecting it fast since they are traveling toward the source of the light?
 ANSWER:
ANSWER:
It would certainly not be 1 to 1. I have worked this problem
out in earlier answers. Yours is one of those questions which asks
"how fast do moving clocks
appear
to run at high speeds?" Be sure to note that this is a different
question from how fast clocks run. The speed I normally use for these
situations is 0.8c because the arithmetic comes out easily and I am
here to convey concepts, not arithmetic! A problem virtually identical to
yours (but including also how the ship would observe things going away and
how someone on earth would observe things on the ship) but for 0.8c has been
previously answered;
in that case, a clock on earth appears to run 3 times too fast. For
0.25c, the earth clock would still appear to run too fast but at a
substantially slower rate. If you really need to get a numerical answer, you
can get all the details in my discussion of the
twin
paradox.
 QUESTION:
QUESTION:
It's well established that a rocket propelled spaceship accelerating forward will gain mass as it goes faster and faster. Appreciably so as it approaches light speed. My question is, how does this mass gain manifest itself? That is to say, does it occur by the atomic particles themselves gaining mass (protons, electrons etc.) or do new particles simply pop into existance due to the energies involved? Also, by what mechanism does this occur? How does energy being expelled from the rear result in the addition of mass to the ship and it's contents?
 ANSWER:
ANSWER:
When you think of mass, you think of "amount of stuff". When
I think of mass, I think of inertia. Mass measures how hard something is to
accelerate, and that is inertia. In classical mechanics, inertia does not
depend on on the velocity; a 1 N force will provide exactly the same
acceleration on a mass regardless of how fast it is going. In special
relativity, as an object with mass goes faster, it becomes increasingly more
difficult to accelerate it. In my view, special relativity requires only the
concept of rest mass, its inertia when at rest; beyond that we introduce new
definitions of energy and momentum which then take care of this inertia
issue.
 QUESTION:
QUESTION:
I recently read an article about the world's largest diesel engine.
It is 44 feet tall, 90 feet long and weighs 2300 tons. This engine makes
109,000 horsepower at 102 rpm and is used to power a 1300 foot long
cargo ship. Reading this brought a question to mind. It seems that in
general, the larger a mechanical engine is the slower it rotates. If you
consider a small RC airplane engine, it can rotate up to 20,000 rpm
whereas my car's engine can only rotate at about 6000 rpm. Is there a
physical law, theory, or area of physics that studies and defines the
scaled-strength of materials? More basically why does this seem to be
true?
 ANSWER:
ANSWER:
The acceleration of a mass M moving in a circle of
radius R with speed V is V2/R;
therefore the force necessary to keep it moving in that circle is MV2/R.
Consider two machines, each with the same rotational velocity ω (ω
is in radians per second, but measures the same thing as your RPM) and
one is 10 times bigger than the other. Because V=Rω, F=MRω,
so the force required to keep a gram of some gear or wheel from
flying off the big machine is 10 times bigger than for the small machine. I
believe it is mainly a strength of materials issue although other reasons
are certainly possible depending on what the machine is designed to do.
 QUESTION:
QUESTION:
With all the space junk circling our planet, I wonder how much mass do we have to lose before it affects our orbit around the sun?
 ANSWER:
ANSWER:
First of all, we have not lost that mass, it is still
attached to the earth. Second, the orbit of an orbiting body is independent
of the mass; a 1 gram earth, given the same orbit and speed, would take one
year to go around. For example, there are hundreds of communications
satellites in orbits high above the equator and all have a period of 24
hours, although they have many different masses.
 QUESTION:
QUESTION:
I just read in a book that gravitational force b/w two bodies is due to the exchange of particles called gravitons between them but isn't gravitational force action-at-a-distance force..so from where comes this concept of particles in relation to force,...and how the interactions of gravitons lead to the force gravity?
 ANSWER:
ANSWER:
Gravitons are a speculation, not a fact. Here is a little
background: You would probably characterize electric forces as
"action-at-a-distance" forces. And while, in some sense, that is true, it is
not very satisfying because it is always nice to be able to understand the
mechanism for any force. In the 1940s Richard Feynman and others developed
quantum electrodynamics (QED) in which the electromagnetic field is
quantized, thereby making electrodynamics a field theory compatible with
quantum mechanics. In QED, the quantum of the field is the photon and may be
thought of as the "messenger of the force". It has long been a holy grail of
physics to do the same thing for gravity but nobody has succeded in
developing a theory of quantum gravity; if someone were to succeed, it is
widely accepted that the graviton would be the quantum of the field. There
is already a very successful theory of gravity, general relativity, which
explains the force mechanism as resulting from warping of spacetime.
However, this theory is not compatible with quantum mechanics and, until a
theory of quantum gravity is found, the graviton is purely sepculation.
 QUESTION:
QUESTION:
Convection, conduction and radiation with respect to heat loss in the human body. If 2 equally dressed, equally insulated and body surface area and BMI candidates are sitting in rooms with no air movement, at an ambient temperature of 40 degrees, with the difference that one subjects' room is at nearly 100 percent humidity and the other subject's room is at 35% humidity. Is the saturation of the air and loss of heat by the first subject a function of conductive heat loss? I understand that movement of heat in a liquid or gas state is convection, but would not the high humidity increase the conductive principle of heat loss (and a reason that cold and damp is very uncomfortable)? Or is that still a principle of convection, the gradiant differences in air and body causing a convective heat transfer.... I believe the humidity adds a conductive component... Am I misunderstanding?
 ANSWER:
ANSWER:
Heat loss by conduction of a gas is always very small
compared to convection and radiation. However, here we are talking about
organisms, not just blocks of something or other, and we have evolved to
cool ourselves by evaporative cooling (sweating) which is really important.
Since evaporation occurs at a lower rate when the air is humid, humidity
plays an important role. Still, you are interested in whether conductivity
of air (small though it may be) depends on humidity. The answer is yes, but
the effect happens to be exactly opposite of what you expect―conductivity
decreases as humidity increases as shown on the graph at the right.
 QUESTION:
QUESTION:
If I am driving my car at 70 mph down a straight highway road, and I
drop a brick outside the driver's side window, it would leave the car,
initially, at 70 mph relative to the unmoving ground below. Correct?
However, if I dropped a brick outside my car at 70 mph on the windshield
of another car headed in the exact opposite direction at 70 mph, would
the collective force be the same as if I had dropped a brick on a still
standing car at 140 mph since the other car is headed in the opposite
direction? My knowledge of physics is quite elementary, I'm afraid. But,
if I am thinking of Newton's formula F=M x V, does force change if the
velocity is a relative velocity (ie two objects headed nearly straight
at one another)? And if it does, is it a simple addition problem like I
mentioned above (70mph+70mph= 140mph relatively), or does force get
influenced by gravity/wind friction/absorbing quality of the windshield?
 ANSWER:
ANSWER:
If you look on my faq
page, you will see that there is no way you can calculate the force if
one thing, going speed v, hits something else going with any other
speed. And your expression of "Newton's formula" is wrong, force is mass
times acceleration, not mass times velocity. However, the effect of a 140
mph brick hitting a stationary windshield and the effect of a 70 mph hitting
a windshield approaching it at 70 mph would be the same.
 QUESTION:
QUESTION:
I am a high school physics teacher, and am troubled somewhat by inverse beta decay. From what I gather, it can occur when a proton absorbs an electron antineutrino and an up quark flips to a down quark. It then emits a positron and becomes a neutron. What troubles me is where the energy comes from. Flipping a proton to a neutron requires an input of energy, it seems, because of the mass difference. And then there is the mass and kinetic energy of the positron. Can the electron neutrino possibly supply all of this energy? It seems unlikely.

 ANSWER:
ANSWER:
If you put in the rest mass energies you find that the
neutrino must bring in at least 1.8 MeV of energy. This is not a large
amount of energy for a neutrino. The main source of neutrinos in the
universe is beta decay, so it is to be expected that they would have the
requisite energies to induce the inverse processes. For example, neutrino
spectra from nuclear reactors are shown in the figure above. As you
can see, there are many neutrinos with energies greater than 1.8 MeV.
 QUESTION:
QUESTION:
I am really confused about what Heisenberg principle actually states...why cant the position and momentum can be measured together....cant we measure the position and momentum at any particular instant of time since physics can do anything???
 ANSWER:
ANSWER:
Physics can do anything? Unfortunately, nature has put limits
on how precisely certain things can be determined. The underlying reason for
the uncertainty principle is the fact that there is really no such thing as
a particle. Anything which you might think of as a particle has a dual
reality, it is also a wave. In what way, for example, is an electron like a
wave? Think of a very long wave with some frequency f. It turns out
that the momentum of the wave depends on f. The "position" of this
wave train is uncertain, you will admit because it has some length where it
exists. Now I said earlier that the wave has a frequency f, but in
reality, it has a well defined frequency only if the wave train is
infinitely long. If you want to write an expression for the finite wave, you
find that it is really made up of an infinite superposition of frequencies;
this is called a Fourier transform, decomposing some wave into simple
sinesoidal functions. The most important contributor is the momentum
corresponding to f, but there is a whole distribution of others. So,
you see that the wave has uncertainty in both position and momentum. As I
said above, infinite uncertainty in position will result in zero uncertainty
in momentum. Similarly, if you try to pin down the position by making the
wave train shorter and shorter, you find that the momentum distribution
becomes larger and larger.
 QUESTION:
QUESTION:
Acc. to E=mc2 energy and mass are inter convertible....based on this principle atom bombs have been designed.....so following this equation, a rigid object, say a chair, which is made up of large no. of atoms can be converted into energy which will release a large amount of energy..so can a domestic thing like this be super dangerous!!!!!!!!!!!! if not then why??
 ANSWER:
ANSWER:
It is usually not easy to convert a large amount of mass into
energy. See an earlier answer.
 QUESTION:
QUESTION:
does the terminal velocity in a parachutist's fall occurs two times?
one before opening the parachute
and one some time after opening the parachute Am i right?
 ANSWER:
ANSWER:
The terminal velocity is determined by (among other things)
the geometry of the falling object. In the simplest approximation, what
matters is the cross sectional area of the falling object. So, when the
parachute is opened, the area gets much bigger and the terminal velocity
gets much smaller. If the sky diver has achieved some larger terminal
velocity, she will slow down to the new terminal velocity. However, this
need not be the first time the terminal velocity changed. The sky diver can
orient in a ball or like a down pointing arrow and have a relatively large
terminal velocity or she can fall spread-eagle and slow down. So the
terminal velocity probably changed several times before the parachute was
opened.
 QUESTION:
QUESTION:
How do photons react to heat?
 ANSWER:
ANSWER:
Heat does not refer to some thing. The word heat refers to
energy transfer, and to see more detail you should look on the
faq page. So, heat is not really
something a photon can "react to". (In fact, heat could refer to photons if
radiation is transferring the energy.)
 QUESTION:
QUESTION:
I was just watching a video from IBM and how they were moving single atoms. I heard that atoms are mostly empty space between the nucleus and the electron(s). So when we're looking at a single atoms, what exactly are we looking at? The nucleus or the electrons orbit?

 ANSWER:
ANSWER:
I suspect the video referred to is
"A Boy And His Atom: The World's Smallest Movie".
First, you should appreciate that you are not really "looking" at atoms in
the sense that your eyes are receiving light which comes from the atoms.
Because atoms are much smaller than the wavelength of visible light so you
cannot create an image using visible light. It is popular to refer to an
atom as being mostly empty space, but that is not really true. Because of
the quantum nature of atoms, it is inaccurate to think of the electrons in
the same way we usually think of them when they are free, essentially
point-like particles. Rather, the electrons "spread out" to form a cloud of
charge and mass around the nucleus of an atom. It is true, though, that the
mass density of most of the volume is enormously smaller than the mass
density of the material because most of the mass is in the very tiny nuclei.
When you are far from an atom, it has zero net charge so you do not see any
electric field. But, as you get close to it, you see the negatively-charged
electron cloud as closer to you than the nucleus and so you see a net
electric field which can be measured and recorded. The way this is done is
with a very tiny needle (atomic scale) which is the probe for an instrument
called a scanning tunneling microscope. A computer then takes the measured
electric field and makes a graph of the data and this is what you are
looking at. So, you are looking at a representation of the electric fields
close to the atoms. You can also watch a
video
of how this movie was made.
 QUESTION:
QUESTION:
My question relates to the Hubble constant. As I understand it the further away an object is in the universe from us the greater red shift it exhibits. By looking at how red shifted emission and absorption lines are we can apparently deduce how far away an object is. People always seem to assume that a photon's progress along it's path is loss less. Is it possible that part of the red shift is due to drag along the path the photon travels. Since a photon has no rest mass but has mass simply at lim v>>c it will simply continue at the speed of light but would exhibit a loss of energy that appears as a red shift. Or for that matter part of the red shift. I think my question involves both classical E and M and Quantum mechanics.
 ANSWER:
ANSWER:
Again, I emphasize that I usually do not answer questions in
astronomy/astrophysics/cosmology. I think you are thinking about the photon
in a classical sense, like it is a ball falling through molasses and losing
energy as it goes. But, a photon is an all or nothing thing if it is
traveling in a straight line. Photons can be either absorbed or scattered if
they encounter some interstellar medium, there is no "drag" in the classical
sense. If a photon is absorbed by an atom or molecule in a molecular cloud,
its energy will eventually be reemitted but in random directions not toward
us. If it encounters an atom or molecule, it may be scattered (losing some
energy) but, again, out of our line of sight. Astronomers do need to worry
about this loss of intensity when trying to determine intrinsic brightness
of stars, but this light is lost to us, not red shifted.
 QUESTION:
QUESTION:
I learnt recently that the gravitational field strength which is represented in Einsteins space time fabric is the masses gravitational acceleration. Yet I know that the value of the gravitational acceleration of any mass grows exponentially. Why in the visual representations of the fabric only shows dents (if it were exponential, the visual representations should be an endless dent which approaches negative infinity).
 ANSWER:
ANSWER:
I am having trouble understanding what you are asking. When
you say "grows exponentially" are you referrring to the 1/r2
behavior of the gravitational force? Your "endless dent" would occur only
for a black hole which has zero size. For any larger object, the magnitude
of the force no longer increases like 1/r2 once you are
inside it. For example, the gravitational force is zero at the center of the
earth.

 QUESTION:
QUESTION:
If I person could build wings for themselves like Icarus and fly at 99.999 percent the speed of light, all the way to the Andromeda galaxy, two and a half million light years distant, how much time would pass from their perspective? Would they experience said trip as taking two and a half million years, or would time pass more quickly for them? Would they even be alive upon reaching said galaxy?
Do we even possess the mathematics to work a problem like that out?
 ANSWER:
ANSWER:
What a peculiar way to ask the question most people ask
employing space ships! Of course, there is no air in space so no wings would
be needed to fly and, of course, breathing would be a problem. The painting
of Daedalus and Icarus shown here is the same that I remember from my Latin
book in high school. The important factor in relativity, called the Lorentz
factor γ, is γ =1/√[1-(v/c)2]
which, for your case, is γ =1/√[1-(0.99999)2]=223.6. For
Icarus, time would seem to pass as normal, but he would see the distance he
has to travel shrink by the Lorentz factor: D'=D/γ=2.5x106/223.6=11,180.
7
light years. So, the time that would elapse on his clock would be
11,180.7/0.99999=11,180.8 years. I do not think he would live that long.
Note that only arithmetic was used here, so, yes we certainly "possess
the mathematics to work a problem like that out"!
 QUESTION:
QUESTION:
One of Maxwell's equations is simply a correction to Ampere's law, which states that a magnetic field is induced by a current. Maxwell corrected this to say that a magnetic field can be induced by a both a current and a changing electric field (or more accurately, a changing electric flux).
Here is my concern. Since a current is a movement of electric charges wouldn't these moving charges create a changing electric flux? This electric flux would in turn induce a magnetic field, which becomes the equivalent of saying that the current induced the magnetic field. If the current and the changing electric flux are inducing the same magnetic field, it is in fact the same phenomenon, and Ampere's law doesn't need a correction. By this reasoning Maxwell's correction should instead be a generalization and would simply say that a magnetic field can only be induced by a changing electric flux (where in the case of moving charges the electric flux is caused by the current).
 ANSWER:
ANSWER:
Amp�re's law applies to magnetostatics, all current densities
being steady. And, if you think about currents in wires, there is no net
electric charge and so there is no electric field at all, so even if the
current is changing, there would (according to Amp�re's law) be no electric
field. You are apparently somewhat advanced to be asking this question, so I
put a more detailed explanation here, this being
primarily a site for layman questions.
 QUESTION:
QUESTION:
i am unable to understand a pulley problem
 ANSWER:
ANSWER:
This is a most peculiar problem! However, its solution ends
up being very easy to do (if not to visualize). I will assume that all
pulleys are massless and frictionless and that the string is massless and
unstretchable. I always tell my students when attacking this kind of problem
to "choose a body" upon which to focus and apply Newton's second law. There
are two obvious choices here, the left-side m which results in -T+mg=maleft and the right-side
m which results in -2T+mg=maright. So, we have two equations and three
unknowns; the best you can do is to find the relation between the two
acclerations, 2aleft+aright=3g.
To generate a third equation, choose the left pulley which results in 2T-T=0=T.
So, the only result which works is aleft=aright=g,
both masses in free fall.
I was having a lot of trouble visualizing how this happens, so you I made
a little model and made a movie of it. To see it, go to the
Ask The
Physicist facebook page. (I know, it's not going to win an academy
award, but it satisfied my curiosity!) The two masses, with equal
accelerations, will move equal distances in equal times which then made it
pretty easy for me to make a little model on the floor with strings and
paint cans. Apparently the left pulley moves twice the distance the right
pulley moves in any given time.

 QUESTION:
QUESTION:
If a rogue planet the same size as Earth was about to hit us, would there be a period of weightlessness here before impact from the gravity of the rogue planet?
 ANSWER:
ANSWER:
By "same size" I assume you mean same mass and radius. You
would not be exactly weightless unless you were at the exact point of
initial impact and then only at the instant when you were crushed. The net
gravitational force on you could be calculated fairly easily just by adding
the two vector forces for any configuration of the two planets; it would be
tedious, though. I will do two simple examples. The gravitational force on
you (your weight) is given by W=MmG/R2 where M
is the mass of the earth, m is your mass, R is the radius of
the earth, and G is the universal gravitation constant. I will call
the distance between the centers of the two planets r and assume that
the collision is "head on", that is,
the rogue planet's center is moving directly toward the center of the
earth. Then it is pretty easy to see that if you are standing at the point
of impact, the force F on you is F=W(1-(R2/(r-R)2));
note that the collision occurs when r=2R and F=0 as I
stated at the beginning of the answer. If you were standing on the opposite
side of the earth, F=W(1+(R2/(r+R)2));
now, when r=2R, F=10W/9. The graph to the right
shows the force you would feel on the impact side (black) and opposite side
(red) as functions of r. Note that when r is very large, F≈W.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
What if a rogue planet 2X the mass of Earth was about to collide, would the oceans be pulled from their beds before impact?
 ANSWER:
ANSWER:
I have added a curve for the near side case you ask about. As
you can see, there is a time before impact (when r=2R) when
the force goes negative. That means the net force is pointing toward the
other planet, not earth, so anything on the earth's surface near the impact
point, including the oceans, will "fall up".
 QUESTION:
QUESTION:
If all the galaxies are accelerating away then is nothing an
intertial reference frame? If so, why do Newton's laws work the way they
do?
 ANSWER:
ANSWER:
I am not, as I emphasize on the home page, a cosmologist, so
take what I say with a grain of salt. I do believe, though, that there is no
such thing as an inertial frame of reference and it really has nothing to do
with acceleration. General relativity posits the equivalence of accelerating
frames and frames in a gravitational field, so any frame where there is any
gravitational field is not an inertial frame. Because there is no place in
the universe where there is truly zero field, there are no inertial frames.
Therefore, Newton's laws are false! However, there are many frames which are
very close to inertial and for which they are almost not false. On earth, a
patently noninertial frame, Newton's laws work remarkably well in many
situations. For much of celestial mechanics (calculating orbits of
satellites and planets, for example), Newton's laws work almost perfectly.
Special relativity originally overthrew Newtonian mechanics which does not
work, even in an inertial frame, at very high speeds without serious
modification of definitions of things like linear momentum and energy.
 QUESTION:
QUESTION:
I think I understand that the speed of light is a constant and it is fast (ok non physicist language, but humour me). However, it is only a huge number because of the units we choose to represent it.
 ANSWER:
ANSWER:
The only reason we use units is to have universally agreed upon
"yardsticks". If we had chosen a length standard (call it the baker) such
that 1 baker=108 m, the speed of light would have been c=3
bakers/s. A small number but still a big speed.
 QUESTION:
QUESTION:
I've been trying to write a action sci-fi screenplay, but there is one problem that I can't get my head around.
During the climax, two characters fall from a 91 story building, with the first jumping off, and the second falling approximately 10 seconds later. The second character proceeds to catch up to the first, and they then brawl.
My question is, how much time would pass before they would hit the ground?
 ANSWER:
ANSWER:
There is a good reason you can't get your head around it:
the second character will not catch up to the first! I will give you a
little basic physics tutorial on possible scenarios. For purposes of
computation, I will assume that the height of your building is about 400 m
(about 13 ft/story) and I will approximate the acceleration due to gravity
to be g=10 m/s2.
-
First I will
assume air drag is negligible, that they fall as if they are in a
vacuum. Then the height y1 above the ground of
character 1 is given by y1=400-5t2
where t is the time since he jumped. This tells us that when
character 2 jumps, y1=400-500=-100 m; since y=0
is the ground, he has already hit the ground! The freefall time (the
time when y1=0) from 400 m is about 8.9 seconds and
the speed when he hits the ground will be about 89 m/s=200 mph.
-
So, maybe we just
need to add some air drag. That certainly will be important for speeds
on the order of 200 mph. When air drag is taken into account, you do not
continue speeding up forever but eventually fall with some maximum
constant speed called the terminal velocity; this happens when the air
drag (up) is equal to your weight (down). If your mass is M, your
weight is Mg or, with my approximation, 10M. Let's use M=100 kg (about 220 lb) so
Mg=1000 N. A good approximation
for air drag is F=¼Av2 where A is the
cross sectional area of the falling object and v is the speed. I
will choose A=1 m2 so, if I set F=1000 and solve for
v, I find a terminal velocity of vt=63 m/s=140
mph. The details of the math gets a little complicated here, so I will
give you the results and spell out the details below for anybody
interested. I find that the time that it takes to reach the ground now
is about 10.8 seconds at which time the speed is about 59 m/s. So
character 2 has less than a second to catch up to character 1, obviously
impossible.
-
Finally, I should
tell you that if the two characters are about identical, about the same
size and weight, character 2 will never catch up with character 1
regardless of the height of the building. In the no-air-drag situation,
both have the same acceleration and so their paths never cross. In the
air-drag situation, both have the same terminal velocity so they will
end up having that speed and separated by some constant distance. The
only way to make it happen is to greatly change the cross sectional area
of character 1, for example, give him a parachute!
I am guessing that, if
you want to have any semblance of reality, you will want to rethink your
climax!
 ADDED
DETAIL:
ADDED
DETAIL:
Vertical fall with quadratic air drag is a well-known
problem worked out in any intermediate classical mechanics textbook. The two
results which I used were v=vt√[1-exp(-2gh/vt2)]
and t=(vt/g)tanh-1(v/vt)
for an object dropped from height h.
 QUESTION:
QUESTION:
What is the difference between electric potential(infinity to a point) and potential difference(between two points)?
Why do we need two terms - electric potential and potential difference?
What's the use?
 ANSWER:
ANSWER:
Because of the definition of electric potential, it is always
arbitrary within an additive constant. Therefore, the only meaningful
quantity is the potential at one place relative to the potential at another,
so only potential difference is really of significance. For example, if you
call the potential at one place V1 and that at another
point V2, you could just as well call the potentials V1'=
V1+C and V2'= V2+C
and there would be no change in any physics you do; note, though, that ΔV=ΔV'
because the C subtracts out. However, if you clearly state
where you have chosen the potential to be zero, then the potential
difference between that point and somewhere else is unambiguously
meaningful, and that is what is usually referred to as electric potential.
The electric potential at a point in space is simply the potential
difference between that point where you have chosen zero potential to be.
For example, for any localized charge distribution (not extending to
infinity), it is customary to choose V(r=∞)=0.
 QUESTION:
QUESTION:
For a story I'm writing I have a space station about 500 meters long with a diameter of about 100 meters. How does one figure out how fast the station has to rotate (correct term?) around it's long axis so that it has 1 Gravity around the circumference inside?
 ANSWER:
ANSWER:
If you move in a circle of radius R with speed
v,
there must be a force on you of F=mv2/R where m
is your mass; this force is directed toward the center of the circle. On
your space station, the force would be provided by the walls and you want
that force to be equal to your weight on earth which is W=mg, g=9.8
m/s2 being the acceleration due to gravity. So, that means you
want v=√(gR)=√(50x9.8)=22.1 m/s. The circumference of the
space station is 2πR=314.2 m, so the time to complete one revolution
would be 314.2/22.1=14.2 s; so the rate of rotation would be 1/14.2=0.07
revolutions per second or 4.2 RPM.
 QUESTION:
QUESTION:
�Electron can pass through two holes at the same time without splitting into two.� I read it in a book, is it true? If so, explain it to me.. Please.
 ANSWER:
ANSWER:
This results from wave-particle duality. All particles are
both waves and particles and, if you look for an "electron wave" (and you
will certainly agree that a wave can pass through two holes at the same
time), you will find one. See an earlier answer for more detail.
 QUESTION:
QUESTION:
Can you make your own Northern Lights (Aurora Borealis) in a
Lab?
 ANSWER:
ANSWER:
The aurorae result from electric charges (mainly electrons)
interacting with high-altitude atmosphere. The atoms become excited and then
deexcite and emit light. The laboratory equivalent would be a
gas-discharge tube.
 QUESTION:
QUESTION:
I have a question upon which I have been pondering for a while and it seems increasingly difficult to answer the more I look into it.
I was wondering, what causes fundamental particles to possess a charge? Is it a similar mechanism to the property of mass whereby particles interact with a field of some sort, is it to do with spin, or perhaps something else entirely different?
 ANSWER:
ANSWER:
This is the kind of question―"what causes" the existence of
something in nature―that science often does not or can not address. Electric
charge is that property which allows matter both to create and experience
electromagnetic fields. If particles could not interact via the
electromagnetic force, we would have no atoms, no light. Fundamental
particles have fundamental properties―mass, electric charge, spin, baryon
number, isospin, charm, etc.―which essentially describe how they
interact with other particles in nature. For the most part, these are simply
empirical quantities for which we have no answer as to what "causes" them.
That is not to say that we never find a "cause" as illustrated by the recent
excitement over the Higgs boson; the Higgs field is thought to be the
"cause" of mass. To my knowledge, there is no similar theory proposed for
electric charge.
 QUESTION:
QUESTION:
Am failing to understand a logic of nuclear reactor. (The
questioner refers to this
link.)
There have been 11 nuclear accidents till now. Considering they occurred during a cumulated total of 14000 reactor years of operation (which i dont understand), how would 15000 nuclear reactors cause an accident every month? Please help understand this.. Am getting so confused an restless here!
 ANSWER:
ANSWER:
The rate at which major accidents have occurred since
reactors have been being built is R=11/1.4x104=7.8x10-4
accidents/reactor/year. If you have N reactors, then the rate at
which accidents will occur for those N is NR=1.5x104x7.8x10-4=11.79
accidents/year≈1 accident/month.
 QUESTION:
QUESTION:
I'm wondering what causes the fluctuations that happen in perfect vacuum in quantum physics?
Are they just an inherent part of the universe, or are there theories about what cause them?
 ANSWER:
ANSWER:
Essentially, the Heisenberg
uncertainty principle is responsible. The principle allows energy to be not
conserved if the time is short enough. If we call the time during which
energy is not conserved Δt and the amount by which energy
conservation is violated ΔE, then ΔEΔ
t≈ħ
must be true; here ħ≈10-34 J·s is the rationalized
Planck's constant. For example, suppose that an electron-positron pair at
rest suddenly pops into existence. The total energy of their rest masses is
about ΔE=1 MeV=1.6x10-13 J, so
the time they may exist before disappearing again is
Δt≈ħ/ΔE≈6x10-22 s.
I
guess this does not really answer your question because it tells you how
this can happen, not why it happens. Note that you must obey other
physical principles as well, for example two electrons cannot pop into
existence because it would violate charge conservation because suddenly net
electric charge would appear and there is no uncertainty principle for
electric charge.
 QUESTION:
QUESTION:
My question is about the doppler effect. It is understood that a moving objects sound waves are bunched up in front of it, and elongated behind it, which creates the sound effect that we hear. What is throwing me off is the bunching up of sound waves in front of the object. Why would the sound waves bunch up in front of the object, wouldn't they just
blend together and harmonize? I keep thinking in my mind that the sound difference we here on a moving object is the harmonizing of the sound waves together as the waves get closer to your ear and not that they are just bunched up together.
 ANSWER:
ANSWER:

What does that mean,
"blend together and harmonize"? Harmonize usually means when two
or more sounds blend together. But the source of sound we are talking about
here is a single sound, so harmonizing seems to be inappropriate. Although
most sounds are complex, it is easiest to understand by first assuming that
the sound you are listening to is a single wave with a single wavelength λ and frequency
f which travels with a speed c in still
air. Think of the source sending out the peak of the wave once every 1/f
seconds. So, a peak goes out and then, 1/f seconds later, the next
peak goes out. But, if the source has a speed v, it has moved a
distance x=v/f while the first peak has moved a distance c/f=λ.
Therefore, the distance between peaks, which is the new wavelength λ',
is given by λ'=λ�x=c/f' where you choose -(+) sign if the
source is moving toward (away from) you and f' is the frequency you
hear. So, the waves either "bunch up" if the source is coming toward you and
"spread out" if the source is going away from you. The Doppler effect is
usually expressed in terms of the frequency, f'=f/[1�(v/c)].
[Incidentally, no generality is lost if you consider a more complex wave
form than a simple single-frequency wave, because any complex wave form may
be represented by a superposition (add up a bunch) of simple waves of single
frequencies. Since the new frequency is proportional to the old frequency,
you get exactly the same shape of complex wave but just "bunched up" or
"spread out". This is called Fourier analysis.]
 QUESTION:
QUESTION:
Was killing time on a slow day at work, and involved a coworker in the site. Some time later he ask a question, which might be up the physicist alley. Assuming we had a person seal in a vacuum with a piece of paper and a baseball, if he threw the baseball and then crumpled up the piece of paper and threw it. Would the paper fly as far as the baseball having no friction to affect it, or does gravity rule supreme and bring it to a halt just as well as it does outside a vacuum?
 ANSWER:
ANSWER:
Let's assume that you are throwing both as hard as you
can which means you exert equal forces on them. Also assume that you
exert that force over the same distance for each case which means you do
the same amount of work (force times distance) on each. That means that
they have equal kinetic energies when you release them. But, kinetic
energy is ½MV2
where M is the mass and V is the speed. So, suppose the
baseball has a mass 100 times the sheet of paper; then, if they have equal
kinetic energies, the speed of the paper will be 10 times larger than the
baseball and therefore go 10 farther. Your last sentence makes no sense
because gravity does not "bring it to a halt", it is friction which does
that.
 QUESTION:
QUESTION:
My question relates to electromagnetic radiation waves like light. I don't understand what the wave looks like in three dimensions. Usually I am asked to picture it like a sea wave or an undulating piece of paper but then how could a radio wave be received by many receivers at the same time in many locations out of the plane of the wave?
The other question on waves is why there is a wave at all. What cause the peaks and troughs or the energy to change direction?
 ANSWER:
ANSWER:
If you have a point source on a water surface, you generate
wavefronts that propogate like circles outward (2-dimensional waves). But,
in three dimensions, the wavefronts are spheres and they propogate outward
as shown in the little animation to the right. So really, 2D waves are not
such a good representation of 3D waves. There is "a wave at all" because the
radio antenna creates waves which propogate outward. Most antennas are
directional, that is they do not send out spherical waves but wave fronts
which are more intense horizontally so that energy is not wasted sending
waves into the ground or into space; maybe the waves are more cylindrical
than spherical. The animation to the left shows a cylindrical wave but for a
radio antenna, the cylinder axis would be vertical instead of horizontal.
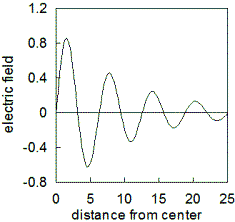
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I
now understand the the wave is promulgated as a sphere (or maybe a cylinder) but I cannot get my head around how that translates into the generally depicted view of the light wave being like an undulating snake. With the sphere analogy surely I would just see arcs of a circle as an observer?
 ANSWER:
ANSWER:
The pictures above show only the wave fronts, which usually
represent the maximum amplitude of the outgoing waves. But the spaces
between the surfaces shown also have the "undulating" waves in them. If you
were to look out along a line and measure the electric field at each point
in space at one time, you would see your "undulating snake". The graph to
the left shows what the results of your electric field measurements along a
radial line would be. The high spots are where you would be crossing the
wave-front surfaces in the 3D pictures above. As time goes on, the whole
wave would move to the right. The reason that the amplitude decreases as you
get farther away from the source is that the waves carry energy and, as you
get farther from the source, that energy gets spread out over a larger area
but the total energy of the wave has to remain constant. (The energy is
proportional to the square of the electric field.)
 QUESTION:
QUESTION:
Suppose a bullet is fired parallel to the ground, due to perpendicular direction of work done with respect to gravity, no work is done against it. Then why does not the bullet fall immediately to the ground as it does when it is not in motion? I have speculated that motion in in dimension reduces the effects of forces of other dimensions. Is there really such a thing in physics? If not, then what is the correct explanation?
 ANSWER:
ANSWER:
First, do not worry about what was happening to the bullet
while the gun was firing it; that is past history and has nothing to do with
what happens to the bullet after it leaves the gun. Newton's first and
second laws tell us that the only reason something will not move in a
straight line with constant speed (or be at rest which is a constant speed
of zero) is if there is a force acting on it. Further, the change in motion
the object experiences is in the direction which the force points. Normally
in elementary physics classes, we neglect the force of air drag (which is a
pretty poor approximation for a bullet) such that the only force is that due
to gravity which we call the weight of the object. So, all the bullet can do
is change its motion in the vertical position because that is the direction
that the weight points. So even though your bullet starts with no vertical
motion, it will fall just as it would if you simply dropped it. In other
words, it will take just the same time to drop to the ground whether you
fire it horizontally or simply drop it. In an
earlier answer, you can see
a strobe photograph where a ball launched horizontally and one dropped fall
vertically the same. In the real world, air drag is not negligible and is a
force which always points in the direction opposite the velocity. This
causes the bullet to slow down in the horizontal direction but to also speed
up more slowly vertically. The figure shows an example where the conditions
allow the whole range of scenerios to play out: because of the air drag, the
horizontal motion is eventually stopped and, because of the interplay
between weight and drag, the projectile ends up falling vertically with a
constant speed called the terminal velocity.
 QUESTION:
QUESTION:
In simple artificial bombardment experiments with alpha particles, how do I determine the correct resulting isotope and if/which particles are emitted? For example, 27Al (a,N) 30P results in the release of a neutron. Some such alpha bombardments result in the release of a protons. How do I determine which will occur? Determining either the remaining particle or the resulting isotope is the issue.
 ANSWER:
ANSWER:
You cannot "determine which will occur." Almost anything will
occur as long as the final products are bound. It is just that they will
occur with different probabilities. A second consideration is, as you
suggest, energetics must be considered. If you subtract all the mass energy
after the reaction from the mass energy before the reaction, you get a
number called the Q-value. If Q<0, the incident particle must bring in that
much energy or else the reaction cannot happen. Here is what we
will need: 1 AMU (atomic mass unit)=931.494 MeV/c2 and a table of
atomic masses (a handy one is here) which gives the atomic masses of
isotopes in AMU. I will do a some examples.
-
Your example: 2713Al(42He,10n)3015P;
MAlc2=26.981538578x931.494=25133.1413
MeV, MHec2=4.00260325413x931.494=3728.4009
MeV, Mn=1.00866491600x931.494=939.5653
MeV, MPc2=29.978313753x931.494=27924.6194
MeV. So, Q=27924.6194+939.5653-25133.1413-3728.4009=2.6425 MeV. So, this
reaction can occur since there is an excess of of energy after the
reaction. There is an additional detail which I will discuss below.
-
Suppose instead we do the (α,p) reaction:
2713Al(42He,11H)3014Si;
MSic2=29.973770136x931.494=27920.3870
MeV, MHc2=1.00794x931.494=938.8901
MeV. So, Q=27920.3870+938.8901-3728.4009-25133.1413=-2.2651 MeV. So, for
this reaction you must bring in an excess of at least 2.2651 MeV of
energy for it to proceed.
-
Finally, a reaction ((p,3n) which bombards with
protons and three neutrons come out) to illustrate my first point above
that the final product must be bound: 63Li(11H,310n)44Be.
44Be would be a nucleus with 4 protons and 0
neutrons and, when you look up its mass you will not find it because it
does not exist; 4 protons will not bind together to make a nucleus, 64Be is the lightest known berylium isotope.
Here is the additional detail mentioned above. The
first example, with a positive Q-value might seem to imply that you can just
have a bunch of Al and He nuclei at rest and they will react to give you a
bunch of neutrons and P nuclei plus a bunch of energy. But, both nuclei are
positively charged and they therefore repel each other. Therefore, you must
give the alpha particles at least enough energy so the two nuclei can
"touch" and interact. I calculate that energy to be roughly 10 MeV for
alphas on 27Al, so your reaction will go for the kinetic energy
of the α-particles of greater than 10 MeV. For the (α,p) reaction, the
kinetic energy must be at least 12.27 MeV.
 ADDED
DETAIL:
ADDED
DETAIL:
Here is the detail of how I estimated 10 MeV. The potential
energy U of two point charges Z1e and Z2e
separated by a distance R is U=kZ1 Z2e2/R
where k=9x109 J·m2/C2 and e=1.6x10-19
C. The projectile, therefore, must start with its kinetic energy equal to U
in order to come from far away to R. I took the size of the
27Al nucleus to be 1.2xA1/3x10-15
m=1.2x271/3x10-15
m=3.6x10-15 m and treated the alpha as a point charge. So, for Z2=13,
Z1=2, U=26x9x109x(1.6x10-19)2/3.6x10-15=1.7x10-12
J=10.4 MeV. I have used 1 eV=1.6x10-19 J. This assumes that the
mass of the Al is infinite compared to the mass of the alpha-particle, but
this is just meant as an order-of-magnitude estimate.
 QUESTION:
QUESTION:
which takes more fuel- a voyage from earth to moon or from moon to earth?
 ANSWER:
ANSWER:
You can get a pretty good idea by just looking at the escape
velocities from the earth and from the moon. From the earth, ve=11.2 km/s
and from the moon, ve=2.4 km/s.
Since kinetic energy is proportional to
ve2,
it would take about 23 times as much fuel to escape from the earth as to
escape from the moon.
 QUESTION:
QUESTION:
If electric fields and magnetic fields both result from the same force (electromagnetic), then why do they interact differently with charged particles?
 ANSWER:
ANSWER:
Because the electromagnetic field is not a vector field, it
is a tensor field. OK, that is kind of technical, so let me try to clarify.
An electric charge at rest will interact differently with the x- and
y-components of an electric field (the Ex will
cause an acceleration in the x-direction, Ey in the
y-direction). The full field may be roughly thought of as having six
components and an electric charge will respond differently to all six. And,
they are all mixed up depending on your motion. If you have a pure electric
field but observe it from a frame moving by it, magnetic fields emerge like
magic.
 QUESTION:
QUESTION:
is there some limit where magnets will no longer cause another to move? If I set a magnet near another and it repels or attracts the other, can I do that an unlimited number of times? If so where does the energy to move that mass come from? Is it infinite?
 ANSWER:
ANSWER:
Of course you can do it an unlimited number of times. Where
does the energy come from? From you since you do work every time you
put the two magnets close together.
 QUESTION:
QUESTION:
We know small amount of matter can be converted into large amount of energy but is the reverse of this possible? Can a large amount of energy be converted into matter and if it is possible has it been observed?
 ANSWER:
ANSWER:
I often get this question. See an
earlier answer.
 QUESTION:
QUESTION:
Astronomy:Astrology :: Physics:Nucleonics ?
 ANSWER:
ANSWER:
It took me a minute to realize that this is one of those
SAT-style analogy questions, "astronomy is to astrology as physics is to
nucleonics?" The answer is that this is false because nucleonics (variably
the study of nuclear energy, or of nucleons or nuclei, or nuclear phenomena)
is a real science and astrology is certainly not. A better analogy would be
astronomy:astrology::physics:psychics.
 QUESTION:
QUESTION:
When you create an electric field or magnetic field is the field established everywhere in space the moment you activate the source? Or does the field build outward from the source?
example:
It is my understanding that when you turn on an electric magnet that the field it creates is created everywhere at once. So something x distance away that reacts to the field will feel it's effects as soon as the magnet is activated and something x + x distance away also feels the fields effects at the exact same moment.
If this is true have there been experiments to prove it and can you site any famous ones?
 ANSWER:
ANSWER:
An electromagnetic field propogates at the speed of light
through a vacuum. This is well known from electromagnetic theory which is
one of the best-understood theories of physics. Also, if an electric field
were to propogate instantaneously, you could send messages anywhere in the
universe instantaneously which is forbidden by laws of physics which are
known to forbid the transmission of information at a speed faster than the
speed of light. So, your understanding of an electromagnet is wrong. But it
might as well be right if you are doing an experiment in a laboratory where
the field appears very close to instantaneously across the room because the
speed of light is so large.
 QUESTION:
QUESTION:
Tritium (1 proton and 2 neutrons) is reasonably stable, with a reported half-life of 12.3 years. Why are there no stable isotopes of hydrogen with more than 2 neutrons?
 ANSWER:
ANSWER:
It is generally not easy to say in a simple way why any
particular isotope is not stable. One of the most important features of the
nuclear force is the pairing interaction. Protons like to pair up with
protons and neutrons with neutrons. So, tritium has a pair of neutrons which
increases the binding energy enough to bind it. A third neutron would find
nobody to pair up with and, in this case, the nucleus would be unbound. You
might think, taking this argument a step farther, that adding a fourth
neutron would result in stability. However, for light nuclei there is a
tendency for there to be equal numbers of neutrons and protons, so the
farther you get fron N=Z, the less stable you get. If you add a
proton to tritium you get an α-particle (4He), one of the most
tightly bound nuclei.
 QUESTION:
QUESTION:
an object is thrown vertically upward on earth with the speed of light . will it leave earth ? My teacher said that it will travel vertically with decreasing c ( gravity ) and reach zero at one point and fall back earth with increasing speed until it reaches earth with the initial speed c , is he right ? Nd what will be the object's route after it starts moving, straight or performing elliptical orbit ?
 ANSWER:
ANSWER:
First of all, site groundrules forbid questions assuming an
object can move with the speed of light. But, since your question is a
little more substantive, I will modify it slightly so that your object may
go any speed less than the speed light, say 99.999999% the speed of light.
The fact is that any object with a speed greater than or equal to the
escape velocity will never fall back down.
The escape velocity from the surface of the earth is only about 11 km/s≈7
mi/s. Your teacher is wrong. The shape of its trajectory if its initial
speed is greater than the excape velocity depends on the direction it is
fired: a straight line if straight up, a hyperbola if shot nonvertically.
 QUESTION:
QUESTION:
Is a brick considered to have a high specific heat capacity?
 ANSWER:
ANSWER:
It is about average for a nonmetalic solid, around 0.2
cal/g·K. Most metals are around 0.03-0.1 cal/g·K, water is 1.0
cal/g·K.
 QUESTION:
QUESTION:
We've all been reading about dark matter and dark energy for some years now and I believe you've said that you (among many others) are not yet persuaded that dark energy and dark matter exist. If matter and energy, as traditionally and conventionally understood, comprise only a very small part of the substance of the Universe, does it follow that classical mechanics, thermodynamics, relativity and quantum theory, etc., correspondingly apply only to that (seemingly) tiny aspect of the world? Is there any reason to think that the laws and theories of physics that humanity has discerned to date would apply also to dark matter and dark energy?
 ANSWER:
ANSWER:
First, a disclaimer: as I state on the site, I am not an
expert in astrophysics, astronomy, or cosmology, so you can take my opinion
with at least a grain of salt or ignore it altogether! I would not say "many
others"! Most astrophysicists, astronomers, and cosmologists talk about dark
matter as if it is surely there but just not directly observed yet. My own
point of view is that I need to see some direct evidence before I accept
that such a thing really is there; there is lots of indirect evidence of
dark matter―the dynamics of galaxies, the time when galaxies first began to
form, to name a couple―but it is altogether possible that we do not
understand gravity as well as we assume that we do. The best theory of
gravity, general relativity, makes many assumptions which are not
necessarily true over really large distances. If this were the case, maybe
dark matter is the 21st century equivalent of the lumeniferous
æther (see the following answer) and is something we are looking for in vain
because there is no such thing. There are lots of good ideas about what dark
matter might be (including WIMPS, for which some
evidence has recently been observed in the observed excess of
high-energy positrons) and I will be happy to accept experimental evidence
when it happens. Dark energy is a different matter in that it has not caused
a search for some "stuff". There is already a place for dark energy in
general relativity, known as the
"cosmological
constant"; in other words, many cosmologists do have the point of view
that dark energy does result from an incomplete theory of gravity.
 QUESTION:
QUESTION:
I believe that Einstein at age 16 did a thought experiment that demonstrated that if one were traveling at the speed of light in a capsule (inertial system) with a light bulb behind you, it would be dark because the light would not travel from the light bulb to you. You would be going as fast as the light leaving the bulb. Thus, you would know how fast you were traveling, and that would be a paradox since the Newtonian model says one cannot know the speed of an inertial system from within.
Did physicists at that time know that the speed of light is constant and not effected by the speed of the source? If so, could you briefly tell me how they had determined that?
 ANSWER:
ANSWER:
There are innumerable anecdotes about the young Einstien's
ruminations; I will not attempt to comment on this aspect of your question
although the more mature Einstein would have surely not suggested that
he could go the speed of light relative to anything else. Regarding what was
known about the speed of light, it was certainly a matter of concern.
Although electromagnetic theory predicted the observed speed of light in
vacuum, light was unique in that it could travel in a vacuum at all.
Basically, when comparing with everything else we knew about waves, most
people could not believe that there was not some medium permeating all of
space through which light traveled and called it the lumeniferous æther.
This is what the now famous
Michelson-Morley
experiment was all about―observing the æther; the
results of that experiment were negative. In later years, Einstein said that
he did not remember whether he had even heard about that experiment when he
formulated special relativity. His arguments for the constancy of the speed
of light were based on electromagnetic theory and the principle of
relativity which states that the laws of physics are the same in all
inertial frames of reference and electromagnetic theory is a law of physics.
 QUESTION:
QUESTION:
If there was an simple molecule in a precise position and its bond energy was X Joules. And you aimed a laser beam at it that produced (1/2)X Joules. Then aimed another laser at the atom that also had (1/2)X Joules. Would the two lasers energies add to overcome the bond energy and split the molecule?
 ANSWER:
ANSWER:
This is called multiphoton excitation and can happen. When
you talk about the energy of the laser beam, it should be the energy of the
individual photons of that beam. So if the sum of the energies of two
photons equals the excitation energy of a process (which would usually be
excitation of an atom or molecule instead of dissociation), the excitation
can proceed. However, the timing is crucial and to have a reasonable
possibility to excite the system with two photons you need very intense
beams to enhance the probability of two interacting "simultaneously".
 QUESTION:
QUESTION:
I am in my powerful rocket. If my orbital speed around the sun was zero and I was the same distance from the sun as the Earth, and my rocket was firing at the exact velocity to hold my position to keep the rocket from from falling towards the sun but no greater, what would my 200 lb Earth body weigh on the rocket ship scales? I am guessing a bit less than 800 lbs. What do you say?
 QUESTION
TO QUESTIONER:
QUESTION
TO QUESTIONER:
What does that mean, "my orbital speed around the sun was zero"? If your speed is zero you are not orbiting. If you are at rest a distance of the earth's orbit from the sun, I would call that hovering. Then you have to calculate the sun's gravitational force on you to know your "weight".
 REPLY:
REPLY:
You are right, I did wish to know my weight when hovering,
 ANSWER:
ANSWER:
The force W which the sun exerts on you (aka your
"weight") is given by W=GMm/R2 where
G=6.67x10-11
Nm2/kg2 is the universal constant of gravitation,
M=2x1030 kg is the mass of the sun, R=1.5x1011
m is the distance to the sun, and m=91 kg is the mass of a 200 lb
weight. If you do the arithmetic, the result is W=0.54 N=0.12 lb.
Quite a bit less than 800 lb! You might be interested in a
similar question where
the questioner wanted to know the time it would take the earth to fall
into the sun if it had no orbital speed.
 QUESTION:
QUESTION:
why can nothing escape event horizon when all it needs to escape
is just to exceed the gravitational force and not to reach the escape
velocity-speed of light in this case- the way rockets on earth do as far
as I know they do not cross the escape velocity
 ANSWER:
ANSWER:
The escape velocity Vescape is defined to
be the minimum speed something must have to escape an object of mass M
to a distance infinitely far away and from a distance R away from M. This is easily shown in classical physics to be given as
Vescape=√(2GM/R)
where G is the universal gravitational constant. Suppose that an
astronomical object exists such that M is large enough and R
can be small enough that Vescape=c, c being
the speed of light. Then R=2GM/c2≡Rs,
this being the Schwartzchild radius. Since no object with mass can travel as
fast as the speed of light, anything inside this radius cannot escape. Also,
light itself inside this radius (for which Vescape
>c)
could not escape either since the speed of light is always equal to the
speed of light. Technically, the calculation of
Vescape is not correctly calculated using classical
physics for either photons or masses going at relativistic speeds, but this
is one of those cases where a correct relativistic calculation gives the
same results as the classical calculation.
 QUESTION:
QUESTION:
I have a 1 ton heavy weight suspended with a rope connected to an electricity generator - I let the heavy weight fall 10 meters - how much electricity can I generate?
I was told it was 10 kW but I do not know how to check.
 ANSWER:
ANSWER:
The question "how much electricity can I generate" does not
have any physics meaning. You have to either ask "how much energy can I get"
or "how much power can I get". And does 1 ton mean 1 metric ton? 1 metric ton is usually written 1 tonne, abbreviated 1 t and is 1000 kg.
If 1000 kg falls 10 m at a constant speed without losing any energy to
friction, the energy delivered will be E=mgh=1000x9.8x10=98,000
Joules of energy. The power generated would be P=E/t where t is the time it takes to fall; power is the rate at which energy is
delivered. For example, if t=20 s, P=98,000/20=4900
W=4.9 kW.
 QUESTION:
QUESTION:
Are electrons and protons respectively attracted preferentially to north or south magnetic fields-?
 ANSWER:
ANSWER:
There are many possible layers to this question:
-
You are probably just asking: "If I put an
electric charge near a magnet, what will happen?" The answer is nothing
because an electric charge only experiences a force in a magnetic field
if it is moving. Either a positive or a negative charge could be either
attracted or repelled from either a north or a south pole depending on
how it was moving.
-
However, electrons and protons are not just
charges but also have magnetic moments, that is, they are like tiny bar
magnets. So, treating them as infinitesimally small, they will
experience a torque in the magnetic field which will cause them to align
with the field so that the N (S) pole of the electron or proton will
point toward the S (N) pole of the bar magnet. Still, there will be no
force.
-
If we allow that the electron or proton magnetic
dipoles are not of zero size, then the nonuniformity of the fields (the
fields get weaker as you get farther away from the bar magnet) will
cause the proton or electron will be attracted to whichever pole it is
closest to.
 QUESTION:
QUESTION:
As you arrive closer to the sun, it would be logical that it would be warmer.
But would the cold vacuum of space be warmer? Wouldn't there have to be some type of surface for the heat from the sun to warm for the area around the sun to be warmer? If the area around the sun is warmer, that would lead me to believe that there is something within the vastness of space that has surface for the radiation of the sun to adhere. And if there are things in the vastness, wouldn't they be detectable by the type of radiation that they absorb?
 ANSWER:
ANSWER:
We usually think of temperature as somehow measuring the
energy of the atoms and moledules. But, if there are no atoms or molecules,
there can still be energy in the form of radiation (photons) and so we can
still assign a temperature to a vacuum as being proportional to the energy
of photons in a unit volume. So, clearly, there will be a higher such energy
density closer to the sun than farther away. To read a lengthier answer to a
similar question,
link here.
 QUESTION:
QUESTION:
How much time would pass on earth if you were travelling 99% light speed for 7 days in your spacecraft?
 ANSWER:
ANSWER:
I presume you mean that your clock, in the space ship reads 7
days. Then, an observer on earth who observes your clock running slow by a
factor of √(1-0.992)=0.14 would observe his clock to read 7/0.14=50 days. Of
course, the time elapsed on earth, as measured by you, would be 0.14x7=0.98
days; each observer measures the other's clock as running slow. However, if
you come back home (twin paradox), you will both
agree that the spacecraft clock was the slower for your round trip.
 QUESTION:
QUESTION:
E=mc squared or so we are told. Can you give an example of energy being converted into matter since presumably energy and matter are interchangeable (at the speed of light)?
 ANSWER:
ANSWER:
The best-known example of energy into mass is
pair production. Another example can be found
in nuclear physics. For example, take a 12C nucleus with 6
protons and 6 neutrons bound together. Because they are bound together, it
will take energy to take the nucleus apart, you must do work. The mass of 6
protons and 6 neutrons is measurably larger than the mass of a 12C
nucleus because E=mc2 and you increase E by pulling
it apart. Your statement "at the speed of light" is meaningless; no matter
can travel that fast.
 QUESTION:
QUESTION:
I have a part (think like a round thick plastic cylinder- it actually is a safety device for heavy trucks that if the air shock system fails the bed of the truck rests on this cylinder).
Similar plastics are used in the part (a toughened with rubber nylon actually) on two exact tests with slight differences that my customer is saying should be NO DIFFERENCE- but I get a failure in one and not the other.
1rst test- 200 lb load at 4.00 feet drop- parts passed
2nd test - 220 lb load at 3.66 feet drop- parts failed
Now I know the "Force" is ~ the same...but could it be failure due to Kinetic Energy change (definition more dependent on mass?)?
 ANSWER:
ANSWER:
I have no idea what you mean by the force being the same, but
it is certainly the force which will determine whether the part fails or
not. Let's start with basics. When an object of mass m moving with
speed v strikes another object and stops, the average force F
to stop it was F=mv/t where t is the time it takes to
stop. Because of Newton's third law, if your load experiences a force F
up,
your part experiences an equal and opposite force of the same magnitude down and
it is that force which causes it to fail. The other thing you need to know
is how fast v an object is moving if dropped from a height h: v=√(2gh)
where g=32 ft/s2=9.8 m/s2 is the acceleration
due to gravity. Scientists prefer to work in metric (SI) units, so I will
need 200 lb (mass)=90.7 kg and 220 lb (mass)=99.8 kg. I calculate the
collision speed of the 200 lb load to be v200=4.88 m/s=16
ft/s and of the 220 lb load as v220=4.66 m/s=15.3 ft/s.
So, the average force over the part experiences over the collisions are F200=442.6/t200
and F220=465.1/t220; assuming the loads
both take the same time to stop, your results are not surprising because the
second test results in a larger force. For example, suppose the loads take
1/100 second to stop. F200=442.6/
0.01=44,260
N=9,950 lb and F220=465.1/0.01=46,510
N=10,456 lb. If you cause the collision time to be longer (for example by
putting a piece of rubber on top of your part) you can greatly reduce the
force on the part during collision.
 NOTE
ADDED, CORRECTION:
NOTE
ADDED, CORRECTION:
I made a mistake above. When the load is stopping, there are
two forces on it, F and its own weight mg, so mv/t=F-mg,
not just F. So F=mv/t+mg. The corrected values
above are F200=442.6/t200+888.9
and F220=465.1/t220+978.0.
In the example where t=0.01 s, F200=45,149 N=10,150
lb and F220=47,488 N=10,676 lb. The conclusion that the
220 lb load results in a larger force on the part is unchanged.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I did made a mistake when I say "force": the customer has the 200 pound weight dropped from a 4 foot height with the end result of 800 foot lbs of energy in one test and in the other test it is 220 lb weight x 3.66 feet in the other test- 800 foot lbs of energy (805 actually).
Are you saying using this kind of "math" for failure analysis is flawed?
 ANSWER:
ANSWER:
The calculation of "energy delivered" is certainly correct
and, indeed, in this case, approximately equal amounts of energy (weight x
height is correct for energy here) have been delivered. But, physicists (and
probably engineers too) tend to think of force as what matters in breaking
something. After all, some of the energy goes into things other than breaking
the part―heat, sound, deformation or damage to load, etc.―but the
force I calculate is certainly applied to the part. In addition, the forces
differ by 5.2% whereas the energies differ by only 0.6%. And, perhaps most
important, you have definitively shown that the analysis method must be flawed
because you actually did the experiment (testing is what science is all
about!) and showed it to be wrong. Maybe the best test would be to put the
part in a hydraulic press and measure the force required to make the part
fail.
 QUESTION:
QUESTION:
Are the protons and or electrons that make up a platinum atom identically the same as the protons in a gold atom with the only difference being the gold atom has one more proton than a platinum atom? This question has intrigued me since I learned that elements that are heavier than hydrogen and helium are products of fusion in supernova explosions. I guess the biggest explosions yield the heaviest elements. In the fusion process, are the individual protons and electrons changed or are they the same?
 ANSWER:
ANSWER:
First of all, only elements heavier than iron require a
supernova to create them. But, the answer to your main question is that any
isolated proton or electron is indistinguishable from any other
isolated proton or electron. The protons and electrons which were used to
make platinum are just the same as those used to make gold or lead or
tungsten or carbon. when the protons are bound together in the nucleus of an
atom, though, they become part of a new system and are changed ever so
slightly. This is evident because if you measure the mass of, for example, a
carbon nucleus which is made of 6 protons and 6 neutrons will not have the
same mass as 6 protons and 6 neutrons. This is because of E=mc2;
since the nucleus is bound together, you must add energy to take it apart
and that causes it to get heavier. To read more about fission and fusion,
see an
earlier answer.
 QUESTION:
QUESTION:
So, in today's science, there is this "Law of Conservation of Energy".
And all motion is supposedly kinetic energy and comes from potential
energy. But I noticed one day that in Newton's three laws of motion,
motion is created not by energy or potential energy, but by an
"unbalanced force". And I remember that fridge magnets can give off
"endless" force apparently without any electrical energy input. So,
wouldn't it be theoretically be possible to break the "Law of
Conservation of Energy" using this "force-energy gap"?
 ANSWER:
ANSWER:
A force alone cannot create energy. The force must act over a
distance, thereby doing work. Let's not use a magnet as an example because
it is sort of complicated because a magnet never does work (see an
earlier answer). Just
consider an object in a gravitational field. If you drop a stone, you would
say that its energy is not conserved which is true; but conservation of
energy applies only to isolated systems, systems on which no external
forces are doing work and clearly the gravity is doing work on the stone,
thereby changing its energy. The other way of looking at this system is that
we can incorporate the work done by the gravity into the problem; this is
called introducing potential energy. Now, you have made the gravitational
field part of the system and the total energy of this system will not
change.
 QUESTION:
QUESTION:
I understand that air has molecules in constant motion and are constantly in collisions with other molecules but what are they traveling through and how much free space is there? I think a better way of posing my question is that say you vacuumed out all of the matter out of a chamber, then introduced some specific small volume of gas. Clearly there are gas molecules in the chamber now but there's got to be empty space through which they can travel, right? Is that a space a vacuum? Assuming my assumptions are true how much of this "free vacuum space" is there in ambient air?
 ANSWER:
ANSWER:
The density of air is about ρ≈1.2 kg/m3.
The mass of a typical air molecule (N2 or O2) is about
m≈5x10-26 kg, so there are about N≈ρ/m≈2.4x1025
molecules/m-3. The approximate radius of an air molecule is about
R≈1.5x10-10 m, so the volume of a molecule would be about
V≈4πR3/3≈1.4x10-29 m3. The
volume occupied by all the molecules in one cubic meter would therefore be
NV≈3.4x10-4 m3 or about 0.03%; the rest,
99.97%, is, as you surmise, vacuum.

 QUESTION:
QUESTION:
So I understand that protons and neutrons are made of quarks. A proton is made of two up quarks and one down quark and a neutron is made from two down quarks and one up quark. I know that much. But there are so many other particles in the standard model. Are there any other large particles we can (or cannot) observe besides protons and neutrons that are composed of quarks or bosons or whatever? I have been wondering this for a while.
 ANSWER:
ANSWER:
There is, of course, no concise answer to your question. The
standard model has numerous particles and some are made of quarks (hadrons)
and some are not (leptons and field quanta). The hadrons which are bosons
(integral spin) are made of two quarks, hadrons which are fermions (half odd
integral spins) are made of three quarks. There are also many "particles"
called resonances which are excited states of the more fundamental hadrons.
The figure to the right which I stole from Wikepedia gives a pretty good
overview, I think. For more detail, read the Wikepedia article on the
standard model.
 QUESTION:
QUESTION:
i have to know that why the mass of bob in a pendulum does not
affect the time of oscillation.....i think it should as the more massive
bob should have more potential energy when string is pulled for
10degrree but at the same time when its moving more air resistance would
also act on it. My book of physics says that the number of oscilllations does not affect the final answer of time period per each oscillation.
as we know that a pendulum should automatically stop moving after some time.
This means that if 100 oscillations are taken then the time per one oscillation should be decreased. I know im wrong as my physics book of GCSE says so but i want to know why im wrong and what part of my staement does not make sense
P.S : please use simple language or formulas(if u
wanna use) as i wont be able to understand complex ones.
 ANSWER:
ANSWER:
Let's get straight what we are talking about. You refer to
air resistance and you note that the pendulum will eventually stop. Of
course, the main reason it stops is air resistance. Any air resistance is
assumed to be negligible in a treatment of the pendulum at your level (9th
grade), so imagine that there is none. Second, your book should tell you
that the pendulum only behaves in a simple way if the angle you start it at
is small; but even 300-400 is sufficiently small for
the standard treatment of the simple pendulum to be quite accurate. However,
your expectation that the air resistance will affect your measurement of the
period is wrong because, to an excellent approximation, the period does not
depend on the amplitude and so one period when you start and the amplitude
is, say, 200, will be almost exactly the same as one period when
the amplitude has decayed down to 50. Given your level of school,
I cannot give a very rigorous explanation for why the mass does not matter.
But, if you can understand resolving a vector into components and know
Newton's second law, that F=ma, then you should follow my
explanation. In the picture to the right you see the forces, mg
and T, which act on m. But we are interested in the
motion of m along its arc and neither T nor the
component of mg perpendicular to the arc can affect that
motion, so all that matters is the component of mg along the
arc which is mgsinθ and this is the force which causes the
mass to accelerate along the arc. So, applying Newton's second law for
motion along the arc, mgsinθ=ma; you will notice that m
cancels out so that a=gsinθ. Clearly the acceleration
will determine the motion along the arc and therefore the period will not
depend on m. But, of course, a real scientest tests his hypothesis.
Go to a park where there are swings and find a little boy and his father
both swinging; you will see that they both have the same period even though
they have very different masses. (Your argument about potential energy is
not valid because, although the potential energy at the top is, indeed,
proportional to m (U=mgh), the kinetic energy at the bottom is
also proportional to m (K=½mv2). So, again,
mass cancels out.) Finally, I should tell you what the period does depend
on: only on the length of the string and the acceleration due to gravity,
T=√(L/g)]/(2π). A pendulum clock will not keep good
time on the moon.

 QUESTION:
QUESTION:
If a rope is threaded through 3 adjacent pulleys and attached to a load at the end what is the mechanical advantage of the system? The rope would go over one pulley under another and over the third at which point it would drop down to the load?
I believe the M.A is 1 because the load is only supported by one line. Everyone else contends that it is three since there are three pulleys. What is the right answer?
 ANSWER:
ANSWER:
The tension in the rope is the same everywhere; call that
T. The bottom pulley (to which the load is attached) has three ropes
pulling up on it, so if you pull with a force T you can lift a load 3T.
Everyone else is right.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
The Pulleys are side by side with the line going over the first pulley, under the second, and over and down the third to the load after the third pulley.
 ANSWER:
ANSWER:
Sorry, I misunderstood. You are correct since now just one
rope is pulling up on the load.
 QUESTION:
QUESTION:
Suppose I built a tubesat (personal hobby sat) and sent it to 193 miles above the earth into orbit. Inside this sat would be a single shot co2 based "air gun" which would fire a single microchip based package approximately the size of a stick of gum into deeper space, hopefully propelling it forever outward. My estimates of package size and air gun capabilities lead me to believe I can shoot the package at as much as 1400 fps or so, thus around 1000mph at launch...
My question is - will it work? Can I "shoot" a tiny package out into space from near earth orbit in this fashion?
 ANSWER:
ANSWER:
The speed of the orbiting satellite is about 7860 m/s and the
speed of your package relative to the satellite is about 427 m/s, so the
maximum speed you could achieve relative to the earth is about 8287 m/s.
Escape velocity is about 11,200 m/s. So the answer to your question is no.
[This is just a rough estimate since the maximum speed of the package would
be tangential to the earth's surface which would require an even higher
escape velocity.]
 QUESTION:
QUESTION:
Why are the ripples formed on the surface of water alwalys circular no matter which type of source has produced it .. i mean if v drop a square or a triangular stone then too v end up getting only circular ripples ??
 ANSWER:
ANSWER:
They are not always circular. Drop an 8' 2x4 in the water and
nice straight waves will come from the long side. But on the corners the
waves will come out rounded where the corners were because of diffraction.
Any feature which is not large compared to the distance between water
waves will exhibit diffraction. So, if you drop a square pebble in the water
it will have approximately circular waves almost immediately because it is
small compared to the distance between water waves. The feature of
diffraction can be understood using Huygen's principle which says the next
wave may be generated by assuming each point on the previous wave behaved
like a point source (making perfect little circles) and then drawing the
envelope of all the little circles. The picture below illustrates that for
the the 2x4. I have only drawn a few of the Huygen's wavelets at the left
end to illustrate how the corners get rounded. As the wave (red) spreads
farther the whole rectangle gets rounder and rounder until, finally when you
are much farther than 8' from the 2x4, it becomes almost perfectly round

 QUESTION:
QUESTION:
Why is it that when you place a metal sphere on a flat magnet, it will
spin real easily in one direction (i.e x-axis)? You can forceably spin
it in other directions, but along that single plane it just spins and
spins?
 ANSWER:
ANSWER:
The sphere becomes magnetized, so it looks approximately like
a bar magnet whose south pole sits on the north pole of the original magnet
(see figure at the right). To turn the ball about the x-axis requires
no torque but to turn it about the y-axis does require a torque.
 QUESTION:
QUESTION:
Yesterday, while traveling on the train, I observed a fly come trough the door, it hovered in the centre of the ile and did not touch the inner cabin of the train. The train began to move and the fly continued to hover exactly where it was, it did not seem to struggle with maintaining the same momentum as the train, it just simply hovered. Can anyone explain to me why the fly was able to maintain the same speed as the train without having direct contact with the cabin?
 ANSWER:
ANSWER:
The fly is hovering in the air. The air moves forward with
the train. However, when the train accelerates forward, you feel like you
are being pushed backwards and have to adjust slightly to keep where you
are. The fly also will have to make a little adjustment to keep from
drifting backward.
 QUESTION:
QUESTION:
Am I right in assuming that any thing travelling north on a rail line
for example, and then wishes to go south on that same rail line, must
stop before going in the opposite direction? If this is the case how is it that a train weigh several hundred tons going 90mph heading north on our rail line meets a bumble bee weighing in at a few grams going south just doing 4mph. They collide What I want to know DOES THE BUMBLE BEE STOP before heading in the opposite direction and if the Bee stops does the train stop?????????
 ANSWER:
ANSWER:
Well, we have the problem that the bee will be smushed upon
contact so various parts of him will have different motions. But I think we
can simplify the situation by assuming the bee to be a point mass. If he
stops instantainously when the train hits him, his acceleration would be
infinite so the force on the bee would be infinite so the force felt by the
train would be infinite. I think we can agree that the bee does not stop
instantaneously. It takes some time for the bee to stop which would mean,
assuming it is a point mass, that the train deforms a tiny bit. So, let's do
a quick example: the mass of a bumble bee is about 1/3 of a gram, say about
3x10-4 kg, and the mass of a freight train is about 107
kg. The bee's speed relative to the train is 94 mph≈42 m/s. Suppose the bee
stops (relative to the train) in one millisecond, 10-3 s; then
his average acceleration is about 42,000 m/s2. So, the average
force on him is ma=3x10-4x42x103=12.6 N.
Because of Newton's third law, this is the same force experienced by the
train, so the train's acceleration would be about a=F/m=-12.6x10-7
m/s2 so the train would slow down by about 12.6x10-10
m/s≈28x10-10 mph. After this the bee would have accelerate up to
90 mph so he would feel a continuing force until he got there, but you get
the idea.
 QUESTION:
QUESTION:
I am trying to estmate the energy of a subatomic particle like a proton,by making the v=c or extremely close to c,but i am having a problem that the momentum is becoming Zero when calculating momentum at relativistc speed ,I my completely making a mistake,or am i missng somethin,
 ANSWER:
ANSWER:
E2=(pc)2+m2c4
where m is the rest mass. Also, p may be written as p=mv/√[1-(v/c)2].
As v gets closer and closer to c, p gets bigger and
bigger until eventually the m2c4 term becomes negligibly small
and E≈pc. So, I guess I do not see where your problem is.
 QUESTION:
QUESTION:
Pertaining to the asteroid that recently exploded over Russia, a television "news" station claimed the asteroid exploded with the same force of 20 atomic bombs... now I understand this space rock did quite some damage, but was it's demise really equivalent to the combined exploding force of 20 nuclear warheads?
 ANSWER:
ANSWER:
Well, its mass was about m≈1.1x107 kg and
its speed was about v≈1.8x104 m/s, so its kinetic energy
was about E≈½mv2≈18x1014 J. The energy
of the Nagasaki atomic bomb was about 1014 J, so 20 is about
right. However, its energy was not all released at once and it is estimated
that the energy of the main explosion was about 4x1014 J, about 4 Nagasaki bombs.
 QUESTION:
QUESTION:
If force = mass x acceleration, how does that factor into something moving at a constant velocity? If it hit something, it would still have force, even though the acceleration is technically zero since there is no change in velocity.
 ANSWER:
ANSWER:
When it hits something it comes to a stop very quickly, therefore has a very large acceleration, therefore experiences a very large force stopping it. Because of Newton's third law, if it experiences a force from what it hit, it exerts an equal and opposite
force on what it hit. It is totally untrue that "�acceleration is technically zero since there is no change in velocity."
 QUESTION:
QUESTION:
as earth behaves as a big magnet and even the sun has its own magnetic field, their magnetic fields must have an attraction or repulsion force that can overcome the gravitational force between them as electrostatic force is much stronger than gravitational force.But earth seems to be effected only by the gravity between it and the sun and not on the magnetic force.Why is it?
 ANSWER:
ANSWER:
It is true that the gravitational force is a weaker force
than the electromagnetic force. This, however, does not mean that any
gravitational force is always smaller than any magnetic force. The earth and
sun each have an enormous amount of mass and therefore quite large
gravitational fields. The force on the earth of the sun's gravitational
field is huge compared to the the magnetic force the earth feels from the
sun. Imagine you are holding a bar magnet in your hand―can you move the
earth with it?
 QUESTION:
QUESTION:
we know that rotation off the earth is 1038miles an hour. Now consider that if I fly a helium ballon or any RC helicopter in space for about 15mins, it must go away from us as if I fly an RC helicopter inside a moving train.....But this doesn't seems to happen as I tried it many times in both the circumstances.Why is that?
If your ans is because the atmosphere of the earth is also rotating about the same speed and it makes the helicopter to stay in the space in the same direction without moving away then my question is can we get the expected situation in the moon where there is no atmosphere?
 ANSWER:
ANSWER:
My answer is that both balloons and helicopters fly relative to the air. In a train, the air moves with the train and the hovering helicopter stays with the train. On the moon, neither will fly without air. But if you have a rocket hoverer, like the
LEM, launch it vertically and it will stay over the same point
above the surface because it started with (and therefore kept) the same tangential velocity as the surface;
you could make a similar argument for launching a helicopter from the ground
on earth.
 QUESTION:
QUESTION:
Gravitational forces affect everything that has mass? Light has mass?
Yes we know this because it is affected by gravity (black holes,
Einsteins test of relativity etc) So if light has mass, and traveling at
the speed of light gives anything with mass infinite mass how is it that
light is not more affected by gravity? Why doesn't light itself have a
black hole gravitational effect if it should have infinite mass? I
 ANSWER:
ANSWER:
Gravity also affects everything without mass also. Particles
without mass must travel at the speed of light, but if they have no mass
they will still have no mass when going that speed. The reason that gravity
bends light is that gravity warps space time so a "straight line" is not
really straight if there is a gravitational field. To read about light being
bent, the equivalence principle, and general relativity, see my
FAQ page. I should add that
gravity is caused not just by the presence of mass but by any energy
density. So, a beam of light will indeed give rise to a gravitational field
although quite weak for any realizable intensity.
 QUESTION:
QUESTION:
I would like to know, at what level of gravity (expressed either as G-Forces or acceleration) would an earthlike atmosphere flatten against the surface.
I do understand that Earth's gravity does flatten the atmosphere against it, and that increasing the gravity would progressively flatten and thicken it more--all things exist on a gradient, after all.
But I am wondering, at what gravity would there be a vacuum, or near-vacuum, at perhaps only six feet/two meters above the surface?
 ANSWER:
ANSWER:
The pressure P as a function of height h may be
approximated by P=P0exp[-Mgh/RT] where P0
is the pressure at the surface, M is the gram-molecular mass of the
atmosphere, g is acceleration due to gravity, T is
temperature, and R is the universal gas constant. Using standard
values for T, R, and M and your value of h=2 m,
P/P0=exp[-
2.54x10-5g].
Now, there is no clear "top" of such an atmosphere, you must choose some
fraction of P0; let's just say
P/P0=1/1,000,000=10-6. Solving for
g,
I find g=5.44x105 m/s2, about 55,000 times
bigger than the real earth.
 QUESTION:
QUESTION:
Even though mars weighs one ninth of earth why does is have 38 percent of earth's gravity?
 ANSWER:
ANSWER:
For a spherically symmetric mass, the gravity at the
surface is proportional to the mass of the planet and inversely
proportional to the square of its radius. For Mars the radius is RM=0.533RE
and the mass is MM=0.107ME, so
MM/RM2=(0.107/0.5332)ME/RE2=0.38ME/RE2.
There is your 38%.
 QUESTION:
QUESTION:
This was part of an answer you gave to a question regarding matter
"You understand wrong: matter can be created or destroyed. There is no such law as conservation of matter." I am afraid that I have to disagree with you there. Matter has always existed and is all around us in some form, seen and unseen. The point I am trying to make is, if you can create matter then you must have had something to start with, you cannot create something from nothing. Neither can you destroy it so that it does not exist, you can only change it. Take a pencil for instance, break it down to its smallest atom or smaller than that, it is still none the less a pencil in another form.
 ANSWER:
ANSWER:
The point is that matter is just a form of energy and energy
without mass can create mass. So matter can be created when there is no
matter. The best known example is pair production where an energetic photon
can interact with an electric field and presto! an electron and a
positron, each with one electron mass, appear. Similarly, mass can be
destroyed and release energy. To read more about that, read the answer just
below yours.

 QUESTION:
QUESTION:
I know Einstein said E=MC2 and basically all mater can be equated to some quantity of energy; then why do we go to the gas station to fill our cars? Why can't we use garbage, which is mass and has energy, to power our cars? How can we convert matter to energy? I know we can burn gasoline to use perhaps 1/4 the heat content in the form of expanding gas to apply pressure to the piston in the engine. Has anyone invented a converter that changes matter to energy yet? We eat food and basically run on sugar which fuels a chemical based process. Any other matter converters?
 ANSWER:
ANSWER:
Most of the energy mankind uses comes from chemistry. Burn
coal or gasoline, for example. When you eat and metabolize food, chemistry
is going on. The energy which is extracted comes from―guess what―mass! For
example, when you burn coal the main thing which is happening is that carbon
is combining with oxygen to form carbon dioxide. One carbon dioxide molecule
has a smaller mass than one carbon atom plus one oxygen molecule. So,
chemistry is the best known example of your "matter converter". The problem
is that an extremely tiny fraction of the mass is converted to energy,
something like 0.00000001%, so chemistry is a very inefficient source of
energy. Now, to get more efficiency we have work not with atoms but with
nuclei of atoms. If a heavy atomic nucleus can be induced to split (fission),
the mass of the fragments is smaller than the mass of the initial nucleus by
an amount much bigger than with chemistry, something like 0.1% which is a
huge improvement over chemistry; this is how nuclear reactors work. Also
from nuclear physics, you can take very light nuclei and make them combine (fusion)
and get like 1% of the mass converted into energy; this is how stars work
and so, you see, solar energy comes from "matter converters" too and so does
wind energy since the sun is the energy which causes winds to blow. If you
want to get 100% efficient you have to go to particle-antiparticle
interactions in particle physics. When an electron and its antiparticle the
positron meet, their mass completely disappears and all the energy comes out
as photons. Did you ever see the Back to the Future movies? Doc came
back from the future where they had invented a small appliance called "Mr.
Fusion" to do what you want, to convert garbage into the huge amount of
energy needed to power the time machine.
 QUESTION:
QUESTION:
What is the closing speed of protons before they collide inside the LHC?
 ANSWER:
ANSWER:
By closing speed I presume you mean what is the speed of one
proton relative to the one it will collide with. The speed v of each
proton at an energy of 7 TeV is v=0.999999991c where c
is the speed of light. The speed u of one
relative to the other is
u=(0.999999991+0.999999991)c/(1+0.9999999912)=0.999999999999999959
5c.
 QUESTION:
QUESTION:
Why any atom having magic numbers(i.e 2,8,20,50 etc.) of nuclides has special stability?(sry for 2 in 1 but i am very curious). How can we determine magic numbers? Is there any specific method to calculate magic numbers?
 ANSWER:
ANSWER:
Nuclei with particular numbers of protons or neutrons are
particularly stable. The origin of these so called magic numbers is very
similar to the noble gases of atomic physics where one has a shell model of
the structure and a closed shell is particularly stable. In the case of
nuclei, it took a lot of work to come up with an explanation for the shell
structure. The shell model for nuclei won a Nobel Prize for Eugene Wigner,
Maria Mayer, and Hans Jensen. The trick was to recognize the importance of
the spin-orbit interaction for nucleons; in atomic physics this effect is
also there but very small. The figure to the right shows how the magic
numbers appear. On the left are the energy levels predicted for a simple
potential well without the spin-orbit splitting. On the right are shown how,
if very strong spin-orbit splitting is introduced, new shells emerge. Note
that the first three magic numbers, up to 20, are explained without the
splitting but not for higher numbers.
 QUESTION:
QUESTION:
If we travel through space at such a great speed on earth why do we not
fall over? If earth stopped moving would everything fall down? Also
(sorry for the 3 for 1 but I've always been curious) if I were on a
train travelling at the speed of light and were wearing a special suit
which enabled me to walk from the front to the back of the train, would
I be travelling faster than the speed of light?
 ANSWER:
ANSWER:
If you are on an airplane going 600 mph, why do you not fall
down? Because velocity has no meaning except with respect to. This is
called the principle of relativity, that the laws of physics are the same
all inertial frame of reference; once you find the laws of physics (which
say, for example that you will not spontaneously fall over if you are
standing on level ground), they are true in any other frame which moves with
constant velocity relative to yours (you do not topple over in any frame).
If the earth were to suddenly stop spinning on its axis, you would fall over
but that is because during the time of acceleration, when it was slowing
down, the earth is not an inertial frame; if you are standing in a bus which
suddenly slammed on the brakes, you would fall down. (Keep in mind that your
question is worded wrong because "stopped moving" has no meaning as I
explained above.) Your third question (shame on you, violating site
groundrules) you can find on my FAQ
page; also note that no train can go the speed of light, but there is no
limit as to how close you could get 99.999999999999999%. [One small catch:
the earth is not really an inertial frame because it is always accelerating
because it spins on its axis and revolves around the sun. These effects may
be seen, but they are very tiny and it is a good approximation to say the
earth's surface is an approximately an inertial frame.]
 QUESTION:
QUESTION:
Wonder if you could tell me what size of spring I would need to fire a ball of mass 200 grams up a slope of 30 degrees for 20 metres?
What would I need to fire a 1KG ball the same distance?
 ANSWER:
ANSWER:
There is no single answer to this because the force a spring
exerts depends on how much it is compressed (or extended). A spring's
stiffness is characterized by its spring constant k where F=-kx.
where F is the force a spring exerts if it is stretched or compressed
by an amound x. The easiest way to address your problem is to use
energy conservation. The energy which is stored in a compressed spring is E1=½kx2 and the energy which a mass
acquires by being lifted a distance y is E2=mgy.
Ignoring any energy losses (to friction, for example), energy is conserved,
E1=E2; ½kx2=mgy
or k=2mgy/x2. In your first question,
m=0.2
kg, y=20sin300=10 m, and suppose you want to compress the
spring by 5 cm=0.05 m, then k=2x0.2x10/(0.05)2=1600 N/m.
For your second question, m is 5 times bigger and since k is
proportional to m, k=8000 N/m. Keep in mind that these are
ideal-case situations and in the real world friction is usually not
negligible, so you should build in a safety factor of probably 2.
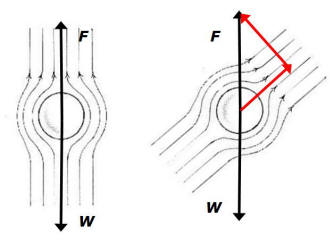
 QUESTION:
QUESTION:
This is a question regarding fluid dynamics. When a ping pong ball is
supported in a tilted airstream it seems to never be in the centre of
the airstream rather slightly below it. Some people have tried to
explain this using Bernoulli's principle but when I think about it the
faster flowing air is at the top so the high pressure at the bottom will
produce a force until it reaches equilibrium in the centre.
 ANSWER:
ANSWER:
When the stream is vertical, the force (F)
which the air exerts on the ball must be vertical and up because the only
other force is the weight (W) which is straight down. Hence,
the net horizontal force from the air must be zero which means the ball must
be right in the center so that a force on the left side will be exactly
cancelled by the force on the right side. This happens only if the air flow
is cylindrically symmetric about the ball. When
the air stream is tilted, the F and W are both unchanged (the air still has
to hold up the weight) but now there must be a component of F
perpendicular to the air stream. The components are shown in red in the
figure at the right. In order to get this component, the ball must move out
of the center of the stream to achieve the asymmetry which will result in
"lift" like an airplane wing. When it drops down lower in the air stream,
the air moves faster over the upper surface than the lower, as you note, and
results in a pressure difference to hold it up.
 QUESTION:
QUESTION:
if two bulbs one of 60w and the other of 100w are connected in
series,then which of the two bulbs will brighter?
 ANSWER:
ANSWER:
I will assume that the resistance of the filaments is
independent of temperature. Light bulb power ratings are made at a voltage
of 120 V. The power is given by P=IV, so I100=100/120=0.83
A and I60=60/120=0.5 A. Ohm's law, V=IR, may
be used to determine resistance: so R100=120/0.83=144
Ω and R60=120/0.5=240 Ω. Now put the two in series and get
a net resistance of 384 Ω which means that the current through them will be
I=120/384=0.31 A. Hence, the voltage across each is V100=0.31x144=45
V and V60=0.31x240=75 V. The power consumed by each is P100=0.31x45=14 W and P60=0.31x75=23 W. So
it looks like the 60 W bulb will be brighter.
 QUESTION:
QUESTION:
Suppose I built a tubesat (personal hobby sat) and sent it to 193 miles above the earth into orbit. Inside this sat would be a single shot co2 based "air gun" which would fire a single microchip based package approximately the size of a stick of gum into deeper space, hopefully propelling it forever outward. My estimates of package size and air gun capabilities lead me to believe I can shoot the package at as much as 1400 fps or so, thus around 1000mph at launch...
My question is - will it work? Can I "shoot" a tiny package out into space from near earth orbit in this fashion?
 ANSWER:
ANSWER:
The escape velocity from a near-earth orbit is approximately
25,000 mph. The speed of a satellite in near-earth orbit is about 18,000
mph. So, the maximum speed of your package is about 19,000 mph. Looks like
it will not escape.
 QUESTION:
QUESTION:
I want to ask question about newtons law of gravitation.i want to ask about this exception.
when we consider 2 like poles of magnet or two bodies having same charge then they do not obey Newtons law of gravitation.because there is a force of repulsion not attraction.then it can become exception to Newtons law
 ANSWER:
ANSWER:
Gravity and electromagnetism are completely different things.
The existence of one kind of force does not make any other kind of force
wrong. The magnets have mass and so they attract each other gravitationally
but, since gravity is such a weak force, it is not noticed. The electric
charges have mass and so they attract each other gravitationally but, since
gravity is such a weak force, it is not noticed. Here is one more example:
suppose a book sits on a table. The table exerts an upward force (repulsive)
on the book. Does that mean there is no gravity?
 QUESTION:
QUESTION:
How do objects (specifically spacecrafts) accelerate in the near vacuum of space? What do they push off of in order to accelerate?
 ANSWER:
ANSWER:
That is not how a rocket works, it does not "push against"
something. Imagine yourself standing on very slippery ice holding a very
heavy rock. If you throw the rock, you recoil in the opposite direction. You
do not recoil because the rocks pushes on the air; the same thing would
happen if there were no air.
 QUESTION:
QUESTION:
I have question about thermodynamics. If you keep the pressure constant, and increase the volume, the temperature should increase or decrease? My thinking is that if you increase a volume, the temperature should decrease, as molecules would collide with walls less, so the average kinetic energy would decrease. But the formula PV=nRT, where nR is constant, if the volume should increase, the temperature should increase. Here I am confused, please help
 ANSWER:
ANSWER:
The ideal gas law, PV=nRT, has four variables―the
pressure (P), the volume (V), the temperature (T), and
the amount of gas (n). So if you change one of these, you can only
find how another changes if you know how the remaining two change. For your
specific question, we can probably assume that n remains constant (no
gas added or removed) but we need to know how the pressure changes. If P
is held constant (called an isobaric process), then T increases if V increases. You cannot assume that increasing
V will decrease T because the collisions of the molecules with the walls determines
P,
not T. Another important kind of expansion is one where the expansion
is done in such a way that no heat can enter or escape the gas; this is
called an adiabatic expansion which is done either in a very insulated
system or very quickly. Without going into any details, TVX=constant
where X is a number between 0 and 2/3, depending on what the gas is.
So, for an adiabatic expansion the temperature does decrease. For example,
if you double the volume of a diatomic gas like oxygen (X=�), T1V�=T2(2V)�,
so T2/T1=1/√2=0.707. Keep in mind that
T must be absolute temperature, so if T1 is room
temperature, about 300 K, T2=212 K≈-610C.
 QUESTION:
QUESTION:
With respect to the speed of sound travelling thru air is 343 m/sec. If the sound wave is coming from a car speeding along at 27 m/sec, then relative to a stationary observer along the highway, is the speed still 343 or 370 (343+27=370).
If the speed of light is constant regardless of the source and is a wave, then doesn't it follow that sound (also a wave) obeys the same principle?
If the speed of light is constant regardless of the
source and is a wave, then doesn't it follow that sound (also a wave)
obeys the same principle?
 ANSWER:
ANSWER:
Sound waves travel with respect to their medium, air. So if
the air is still and you are still, waves from a source propogate toward you
with speed 343 m/s. However, if you are moving (say 27 m/s) toward a source
of sound through still air, then you would measure a speed of sound as 370
m/s. If you are moving away from the source, the speed would be 316 m/s. If
you and the source were at rest and there was a 27 m/s wind blowing from the
source to you, you would measure a speed of 370 m/s. Light is completely
different. The reason that its speed is constant to all observers is that
there is no medium through which it travels, it can travel through a perfect
vacuum. You might look at my FAQ page
to learn more about the constancy of c.
 QUESTION:
QUESTION:
I have been in a debate with a friend on Facebook about a physics problem.
He thinks that in the following scenario, the outcome will be equal to free fall acceleration time. I claim that the Law of Conservation of Momentum will slow it significantly.
There are 11 iron cubes, each 1cm per side.
The cubes are held 1 meter above the one below by a pair of magnets on strings, so when the cube begins to fall, the magnets drop away as not to interfere with the other cubes.
The magnetic force holding each cube in place is exactly equal to its weight, so the slightest touch will make it fall.
The first cube is one meter off the ground, the 11th cube at 11 meters. The magnets holding the 11th cube are pulled away and the 11th cube drops from 1 meter above the 10th cube.
What percentage of free fall time will it take for the 11th cube to reach 1 decimeter above the ground?
Does it make any difference if the collisions are perfectly elastic or perfectly inelastic?
 ANSWER:
ANSWER:
Whoa! This is too convoluted. We do not need to worry about
magnets etc. to answer this question. Each block sits still until
it is hit and then is free. And, it makes a big difference whether we
are talking about elastic or inelastic collisions. And why 11 cubes?
It gets a little tedious and I am not clever enough to get a general
solution for N cubes, so I just chose to use 4 which can be
extended to any number you like. And why ask how
long before the last cube is some distance (1 decimeter?!) above the
ground? Why not just ask when the cube closest to the ground hits the
ground? That is what I will do. Also, let's treat them as point masses,
not 1 cm cubes. Because it is a little involved, I will first outline
the basic equations and then simply summarize the results I found after a couple
of pages of algebra.
-
First the totally inelastic
case. Here when a collision occurs between a mass M with speed U and a mass
m at rest, the stuck-together mass (M+m)
will have a speed u=MV/(M+m) because of momentum
conservation. Since the falling masses slow down with each collision, it
should be obvious to you that the final blob of masses will strike the
floor later than if the top block had simply free fallen to the floor,
so basically, you are right (but, as you will see, only for inelastic
collisions). But let's do the details. If an object
starts with speed v0 and falls a distance h,
its final speed v will be v=√(2gh+v02)
and the time it takes to go the distance h will be t=(v-v0)/g
where g is the acceleration due to gravity. So, the first
block starts with v0=0, falls a distance h=1 m
and acquires the velocity v=√(2g)=4.43 m/s in a time
t=4.43/9.8=0.45
s; it then collides with and sticks to the next block and the two depart
with speed ½(4.43)=2.22 m/s which becomes
v0 for the
next leg of the trip. Continuing this, I find that the next three times
are 0.28 s, 0.23 s, and 0.19 s making the total time to drop the 4 m to
the floor be 1.15 s. With no collisions, the top block would have
acquired a final velocity at the floor of v=√(2x4g)=8.85
m/s making the time to free fall t=8.85/9.8=0.90 s.
-
The elastic case is actually
easier because you are interested in when the lowest ball hits the
floor. Each time one of the balls strikes another, the struck ball
continues down with the speed which the falling ball had and the falling
ball stops momentarily and again falls from rest. Therefore the the
first ball to reach the floor arrives exactly at the same time that a
ball falling without colliding would. In this case, your friend is
correct.
 NOTE
ADDED:
NOTE
ADDED:
It turns out that the questioner was trying, by this
question, to prove that there was a conspiracy involved in the 9/11 World
Trade Center terrorist attack. His reasoning is totally faulty and I disavow
any attempts using my calculations to prove his ideas.
 QUESTION:
QUESTION:
This is a question that I always wanted to know the answer to, but never learned the math to figure out on my own. If I am standing at, or near, the base of something spinning or swinging (like a fan, pendulum etc.) would I be moving slower that the far edge of it? How does the speed change at any given length?
 ANSWER:
ANSWER:
Speed is the distance from the axis of rotation times the angular speed in radians per second. For
example, something spinning at 60 rpm has an angular speed (60
rev/min)(1 min/60 s)(2π rad/1 rev)=6.28 rad/s; so a point 2 m from the
axis has a speed of 12.57 m/s, a point 3 m has a speed 18.84 m/s, and so
on.
 QUESTION:
QUESTION:
I will be filling a pressure vessel (a soda keg) with old, flat tennis balls, then pressuring the vessel to ~30+ psi. The goal is to re-pressurize the old balls so they bounce "like new" (I'm told new unopened tennis ball cans are pressurized to ~17 psi). I believe this will be possible because the rubber membranes of the balls under their felt covers are permeable (to air).
The vessel has a gauge to allow monitoring of the internal pressure. My question is ... as air molecules are forced across the rubber membranes of the balls, would you expect the vessel's pressure reading to remain constant, or would you expect it to drop?
 ANSWER:
ANSWER:
Suppose the pressure is not so large that the balls are
crushed, they maintain their size. When you first pressurize the volume
around the balls, the pressure outside the balls is greater than inside
which, as you suggest, will cause the air to seep into the balls until
the pressure is equalized. The ideal gas equation is PV=CNT where
P is pressure, V is volume, C is some constant, N
is the amount of gas, and T is the temperature. The volume of
the gas outside the balls (which is where you measure pressure) does not
change and I will assume that the temperature does not change. But, the
amount of gas in that volume gets smaller. Therefore the pressure must
get smaller. Incidentally, you will not really be getting the equivalent
of "virgin" tennis balls. The "fuzz", probably all worn off, plays an
important role in the aerodynamics of a tennis ball just as dimples on a
golf ball do.
 QUESTION:
QUESTION:
My questions pertains to the gravitational constant. I'm a theoretical
physicist, so I don't need an obvious answer, and I know the
gravitational force equation works well enough to use but you have more
experience than me so... Shouldn't a universally correct gravity
equation not have a gravitational constant derived from earth? Are we
missing something universally basic about gravity? Even Einstein's
equations use an earth based gravitational constant as part of the
definition. This seems very flawed to me... perhaps you could help me
here?
 ANSWER:
ANSWER:
If there is something which we believe to be a universal
constant, we measure it; we are here so we measure it here. But the
question you ask could be asked of any constant. How do we know that
Planck's constant is the same everywhere (and "everywhen") in the
universe? Once we have the value measured here, and we can measure most
accurately here, we look elsewhere for evidence that physical constants
may vary over distance or time. As far as I know, no evidence has been
found for inconstancy of fundamental constants, but it has been looked
for.

 QUESTION:
QUESTION:
Why do (two dimensional pictures of real) snowflakes ALWAYS have six main points and six sides. General answers on the web refer to the bonding angle of water molecules - 104.5 (doesnt correspond to 60, so dont understand why that would be the determining factor). I presume it has to do with locking in the hydrogen bond, but not sure why the six sided structure would be preferred.
 ANSWER:
ANSWER:
The best answer I can give you is that solid ice has a
hexagonal symmetry as seen in the picture at the right. Here the red
spheres are the oxygen and the grey rods represent the hydrogen. So the
angle does not stay at 104.50 when the water solidifies,
rather opens to 1200. Looking at the picture, the crystal
tends to grow by adding molecules to the outermost oxygen atoms with
only two existing bonds and you can imagine how the snowflake grows.
Also, it is more likely to grow in the direction of the planes of the
hexagons than perpendicular to them, resulting in flat snowflakes.
 QUESTION:
QUESTION:
I was wondering wether a planets diameter relates to it's gravitational
strength and why
 ANSWER:
ANSWER:
There are essentially two things which determine how strong
gravity is at the surface of a planet―what its mass is and what radius
is. The gravitational force is proportional to the mass so that if two
planets have the same radius and one has a mass twice as big as the
other, the more massive planet has twice the gravitational force at its
surface. The gravitational force is inversely proportional to the square
of the radius. So if two planets have equal masses but one has twice the
radius of the other, the smaller planet will have 4 times the
gravitational force at its surface.
 QUESTION:
QUESTION:
Is the acceleration due to gravity always -9.8m/s2 ? I mean when i solve a problem, could i possibly choose the downward direction as the positive direction to make the acceleration turn into +9.8m/s2 ?
 ANSWER:
ANSWER:
You are always free to choose any coordinate system you like.
Indeed, if you choose a y-axis pointing down, the acceleration is
ay=-g where g=9.8 m/s2. [I
generally encourage my students to usually choose +y to be up because
later when you study energy, your textbook will say that the potential
energy of a mass m at a position y relative to the origin
is mgy. It turns out that this is true only for +y
up.]
 QUESTION:
QUESTION:
If a cargo plane allowed 10,000 pounds of cargo and a pilot had to transport 20,000 pounds of birds, would he/she meet the weight limit if there was a way to keep 1/2 the birds flying during the flight?
 ANSWER:
ANSWER:
Let's just suppose we have one bird in a box. That will
illustrate the principle. I always tell my students to "choose a body"
upon which to focus. I choose the hovering bird first. There are two
forces on him, his weight down and a force which the air exerts up on
him up which must be equal to his weight since he is in equilibrium.
Next I choose the air. There are three forces on the air, its weight,
the force of the bottom of the box up, and the force of the bird on the
air. Since Newton's third law says the force of the bird on the air is
equal and opposite the force of the air on the bird, we can conclude
that the box exerts a force up on the air which is equal to the weight
of the bird plus the air. Finally, supposing the box is sitting on a
scale, choose the box as the body. The forces on it will be its own
weight down, the force of the air down on it, and the force of the scale
up on it, so the force the scale exerts up on the box is the weight of
the box plus bird plus air. Therefore the box exerts a force down on the
scale which does, indeed, include the bird's weight. Your 20,000 lb is
what the load in the plane would be whether the birds were in the air or
not. For a much more detailed discussion of a similar problem, see an
earlier answer.
 QUESTION:
QUESTION:
Solve an argument for us please: My friend says that Sound is not part of the Electromagnetic Spectrum and I say it is. I CAN NOT find an answer anywhere on the Internet. What I find is that anything below radio waves in the frequency spectrum is just ignored. Why doesn't the EM Spectrum start at 0hz? If the audio spectrum is ~20hz-20khz then WHEN/WHERE does the EM spectrum start? Wikipedia "Radio Waves" says that radio frequencies can get as low as 3khz. That is an audio frequency, right? So, I'm just looking for a "break point" at which audio becomes radio. And at what point do audio waves become part of the EM spectrum? Is it a definition problem?
 ANSWER:
ANSWER:
Sorry to be the bearer of bad news, but sound is not an
electromagnetic wave. What the wave is is determined not by frequency,
but by "what is waving". Sound is a wave which travels in some medium,
for example air. If there is no medium between you and a source of
sound, you will not hear it. Electromagnetic waves are composed of
electric and magnetic fields which are "waving" and can travel through a
vacuum unlike any other wave. See an
earlier answer. Another difference
is that sound is a longitudinal wave (the air vibrates parallel to the
direction the sound is going) and EM waves are transverse (the electric
and magnetic fields vibrate perpendicular to the direction the wave is
going).
 QUESTION:
QUESTION:
Is this a valid question??? With a valid answer??? It was in a teacher
resource boook. I have my doubts. "It takes 20 million years for the
light of a star to reach Earth. What is the distance between the star
and Earth in light years?? answer: 20 million years".
 ANSWER:
ANSWER:
A light year is defined to be the distance which light
travels, in vacuum, in one year. Therefore, one light year is a measure
of distance, not time as you might guess. Given the way the question is
written and answered, the answer should be either 20 million or 20
million light years, but not 20 million years.
 QUESTION:
QUESTION:
Im trying to
figure out what speed a sphere weighing 4,506 lbs will attain on a 3 degree
grade from complete stop to 95 ft. [After communicating, it is a uniform sphere
of radius 4', rolls, does not slip.]
 ANSWER:
ANSWER:
The easiest way to solve this is conservation of energy.
Let's work in SI units, m=4506 lb=2044 kg, d=95'=29 m, and
R=4'=1.22 m. The energy at the top of the ramp is E1=mgh
where g=9.8m/s2, and h is the height above
the bottom which is h=dsin30=0.052d. The energy
at the bottom where the speed is v is E2=½mv2+½Iω2
where I=2mR2/5 is the moment of inertia and ω=v/R
is the angular velocity. Putting this all
together and solving for v, v=√(0.058gd)=4.07
m/s=13.4 ft/s=9.1 mi/hr. So, you see, the answer to your question does
not depend at all on either the mass or the radius of the sphere, R
and m cancel out as you can show for yourself.
 QUESTION:
QUESTION:
When an object falls to the ground, shouldn't the ground exert a greater force on the object than the weight of the object to stop its motion altogether? Because if the two forces were equal and opposite, they would only cancel the forces resulting in 0 acceleration, but the object should still continue to move at the velocity it had the instant before the force cancellation. (I know it sounds silly for the ground, since it's a solid, rigid body. Maybe it'd be better if you replace the ground for a trampoline and explain it for that).
 ANSWER:
ANSWER:
Yes, the force up by the ground must be greater than the
force down of the weight in order for the object to do what we know it
does, stop. How big the force is depends on how long it takes to stop.
If it is an object hitting a hard surface, it stops very quickly which
means that it requires a large force. If the surface is soft, say a big
fluffy pillow, it takes much longer and the average force is much
smaller.
 QUESTION:
QUESTION:
Figure skating - if you are doing a spin on ice and you leave your arms spread out it creates resistance, if you pull the in towards the body you create less resistance so you spin more easily. How do I express this with mathematical equation in physics?
[The questioner is a 13 year-old high school student with no physics
training.]

 ANSWER:
ANSWER:
While it is true that there is somewhat more air resistance
if your arms are outstretched, you are barking up the wrong tree if you
think this is the reason your spin speeds up when you pull your arms in.
The principle involved here is conservation of angular momentum which is
a topic usually covered late in an introductory physics course, so I
have to give you a little background here. For translational physics
(objects moving without spinning), Newton's second law is perhaps
paramount: the rate at which linear momentum changes is equal to the
force on the object. Linear momentum p is defined to be the mass
m of the object times its velocity v, p=mv. If an
object has no forces on it, the rate of change of linear momentum must
be zero which means that it never changes; this is called conservation
of linear momentum. For a single object, this means that it continues
moving in a straight line with constant speed because the mass will not
spontaneously change. In rotational physics, Newton's second law is
analogous to translational physics: the rate at which angular momentum
changes is equal to the torque on the object. Let's briefly discuss what
the quantities are in translational and rotational physics:
-
Force is what causes an object
to accelerate, change its velocity. Torque is what causes an object to
spin faster (called angular acceleration). Note that it is possible to
exert a force on something without causing a torque, for example,
pushing on a door where it is hinged does not open the door.
-
Linear momentum is p=mv.
Angular momentum is L=Iω, the moment of inertia (see below) times
the angular velocity (for example, revolutions per minute).
-
Mass is the resistance a body
has to being accelerated; a one pound force exerted one second will
cause a much bigger acceleration for a baseball than for a locomotive.
Moment of inertia I is the resistance of a body has to being
angularly accelerated (increased spinning speed). But, monent of inertia
does not just depend on the mass of the body, it also depends on how
that mass is distributed. In the case in point, the figure skater has a
larger moment of inertia with her arms outstretched than not; the same
torque applied to each will result in a smaller spin rate for the
outstretched arms.
-
If you exert no force on an
object, its linear momentum must remain constant. If you exert no torque
on the object which is spinning, its angular momentum must remain
constant.
Are there any torques on the skater who is
spinning? Yes, there is the friction of the skates on the ice and the air
drag on her body, and if she just does nothing she will eventually stop
spinning. However, those torques are small (it would take a pretty long time
for her to stop), so we can say that angular momentum is approximately
conserved. Now, suppose that her moment of inertia with arms outstretched is
Iout and with her arms pulled in is Iin=Iout/3,
and that she is initially spinning with ωout=2 revolutions
per second. Then apply momentum conservation:
That's the whole story. Because
angular momentum is conserved, reducing the moment of inertia results in
increasing the angular velocity.
 QUESTION:
QUESTION:
If an object moves further away from the Earth it gains gravitational potential energy, this means that the energy used to lift the object above the ground is equal to the energy it contains. However there must surely be a point at which the gravitational pull of the Earth is negligible or is outweighed by a different, larger object in space that the object becomes close to. In this case what happens to the gravitational potential energy it had originally from the Earth? It cannot disappear as energy is not created or destroyed but surely it is not still there if the Earth has no pull on it or if a different object such as a planet or star is giving it a different amount of gravitational potential energy?
 ANSWER:
ANSWER:
Let's restrict the discussion to an "earth-only universe"
because other objects will just complicate the situation and cloud the
basic principles needed to understand. Once you understand the two-body
problem, you can simply add other objects, it just makes the potential
energy function more complicated but all the potential energies can be
added up algebraically. As you lift the mass farther and farther away
from the earth, the force gets smaller and smaller and so you add less
and less energy with each meter you lift it and, eventually you might
say that you are adding so little energy by lifting it further that you
decide any additional energy will be negligible. But even if you only
add 10-10 J of energy for the rest of your life, you still
are adding energy. But, the force never completely disappears because
the universe is not infinitely large. So, no matter how far away you
are, when you let go of that mass it will accelerate back to earth and
all that potential energy you gave it will eventually (maybe in millions
of years) be converted back into kinetic energy. No energy ever
"disappears".
 QUESTION:
QUESTION:
I was working on a ship and was down in one of the holds cleaning out the bilges. The hatch cover was closed. No sunlight was entering the hold except for that coming through eight 1.5 inch diameter holes spaced out on the hatch cover. The eight holes cast eight bright circles of light on the deck 70 feet below the hatch cover, creating eight perfectly focused images of the clouds passing overhead. I get that part - pinhole cameras. However, after a couple hours when my eyes were well adjusted to the dark, I noticed another optical effect while sitting down there taking a break. About 25 feet above the hatch cover was parked the boom of a crane, running diagonally across the cover. When my eyes adjusted, I saw a perfect shadow of this crane on the deck of hold, a dimmer version of the shadow that would be seen if the hatch cover were to be opened. In no way was there a regular lay-out of the eight holes in relation to the crane boom. There were not eight different shadows - only one that somehow must have been a composite. Is there a name for this effect?
 ANSWER:
ANSWER:
Here is what I think is happening. Presumably, since you talk
about shadows, it was a sunny day. The eight bright spots you see on the
floor were eight separate images of the sun formed by your eight
"pinholes"; the clouds you saw were clouds passing directly in front of
the sun. As a check, I would expect that the diameter of these images
would be about 7" since the angle subtended by the sun in the sky is
about 0.50, so d≈70'(12"/1')x0.50x(π/1800)=7.3".
But, the sun is only a tiny amount of the whole image formed by each
pinhole; the whole rest of the sky is there but at a much lower
intensity. The crane is part of that bigger image for each pinhole and I
suspect there are really eight images which are pretty much overlapping
because the spacing between pinholes is probably small compared to the
size of either the crane or its shadow. I also think we should call the
shadow an image instead.
 QUESTION:
QUESTION:
wanted to ask that when we say that for e.g i weigh 50kg is that my mass or my weight There is a difference because on earth mass X10=my weight and if 50kg is my mass then why people say that i weigh 80kg or 70kg or50kg or so..........?
why dont they say that this is my mass
and i weigh 500newtons
please explain thi to me!
 ANSWER:
ANSWER:
In physics, you are completely right, a mass of 50 kg has a
weight of 500 N (for g≈10 m/s2). In everyday life in
most of the world, you buy 1 kg of fish, not 10 N of fish. That is just
the convention and it works fine as long as you are at the surface of
the earth because the weight is proportional to the acceleration of
gravity. In countries where weights are expressed in lb, you are
actually buying 1 lb of fish; but in those countries there is confusion
as to what the mass of the fish is. The mass is W/g=1
lb/(32 ft/s2)=0.031 lb·s2/ft≡0.031 slug.
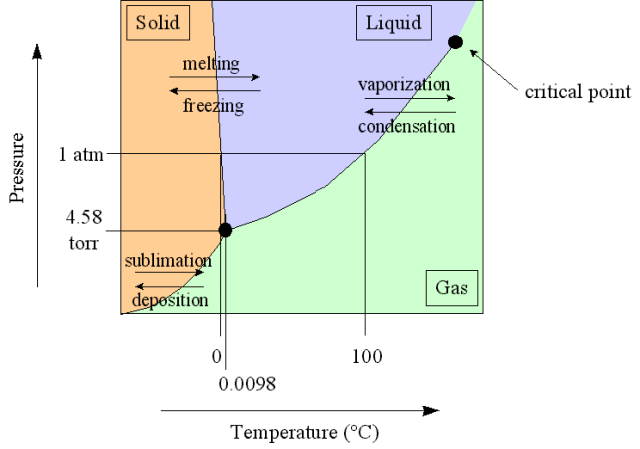
 QUESTION:
QUESTION:
What would happen if we were to compress a gas's atoms so tightly that they could no longer flow freely to be a gas would it change forms into a solid?
 ANSWER:
ANSWER:
It depends on what the gas is. Each material has its own phase diagram which shows what happens as pressure and temperature are changed.
As an example, the figure to the right shows the phase diagram for
water. You can see that at temperatures above about 00C
increasing the pressure on a gas at constant temperature (which is what
you would do to "compress
a gas's atoms"), you create a liquid (called a phase change) If you have
temperatures below
00C and very low pressures, you
can have water in a vapor state and, if you increase the pressure, you
will cause a phase change to solid water (ice).
 QUESTION:
QUESTION:
Im a young student of class 8th here's what i want to ask If two
objects, one with bigger mass(but same surface area,which means air
resistance will be same) and one with smaller mass are dropped from air
which one will fall first? if the same objects(with same material and
size, which means friction will be same) are slided from a ramp which
one will reach down first? if same force is applied to both the objects
(friction and air resistance is same) which one will speed up more? In
my book it is written "in fact, the mass of an object does not affect
how an object speeds up under the pull of gravity" i dont think its
right(book is Heinamann Science 3) Do you agree? i dont. Please explain
this to me as im very serious and anxious about it and use simple
language and formulas and no complex formulas which i wont understand as
im only 14.
 ANSWER:
ANSWER:
When you say "air resistance will be the same", you are
neglecting that the air resistance will depend on velocity, not just
surface area. An often excellent approximation to the air resistance
force F on an object of cross section A moving with a
speed of v is F=¼Av2. When an object is
falling, there are two forces on it, its own weight mg down and
the air resistance F up. If you think about it, the object will
stop speeding up when these two forces have equal magnitudes, mg=¼Avt2
where vt is called the terminal velocity, the fastest
that the object ever goes when free falling. So, vt=2√(mg/A)
and you can see that the bigger m is, the faster a free-falling
mass can go; therefore, the more massive object will win a race with a
less massive object. When your science book says that "the
mass of an object does not affect how an object speeds up" it means that
there is negligible air resistance. Similarly, for the race on the
incline, the more massive should win the race because its terminal
velocity is larger. You could have found many earlier answers on these
subjects on my FAQ page, see 1
and 2.


 QUESTION:
QUESTION:
I teach a self defense course. I am
trying to explain to my students that a 230 grain bullet moving at 850
ft per sec not stop a 200 lbs person running at them at full speed. If i am correct or not could ypu please put it into terms that i could use.
 ANSWER:
ANSWER:
The concept you want to use here is momentum conservation.
Momentum is the product of mass times velocity and the total momentum of
a colliding system must be the same before and after the collision. The
one subtlety here is that if the momentum of a 2 lb mass moving
300 ft/s north is 600 lb·ft/s, then a 2 lb mass moving 300 ft/s
south
has a momentum of -600 lb·ft/s. I will use lb to measure mass and ft/s
to measure velocity, so you have to
be sure you get all the units the same to make any sense: 230
grain=0.033 lb. You say "full speed" so I will use 30 ft/s to be the
person's velocity, which would correspond to a 10 second 100 yard dash.
So, the momentum before the bullet strikes (and lodges in) the man is
200x30-0.033x850=5972 lb·ft/s. (Notice the - sign on the momentum of the
bullet since it and the man are going in opposite directions.) After the
bullet lodges in the man the momentum is 200.033xV where V
is the velocity of the man (plus bullet) after he is hit. Setting the
momenta before and after equal and solving for V, V=5972/200.033=29.9
ft/s. So, you see, the man loses almost no velocity at all due to the
bullet. If you hit his head or his heart he might stop running but it is
certainly not the impact with the bullet which stops him. A qualitative
way to put this is that while the bullet has a speed about 30 times
greater than the man, it has a mass almost 7000 times smaller. Related
to that, when you see a movie in which a character is sent flying
backward by the impact of a bullet, it is total nonsense and will not
happen in real life.

 QUESTION:
QUESTION:
This is not a homework question. It's for an op-ed I'm writing about the pounding offensive football players take from ever-larger defensive players.
What force would a 325 lb. object going 18 mph exert on a 215 lb. object going 20 mph? It would seem that if the 215 lb. object was stationary, the force would be 5,909 lbs. (F = MxA), but that seems way off.
 ANSWER:
ANSWER:
I have answered questions like this many times but every now and
then it is worthwhile to answer it again. There is absolutely no way you
can compute a force from the information you have given. When one object
collides with another, Newton's third law requires that the force one
exerts on the other is of the same magnitude (and opposite direction) as
the force the other exerts on the one. So both players will experience
the same force. That is not the same as saying that both incur the same
damage which would depend on the details of the collision. To determine
what the forces during collision are, you must know how long the
collision lasts. One simplification is that football tackles are usually
inelastic, that is, the two are stuck together after the collision. The
units you use (English) are much harder to do calculations with than SI
units, so I will convert units first and then convert back in the end:
325 lb=147 kg, 215 lb=98 kg, 18 mph=8 m/s, 20 mph=9 m/s. When they
collide, momentum (which is mass times velocity) must be conserved:
147x8-98x9=(147+98)v, v=1.2 m/s, where v is the
velocity after the collision. I assume that you want them to be going in
opposite directions when they collide which is the origin of the
negative sign for the momentum of the 98 kg running back. Now, you want
to know what the force on the 98 kg running back is. An alternative way
to write Newton's second law is F=rate of change of momentum
(which is the same as F=ma and the way Newton actually wrote it).
How much did the momentum (which I will call P) change during the
collision? Momentum change=C=Pfinal-Pinitial=98x1.2-(-98x9)=1000
kg·m/s. Now, the force is F=C/T where T is the time
the collision lasted (which was the main piece of information missing in
your question). For example, if the collision lasted 0.3 s, F=1000/0.3=3333
N=749 lb where "N" is Newtons, the SI unit of force. Note that the force
is positive which means it is in the direction opposite of the running
back's initial velocity, as you would expect. If you were to do the same
calculation for the 325 lb player, you would find that F=-749 lb.
The way to reduce the pain (force) is to lengthen the time of collision
which is the function of padding; when you fall on a mattress it takes
much longer to stop than when you fall on concrete. [If you want to do
some calculations yourself, you might find the free unit conversion
program CONVERT
helpful.]
 QUESTION:
QUESTION:
does the amount of force(i.e the amt. of RECOIL that a gun experience) require to hold a operating gun in position ,depends on the mass of it?
consider the following example - there are two persons A and B.A is having a 10 kg gun and B is having a 5 kg gun. Both guns are shooting the same type and number of bullets per second. Now ,which of the two persons would require to exert a greater force to hold the gun in position?
If the force require to hold both the guns in position is the same(which I think it is ),then is it not counterintuitive?? I mean ,imagine to exert the same force to the 50 kg gun and a 5 kg gun, to hold them in position??
 ANSWER:
ANSWER:
This problem is a little trickier than I expected. Here is
the way I approached the problem: imagine that there is nothing holding
a gun of mass M shooting a bullet of mass m. Then you can
use momentum conservation to find the relative speeds of the bullet, v, and the gun,
V, after being given an amount of energy
(from the gunpowder in the bullet) E; V=(m/M)v.
Usually, M>>m, so v>>V, so it might seem
that the lighter gun would go faster and be harder to stop; but the
catch is that it is easier to stop something with less mass, so it is
not really clear which is easiest to stop until we can write what the
speed V is. You might think I have already done that, but the
speed of the bullet v depends on the mass of the gun. To get rid
of v in my equation for V you need to introduce the
constant energy which gets given to the gun and the bullet, E=½mv2+½MV2.
If you now solve this equation for v, substitute that into the
equation for V, you find V=√[(m/M)(2E/(m+M))].
Now, in order to stop this motion in a short time Δt you must
exert a force F=MV/Δt=√[(2mME/(m+M))]/Δt.
If you examine this, you will see that if M>>m, as is almost
always the case, F≈√[2mE]/Δt, independent of
M.
For smaller gun masses where the bullet and gun have comparable masses,
I have plotted the force (divided by the constant √[2mE])
as a function of M/m. This is shown in the graph to the
right and you can see that it is easier to stop a lighter gun
.
For the usual case where the gun is much
more massive than the bullet, it is easy to see intuitively that force
is independent of mass. In that case, the velocity of the bullet will be
essentially the same for each case so v is not (to an excellent
approximation) a function of M. So, V is inversely
proportional to M and, since F is proportional to MV,
F must be independent of M.
 NOTES
ADDED:
NOTES
ADDED:
It occurred to me that one could also define "recoil" as the
force necessary to stop the gun in a given distance
Δx
(rather than in a given time
Δt
as above). Then the
magnitude of the work done by that force must be equal to the kinetic
energy the gun had, FΔx=½MV2=½M(m/M)(2E/(m+M))=E/(1+(M/m)).
In this case, it is clearly easier to stop a heavier gun.
So, how recoil is defined is important in
discussing this question. A little research reveals that, indeed, gun
enthusiasts do not think of perception of recoil as what they mean by
recoil. Rather, there are several types of recoil which are used to
quantify the effect. Recoil velocity is what I have called V;
recoil energy is ½MV2; recoil momentum
is MV; recoil impulse is the time it takes the gun to
accelerate from rest to V, essentially the time the bullet is in
the barrel (not what I call Δt). This is eminently sensible
since each of these is unambiguously defined. Perception is rightly
considered to be qualitative, dependent on the person firing the gun.
I also should note that my analyses above
assume that perception begins when V has been acquired, but this
is not really what happens because you actually start feeling the recoil
at the instant the gun is fired. So you can ask what force you need to
exert during the time the bullet is accelerating to hold the gun at
rest; so, when the bullet exits the barrel, you experience no more
force. Clearly this force is independent of M since the gun never moved.
Now all bullets to which a constant energy E has been added exit
with a velocity v=√(2E/m) because by holding the
gun still you effectively make its mass infinite. Approximating that the
acceleration, and therefore the force, is constant while the bullet is
in the barrel, it is pretty easy to show that F=E/L where
L is the length of the barrel. Again, there is no dependence on M.
Of the three kinds of "recoil perception" I have defined, I think this
last one makes the most sense.
 QUESTION:
QUESTION:
Let's say that I have mallet attached to a rotating axle, in such a way that the mallet is perpendicular to the axle, and the base of the mallet's handle is attached to the axle.
Let's also say that the mass of the mallet is known (the entire mallet, not just the head), and the speed at which the mallet head is traveling is known.
With that in mind, how do I calculate the kinetic energy involved if this silly rotating mallet contraption were to strike something with the mallet head?
I'm aware that the equation for kinetic energy is normally k=(1/2)mv^2, but I don't know if that equation would apply in this situation.
In short, I seek an equation to calculate the kinetic energy involved in this situation.
 ANSWER:
ANSWER:
The kinetic energy K of your rotating mallet is
not ½mv2,
because the speed the whole mass m is not v. The velocity
which is important is the angular velocity, ω, which is
the number of radians per second the object is rotating; since there are
2π radians in a full circle, ω is related to the frequency
f, the number of revolutions per second, by ω=2πf.
Then the velocity of any point on a rigid body which is a distance
r
from the axis of rotation is v=rω. So, an atom, say, near the
axis of rotation contributes less to the kinetic energy than one far
from the axis. So your mallet's kinetic energy depends on the geometry
and how the mass is distributed over that geometry. This is taken care
of by introducing what is called the moment of inertia, I,
which plays the role in rotational physics that mass plays in
translational (in-a-straight-line) physics, such that kinetic energy may
be written as ½Iω2. I can give you an approximate
moment of inertia for your mallet. If the size of the head is much
smaller than the handle is long and the length of the handle is much
larger than its thickness, you can approximate the head as a point mass
and the handle as a thin stick. I will call the mass of the handle m,
the length of the handle L, and the mass of the head M. In
that case, I=[M+(m/3)]L2. So, the
energy would be K≈½[M+(m/3)]v2
where v is the speed of the head.
 QUESTION:
QUESTION:
I am 15 years old and want to become a physicist, and I have a question about Sir Isaac Newton in relation to gravity and the moon. Newton asked the question "If the apple falls, does the moon also fall?" He then proved that the moon indeed falls, and is constantly falling around the Earth. But since every free-falling object falls at approximately the rate of 10 meters per second squared, then why does the moon orbit the Earth at a constant speed?
 ANSWER:
ANSWER:
Acceleration is the rate of change of velocity but velocity
can change in two ways, either by changing its magnitude (speed) which
is what you are thinking of, or by changing its direction. An object
moving with constant speed v in a circle of radius R has
an acceleration of v2/R.
 QUESTION:
QUESTION:
My Question is, if you were in a spaceship in space with no windows, what experiment could you perform in order to prove whether you were moving or not moving?
 ANSWER:
ANSWER:
There would be no such experiment, because "moving" only has meaning only relative to
something else. If you were not burning your engines (that is there were
no forces acting on your ship), Newton's laws of motion would be correct
laws of physics in your ship. However if you were burning your engines
but you did not know that for sure, there would be no experiment you
could perform to determine whether you were accelerating or whether you
were in a gravitational field.
 QUESTION:
QUESTION:
We know that space and time are not absolute in our universe. My
question is: what causes space and time to be relative in our particular
universe? In a multiverse scenario can we think of a universe where
space and time may not be relative?
 ANSWER:
ANSWER:
The reason that time and space are not independent is that
there is something in our universe (light) which, no matter who measures
its speed the same value is found. Since speed is the ratio of a length
(space) to a time, there is no way this could be true in a universe
where time and space were not linked. I do not speculate about
multiuniverse scenarios!
 QUESTION:
QUESTION:
A planet was discovered, Gliese 581g, that is 20 light years from Earth. This planet is the right size and distance from its' sun to have liquid water on the surface and therefore life. How long would it take to reach this planet traveling at 18,000 mph, the approximate speed at which our rockets can can currently travel?
 ANSWER:
ANSWER:
20 ly is about 1.2x1014 mi, so t=1.2x1014/1.8x104=6.7x109
hr=760,000 yr.
 QUESTION:
QUESTION:
Is there known upper limit of the acceleration? and if it exists, what is its formula as a function of physics basic constants?
 ANSWER:
ANSWER:
Acceleration is change in velocity over elapsed time,
a=Δv/Δt.
There is an upper limit on how much velocity can change, since the
velocity of any object with mass must be less than the speed of light c, Δv<3x108 m/s. There is, however, no known limit
to how small Δt can be, so there is no limit to how large a
can be. It has been suggested that perhaps there is a minimum time
interval called the Planck time which is about 3.4x10-44 s,
so the maximum possible acceleration would be about 1052 m/s2.
 QUESTION:
QUESTION:
How is the weight of a planet (e.g. Earth's) measured?
 ANSWER:
ANSWER:
The mass of anything can be determined if you know its
gravitational field. For example, to find the mass of the earth you can
measure the acceleration due to gravity which is about 9.8 m/s2. Then,
if you know the universal law of gravitation, the acceleration a
of an object a distance R from the center of the planet is a=MG/R2 where
G=6.67x10-11 m3/s2/kg
and M is the mass of the earth. The radius of the earth is about
6.4x106 m, so M=9.8x(6.4x106
)2/6.67x10-11
kg=6x1024 kg. [I note that you ask about the weight of
the earth. By definition, the weight of something is the force the earth
exerts on it, so you should ask how the mass of a planet is measured.]
 QUESTION::
QUESTION::
Newtons Law states that to every action there is an opposite and equal reaction. If a cue ball is stuck hard enough and strikes another ball, the other ball moves off with the same speed at which it is struck, while the cue ball stops dead. This is providing the cue and cue ball and struck ball are in a dead straight line. Does this mean that the cue ball has transfered all of its energy to the ball that moves off therefore not being able to follow on?
Have just found your site and find it very interesting and so give to you my thanks.

 ANSWER:
ANSWER:
This is an "action/reaction" example (Newton's third law)
only in an indirect sense: because the balls, when colliding, exert
equal and opposite forces on each other, their total momentum must not
change (be conserved). Billiard balls are very elastic and therefore, to
a good approximation, energy is conserved also. For the one-dimensional
case where one ball is initially at rest which you cite ("dead straight
line"), there are two equations to solve:
-
momentum
conservation, m1v1=m1u1+m2u2,
and
-
energy conservation,
½m1v12=½m1u12+½m2u22,
you take longer to
where m1 is the mass of the
incoming ball, m2 is the mass of the other (at rest) ball,
v1 is the incoming speed, and u1 and
u2 are the outgoing speeds. If you solve these, you get the
speeds after the collision:
-
u1=v1(m1-m2)/(m1+m2)
-
u2=2m1v1/(m1+m2).
So, if m1=m2
(as for billiard balls), u1=0, u2=v1,
as you note. And, certainly, as you also note, the first ball has
transferred all its energy (and momentum) to the second ball. Since I have
gone to the trouble of solving the problem generally, we might as well look
at a couple of other special cases. Suppose that m1<<m2;
this would be like colliding your cue ball with a granite wall. In that case
u1≈-v1 and u2≈0, where
≈ means approximately equal; this is just what you would expect, the ball
bounces back (that is what the - sign means) with the speed it went in and
the wall stands still. Similarly suppose that m2<<m1;
this would be like colliding your cue ball with a BB. In that case u1≈
v1 and u2≈2v1; so the cue
ball never knew anything happened and the BB ends up going twice as fast as
the cue ball.
Incidentally, for completeness, there is a second
solution when you solve the two conservation equations, sometimes referred
to as the "trivial" solution. You should expect two solutions because one of
the equations is quadratic. The second solution is
-
u1=v1
-
u2=0.
This is called trivial because it would correspond
to missing totally and you would certainly expect the energy and momentum to
be conserved if the collision never happened.
 QUESTION:
QUESTION:
would it be possible to have a particle accelerator as an engine for a spaceship? Where by rerouting particles that are moving near the speed of light and making them collide with the back of the spacecraft would give the spacecraft a push in the back?
 ANSWER:
ANSWER:
You are essentially asking "if I, standing in my spaceship,
push on the front wall, will it go faster?" Whatever impulse you gain by
pushing forward with your hands will be cancelled by the frictional
force your feet exert backwards. Similarly, the impulse you get from the
push from the particles forward would be negated by the force necessary
to "reroute" them or to accelerate them in the first place. Anything you
do inside a closed system cannot change the momentum of that system. If
you were to fire the particles out the back like a rocket you could
propel the spaceship; this is the idea of
ion-drive
thrusters.
 QUESTION:
QUESTION:
if we see an object because of light from the source hitting the surface of the object make its electrons to excite to higher orbits and comming back to same orbit emiting a photon which strikes our eyes, then according to this, at one INSTANT of TIME, an excited electron can emit only one photon and similarly if the object contained (for example) ten electrons on its surface, only ten photons can come form that object at that instant of time and all those photons will have 3 degree of freedom to move in any direction.IF this is the case, we coudnt see a complete object at a given instant of time as all the photons emitted from that object woudnt have striken to our eyes and similarly, if 3 people are watching the same object, at a given instant of time, each person would have seen a part of that object as one electron emitts only one photon at that instant of time.... but this is not the case in real world....how is it?
 ANSWER:
ANSWER:
First, there will never be a situation where there are ten participating
electrons on the surface, more like 1020 electrons/m2.
You are correct that the light emitted by any single atom can be in any
direction―that is why everybody who is looking at an object can see it.
But the situation you describe would be for extremely low intensity
light illuminating the object you were looking at. Suppose the light
striking the object had an intensity of 10 photons/s/m2; in
that situation, you might have to wait a few minutes to see a photon
from some particular point on the object and you would only see a little
flash of light. So, you would not be able to "see" the object because
seeing means that your brain sums the effects of many photons in a short
time. However, if you put a camera where your eye was and leave the
shutter open for several hours, you would "see" the object.
 QUESTION:
QUESTION:
if a radioactive atom ejected a high speed (beta particle)from its nuclues, would the remainder of the nucleus recoil with the same speed?
 ANSWER:
ANSWER:
The total energy and total momentum of the system must remain
constant. If the nucleus before decay is at rest, then it has zero
momentum. After the decay, the β particle and nucleus must move
in opposite directions to conserve momentum. If you think of momentum as
mv, the nucleus, having a much larger mass, must have a much
smaller speed to have the same magnitude of momentum as the β
particle. To really do this quantitatively, you would not use mv
as the momentum since the β particle is a relativistic particle
(moves at a speed not small compared to the speed of light), and there
is a third particle (a neutrino) which also carries energy and momentum;
but a classical argument like mine above gets at the crux of the matter
that the lighter particle must move faster.
 QUESTION:
QUESTION:
For my Science Fair project about balloon-powered Hover craft, I did an experiment to find whether air volume in a balloon (using different sized balloons) is proportional to the hover time of the hover craft. I found out that larger the air volume of the balloon, longer is the hover time. But it is not proportional. On an average, a 5" balloon hovered for 31.9 seconds, a 9" balloon took 2 min and 45.3 sec and a 12" balloon stayed for 4 min 17.5 sec. If it were directly proportional, 9" balloon should have taken 57.42 sec and 12" should have taken 1 min. 27.6 seconds. Why is the hover time not proportional to the air volume, in spite of keeping all other variables constant? Please help me understand.
 ANSWER:
ANSWER:
You make a common mistake―the volume of a sphere is not
proportional to its radius, it is proportional to its radius cubed.
Therefore, if you plot time as a function of the cube of whatever 5, 9,
and 12 measure (diameter, radius, it really doesn't matter), you are
finding how the time depends on the volume which you know is what should
matter. Or you may want to be very fancy and plot time as a function of
volume, volume being 4πR3/3 where R is the
radius of the balloon.
 QUESTION:
QUESTION:
My figures are not exact, just my estimate.
The circ. of the earth is close to 25,000 miles at the equator.
From pole to pole it is less. I read that this is due to the earths rotation of about 1000 mph. at a radius of 12,500 miles.
I believe that this is due to centrifugal force caused by the rotation at that distance..
Does that mean that a person would weigh less at the poles then at the equator due to centrifugal force? Also if the earth would stop rotating, would a persons weight increase at the equator?
 ANSWER:
ANSWER:
First, I have to give my stock response that the weight is
the gravitational force exerted on something and that has nothing at all
to do with rotation. What you really want to know is what is apparent
weight, the weight you would read with a scale you were standing on.
Think about it for a minute: if the earth spun faster and faster,
eventually the gravity would not be able to keep you from going off the
surface. So the centrifugal
force would cause your apparent weight to be smaller at the equator
than at the poles. It is a very small effect, though, only about 0.3%.
 QUESTION:
QUESTION:
Do objects colder than a person would normally experience radiate its thermal energy in frequencies longer than Infrared (ie Radio)? I know that as temperature increases an object will radiate in shorter frequencies, and it seems that initial radiation in Infrared would be arbitrary. If I have the wrong idea and the majority of radiation up to a certain temperature would be in Infrared I would be interested to find out why.
 ANSWER:
ANSWER:
All objects radiate at all frequencies. The most intense
frequency does, indeed, increase with temperature and the colder an
object is, the longer the wavelength of its most intense radiation is.
Also, the total amount of radiation varies like T4, so
if you want to look for radio frequencies there might be more at a
higher temperature even though it was not the biggest.
 QUESTION:
QUESTION:
I understand why we use magnetism to smash particles against each other to find out what they are made from. Yet I don't understand why we don't find a way to use the strong force to bring those sub light speed particles up to and over the speed of light.You know like when the starship Enterprise goes back in time using gravity assit? At the last billionth of a second we might be able to suspend a stripped down atom to get to its strong force and it it again with colliding protons that would bend slightly by the strong force to jump the particles closer to the speed of light? So why not?
 ANSWER:
ANSWER:
The issue is not how strong the force is, rather how much
energy can it deliver. For an object to exceed the speed of light, an infinite amount of energy is required.
No finite force can do that in a finite amount of time.
 QUESTION:
QUESTION:
I have recently learnt about torque, but i have a confusion regarding its concept: Suppose you have two identical doors with the only difference that the hinges of one are well lubricated and the other's hinges are worn out, and cause more friction than the first one. To open the doors at the same speed, it is clear that i have to apply a greater force on the second one. As torque is the product of of force and perpendicular distance, the numerical value of the torque in the second door comes out to be greater. But in the sense that torque is that how much a body turns, both of them have the same torque. Which of the two ways is correct?
 ANSWER:
ANSWER:
You have to include all the torques on the door, not just the
one you apply. For both doors there is a torque due to friction of the
hinges, the second one being larger. Since the frictional torque acts
opposite your torque (it tends to slow the door down, while yours tends
to speed it up), it should be subtracted from your torque. So, to open
the doors at the same rate, your torque on the second door must be
larger.

 QUESTION:
QUESTION:
Is it true that a Wave Train travels at 1/2 the speed of its constituent waves? If so, why? I mean, say a storm in the Gulf of Alaska stirs up some seas. We might see, some distance away, that individual swell waves are moving at 30 knots, but from a bird's eye view, we would see that the area of disturbance expands toward Hawaii at only 15 knots. If this is true, is it only true of transverse waves. Is there such a thing as a longitudinal wave train?
 ANSWER:
ANSWER:
What you are talking about is that wave packets or wave
trains are composed of more than one wavelength and there is dispersion,
i.e. different wavelengths travel with different velocities in
the medium; this is known as dispersion and is the reason that a prism
breaks white light into a spectrum of colors. There are, as you note,
two kinds of velocity. The velocity of the waves themselves is called
the phase velocity and the velocity of the wave packets is called group
velocity. For water waves the result is that the group velocity is half
the phase velocity. I did not know this; it is apparently true for water
surface waves in deep water. The little animation above is for just this
situation; the green dots travel with the packets (group velocity) and
the red dots travel twice as fast with the waves (phase velocity).
Everything I have said applies just as well to longitudinal waves.
 QUESTION:
QUESTION:
 We've learned recently about the strong and weak nuclear forces. We also learned that when an isotope has too few neutrons, the nucleus stabilizes itself by having an electron from one of its orbitals crash down into a proton and turn it into a neutron. What I don't understand is
how does the nucleus as a whole know it is not stable, if it just an inanimate collection of matter? In other words, how does a proton know it needs to turn into a neutron, how does it know that there isn't that extra neutron on the other side of the structure, how does it know that it needs to sacrifice if it is inanimate, if it can't see or talk or anything? And furthermore, when this happens, how do the electrons know they have to crash into the nucleus? How do they know where to go, and where do they get the momentum to do this? Who pushes them? And to further my question, who's to say that an isotope with two few neutrons doesn't have all of its protons simultaneously trying to stabilize, causing the whole structure to be a bundle of neutrons?
We've learned recently about the strong and weak nuclear forces. We also learned that when an isotope has too few neutrons, the nucleus stabilizes itself by having an electron from one of its orbitals crash down into a proton and turn it into a neutron. What I don't understand is
how does the nucleus as a whole know it is not stable, if it just an inanimate collection of matter? In other words, how does a proton know it needs to turn into a neutron, how does it know that there isn't that extra neutron on the other side of the structure, how does it know that it needs to sacrifice if it is inanimate, if it can't see or talk or anything? And furthermore, when this happens, how do the electrons know they have to crash into the nucleus? How do they know where to go, and where do they get the momentum to do this? Who pushes them? And to further my question, who's to say that an isotope with two few neutrons doesn't have all of its protons simultaneously trying to stabilize, causing the whole structure to be a bundle of neutrons?
 ANSWER:
ANSWER:
This is not exactly a single, well-focused question as
stipulated by the the groundrules of this site, but I will answer some
of your questions with a general description of beta decay which is what
you are talking about. In some sense, that inanimate collection of
matter as you call it, does know what to do because it is a quantum
mechanical system subject to rules. The most important rule, perhaps, is
that a nucleus will seek the lowest energy state. Consider a nucleus
which has an atomic weight A, composed of N neutrons and
Z protons such that N+Z=A. Nuclei of a given A are
called isobars. So, N could be anything from 0 to A with
Z=A-N. In practice, nuclei which are bound at all must have both
protons and neutrons. Take a specific example: Plotted to the right is
the binding energy of the known isobars of A=73 plotted as a
function of Z. Binding energy is essentially the energy you would
have to supply to totally disassemble a nucleus and the more tightly
bound a nucleus is, the lower the energy state. So, if nature provides a
way to keep A constant but change Z and N, a
nucleus will take advantage of it. So, Zn and Ga have too few protons
(or too many neutrons, however you choose to look at it), and they will
decay by turning a neutron into a proton plus an electron plus a third
particle called a neutrino (which has practically no mass and no
charge). Because the energy of the nucleus decreases, the leftover
energy is used to shoot out the electron and neutrino. This is called β-
decay. But, when these two get down to Ge they will go no farther
because energy would have to be added to get to As and there would be
none left for the electron and neutrino. On the other side, As and Se
have too many protons (too few neutrons) compared to Ge and so they have
to hope that nature provides a way to turn protons into neutrons.
Indeed, a proton can decay into a neutron plus a positron (a positively
charged electron) plus a neutrino. This is called β+ decay.
Finally, there is a process which can compete with β+ decay
which is called electron capture which is what you refer to in your
question. There is a swarm of electrons around the nucleus and if a
proton could combine with one of them it would do so. Indeed, this is
allowed if a neutrino is ejected. The electrons do not have to suddenly
"crash into the nucleus", they are already there. The electrons in an
atom do not really run around in little circular orbits, they are
smeared everywhere, even inside the nucleus; there is a small but
nonzero probability of looking for an electron inside the nucleus and
finding it there. I think if you read through my answer carefully you
will find I answered all your questions. Nature is "smarter" than you
give her credit for!
 QUESTION:
QUESTION:
how can the laws of relativity relate to quantum physics...since these are the only laws we know of , doesnt that invalidate using them for quantum physics, since quantum mechanics is so very different than the world we exist in?
 ANSWER:
ANSWER:
Relativity is certainly applicable on the quantum level. In
fact, that is where we get most of the hard evidence to support the
theory of special relativity because only for very small objects is it
practical to achieve velocities comparable to the speed of light.
Nuclear physics provides the most convincing evidence for E=mc2
as evidenced by nuclear power and weaponry. The usual formalism of
quantum mechanics (e.g. Schrödinger's equation) is not a
relativistic theory in itself, but relativistic corrections can be made
to calculations. There is a theory of quantum mechanics which is
relativistically correct version of quantum mechanics (using either the
Dirac equation for fermions or the Klein-Gordan equation for bosons).
So, there is no incompatibility between quantum mechanics and
relativity.
 QUESTION:
QUESTION:
What happens when two magnetic fields collide. Both positive into positive (or negative to negative) and positive to negative.
 ANSWER:
ANSWER:
What does that mean, "collide"? If you have two sources of
magnetic field and at some point in space the field from one is B1
and from the other is B2, the net field at that
point is simply the vector sum of the two, B=B1+B2
.
For example, if B2=-B2
at some point, the field there would be zero.
 QUESTION:
QUESTION:
Hey, so muons falling down towards the Earths surface survive decaying before they reach the surface because of length contraction as a result of Special Relativity. But I read SR doesn't apply when the object is accelerating. Aren't the muons accelerating due to Earths gravity? What have I understood wrong?
 ANSWER:
ANSWER:
First of all, special relativity can be applied to
accelerating objects. Acceleration does not play a central role like it
does in Galilean relativity because it is not invariant; what this means
is that if two observers in two different inertial frames measure the
acceleration of some object, they get the same answer in Galilean
relativity but different answers in special relativity. Nevertheless, at
any instant the object (muon in your case) has some velocity and special
relativity may be applied at that instant. But, while that is important
to understand, it is essentially irrelevant in the case of muons
approaching the earth. A muon lives on the order of 10-6 s
and has a relativistic speed, say 2x108 m/s; with an
acceleration of about 10 m/s2, its velocity changes by about
10-5 m/s over its lifetime. Hardly accelerating, is it?

 QUESTION:
QUESTION:
I'm looking for a generator to produce 100% of my current electrical usage and my usage rate is 1,400 kw/h im seeking to find what volt generator i need to buy . would a 50 kw generator be too much or to little?
 ANSWER:
ANSWER:
Well, you have your units of electricity muddled, so let's
get that straight first. A watt (W) is a measure of the rate you
use energy, one joule (J) of energy per second. For example, a 1000 W
dryer uses 1000 J per second or 1 kW. The most common measure of energy
used is not the joule but the kilowatt hour (kW·h), not kW/h as you
write. When you say your "usage rate
is 1,400 kw/h", you
must mean that you use 1400 kW·h per month. Now, there are 24x30=720
hours per month, so your average power consumption is 1400 kW·h/720 h,
about 2 kW. So, a 50 kW generator is probably overkill. On the other
hand, probably at least half of every day you use next to nothing, so a
better average is probably like 5 kW, still 10 times less than 50 kW.
But, what you really need to think about is your peak usage.
Energy hogs are typically anything which creates heat by getting a coil
hot--clothes dryers, electric ovens and stove tops, toasters, water
heaters, etc.--which are typically 1-3 kW each. Air conditioners
also use a lot of power, often 3-4 kW, so your usage is probably
seasonal. All things considered, something in the range of 10-20 kW
should do it.
 QUESTION:
QUESTION:
if you could release ALL the energy in matter, that holding the quarks together, etc, completely, can you give me an example in ballpark terms as to what it would be like. for example if you released all the energy of a gram (or even a single molecule if it would be recognizable) of some heavy element, what would you see?
 ANSWER:
ANSWER:
This is pretty straightforward and does not depend on what
that gram is made of. E=mc2=10-3 kg (3x108
m/s)2≈1014
J. The bomb dropped on Nagasaki in WWII had an energy of about 1014
J.
 QUESTION:
QUESTION:
how many thermonuclear bombs would you have to explode per sec to much the solar energy intersepted by the earth every sec.
 ANSWER:
ANSWER:
A typical H-bomb is about one megaton of TNT which is about
4x1015 J. The solar power striking the earth is about 170x1015
J/s. So you would need about 40 bombs per second.
 QUESTION:
QUESTION:
We've been learning about nuclear decay and radiation lately in AP Chemistry( I am junior in high school), and this question crossed my mind:
If protons can absorb electrons, what if a neutron absorbed a positron? I was imagining that if we had a neutron emitter pointed to the same place a positron emitter was pointed, positrons might merge into some neutrons and create protons. Then i wondered, now what if we were to isolate this new proton into a separate chamber of this weird apparatus I cannot fully explain, in which we emitted electrons, and thus making the proton into a neutron again, except it is now one electron and one positron heavier. Now what if we continued this cycle? Would the neutron become unstable as do heavy elements? Are current-day neutrons nothing but the development of the said process to the most stable form, as the amount of positrons and electrons must be just right? If we managed to force more positrons and electrons into the neutron than naturally allowed, would it be like nuclear fission, but make an explosion that is thousands of times greater than a hydrogen(fusion) bomb? Or will there be such a tiny mass defect when the neutron gets too large that it only explodes the apparatus and nothing more?
 ANSWER:
ANSWER:
Here is the thing to appreciate first off: a neutron is a
neutron is a neutron. There is no such thing as a heavier or lighter
neutron, its mass must be equal to the known neutron mass. Likewise for
protons or any other elementary particle. So, most of your question
has no answer because the basic premise is wrong, but I will tell you a bit about
these processes (generally called beta decay or weak interaction
processes). No matter how you choose to create any elementary particle,
the energies (including the mc2 energies of the
particles) of all the participating particles before and after the
creation must be exactly the same. Electron (e-) capture by a proton is a common
nuclear decay mode, resulting in a neutron (n) afterwards.
Similarly, positron (e+) capture by a neutron is possible (but rare) and results in a
proton (p)
afterwards. One thing you miss, though, is that there is a third
participant, a neutrino (ν), which exits afterwards in both cases. The
reason that electron capture is common is that the nucleus is surrounded
by a cloud of electrons available for capture; positrons are not
normally around unless you put them there and then they are much more
likely to annihilate with one of the many electrons before getting the
chance to interact with a neutron in the nucleus. So, let's talk about
the energetics of these reactions:
-
Rather than using
masses in kg, I will use rest mass energies Mc2 in MeV
(million electron volts). [I assume that, since you are in an AP course
and talking about nuclear chemistry, you are familiar with the electron
volt as a measure of energy; if not, it is the energy an electron
acquires when accelerated across a potential difference of 1 volt.] The relevant masses are:
Mnc2=939.565378, Mpc2=938.272046,
and Me-c2=Me+c2=0.510999.
The neutrino has approximately zero mass. Although these are energies,
it is customary, if a bit sloppy, to refer to these numbers as masses
which I will do.
-
We will also need
sums of masses, Mpc2+Me-c2=938.783045
and Mnc2+Me+c2=940.076377.
-
For electron
capture, p+e-―> n+ν. Note that the sum of the mass on
the left is 938.783045 and on the right is 939.565378. That means that
if all masses are at rest before and after the capture, this is
impossible because there is not enough energy before to create a
neutron. The way this can happen is if the electron brings at least
0.782333 MeV of kinetic energy with it when it encounters the proton and
then any leftover energy will be shared by the kinetic energies of the
neutron and the neutrino. The energetics also tell us that the neutron
is not a stable particle because its mass is greater than the masses of
the particles it could decay to and a free neutron will decay, n―> p+e-+ν.
The half life of a free neutron is about 15 min. In a stable nucleus a
neutron does not decay.
-
For positron
capture, n+e+―> p+ν. Note that the sum of the mass on
the left is 940.076377 and on the right is 938.272046. There is adequate
mass to create the new mass and the excess energy is carried off by
the neutrino. It also tells you that the free proton is a stable particle
(at least against decaying into a neutron and positron) because where
would the extra energy come from?
So, a proton
(neutron) does not get a little heavier each time it combines with an
electron (positron) and then with a positron (electron), you end up with the
mass of the proton (neutron) again.
 QUESTION:
QUESTION:
The concept of teamwork can be illustrated by the two-horse rule. If one horse can pull 700 pounds and another horse can pull 800 pounds, how much weight will they pull yoked together? The answer may surprise you. The two-horse team will pull their own weight plus the weight of their interaction. Therefore, yoked together, the horses can pull 3000 pounds!
My coworkers and I were wondering if something like this was true, could two horses pull more than the sum of their individual maximum pulls, and if so why?
 ANSWER:
ANSWER:
This is perhaps the goofiest thing I have heard recently.
When you say that a horse can pull 700 lb, you are specifying the
maximum force he can exert in a horizontal direction, not how much
weight he can pull forward. If that horse could just drag a 700 lb box
sitting on the ground forward, he could probably be able to pull 7000 lb
if mounted on wheels. The weight of a horse is a force which is
vertically downward and any horizontal force would have no effect on
that force. Those two horses could exert a maximum force of 1500 lb.
 QUESTION:
QUESTION:
I was reading Brian Greene's The Fabric Of The Cosmos and I was wondering if you could explain something to me. Einstein holds that Gravity
& Acceleration are equal to one another. So Let's say I throw myself off a very tall building and experience the gravitational pull downward. Einstein would say that I am accelerating upward. Can you please explain to me how this is possible? Does Gravity
& Acceleration zero one another out. In other words do they cancel each other? is this why they remain equal?I
 ANSWER:
ANSWER:
It is not quite right to say that "gravity and acceleration
are equal to one another". So, let's review the equivalence principle
which says that, if you are in a box with no windows, there is no
experiment which can be performed which can distinguish whether you are
in a gravitational field with gravitational acceleration g or
that your box is in empty space and has an acceleration g.
Einstein would not say that if you are accelerating down in a
gravitational field that you were accelerating upward; he would say that
there would be no experiment you could perform which could distinguish
your current state (accelerating down in a gravitational field) from not
accelerating at all in the absense of a gravitational field. An amusing
anecdote (perhaps not true): Einstein, employed as a patent clerk in
Switzerland, was able to discharge his duties quickly and spend the rest
of the day daydreaming about physics, supposedly the environment which
allowed his brilliant discoveries in 1905. One day when he was
daydreaming and watching a housepainter across the square he witnessed
the painter fall from his ladder and had a eureka moment vis a vis
the equivalence principle.
 QUESTION:
QUESTION:
I was delivering a 5FT by 4FT glass picture frame. It was in my empty box truck, strapped up against the wall. I use standed tie down straps to secure the frame. May I note, that the front of the frame where the glass was covered with a cardbroad that covered the dimensions of the picture frame. I live in New York City where there are many potholes. While transporting the picture frame i heard a loud pop, then a few moments later I heard glass breaking. I would like to know if there was something i could have done to prevent this from happening or are there other forces involved?
 ANSWER:
ANSWER:
What causes glass to break? You have to exert a force on it.
When standing vertically, the only force is the force of the floor up on
the glass which is equal to the weight of the glass, and the force of
the straps on the glass which should be pretty small because if you are
going straight at constant speed, the glass does not want to fall over.
Apparently the force from the floor is not enough to break the
glass because if you are standing still or going with constant speed it
does not break. But suppose you hit a bump. Suddenly, in a very short
time, the horizontal velocity of the glass changes because the truck and
the glass are both suddenly going upwards. A change in velocity means an
acceleration and if the change in velocity is Δv in the vertical
direction and that happens in a time mattΔt, the acceleration a
in the vertical direction is a=Δv/Δt. So, what
causes an acceleration? Newton's second law tells us that if an object
of mass m experiences an acceleration a, there must be
some unbalanced force F=ma on the object. In your case, the floor
suddenly has to push upwards with a force bigger than the weight of the
glass. That is the force which breaks your glass. So you need to figure
out how to reduce that force. Now, the shock absorbers of a vehicle are
supposed to minimize the effect of bumps. But trucks often have quite
stiff suspension systems and are not as smooth a ride as a luxury sedan.
So you need to put a special shock absorber for your glass. The way you
reduce a for a given Δv
is to make Δt bigger, that is make the time of speeding up (or
slowing down) longer. If you put a piece of foam rubber under the glass
it will make the time longer and the force smaller. However, be sure the
straps are not too tight or else the glass will not be able to move with
a different vertical speed during the bump than the truck. Incidentally
the same thing happens when you are slowing down. If you fall from 20'
up onto concrete you get badly hurt because you stop very quickly; but
if you fall on a big thick matress, your pain will be much less because
you take longer to
stop.
 QUESTION:
QUESTION:
.5*mass*V2= KE but what do you do with kinetic energy? how would i turn that number in to say ft/lbs or PSI?
 ANSWER:
ANSWER:
You are asking me, I guess, how to convert units. I always
recommend a nice little piece of free software called
CONVERT. You
evidently want to convert in English units, so the mass and velocity in
½mv2 would be slugs and ft/s, respectively. A slug is
a mass whose weight is 32 lb; the mass of an object which weighs
W lb is m=W/32 lb·s2/ft. For example, suppose
you have a 10 lb weight which has a speed of 5 m/s. Then KE=½·x10x52
(lb·s2/ft)·(ft/s)2=125 ft·lb. So, you see
that you should have asked me what the kinetic energy was in ft·lb, not
ft/lb. Energy (and torque and work) is measured in ft·lb in English
units. PSI, lb/in2, is not a measure of energy, it is a
measure of pressure. [I know this is tedious, but it shows you why
scientists prefer to work in SI (metric) units because the kilogram is
the unit of mass and the above calulations would not have required that
I convert slugs into units like lb·s2/ft. If I had said that
I had a 10 kg mass with a speed of 5 m/s, its energy would have been 125
kg·m2/s2=125 J where J is the Joule, the unit of
energy in SI units. A Joule is also a Watt·second.]
 QUESTION:
QUESTION:
in the formula for HP (HP=TQ*RPM/5252) do you know where the constant 5252 comes from and what it represents?
 ANSWER:
ANSWER:
Horsepower is a measure of power, energy per unit time. The
units of torque (I assume TQ is torque) are force times distance
(e.g. ft�lb or N·m) which are also the units of energy and
RPM
is revolutions/minute, which has the dimensions of 1/time, so your
formula for horsepower indeed has the units of power, essentially
energy/time. The trick is how to get it into the proper units. I am
guessing that torque is to be measured in ft·lb. Now, 1 hp=550 ft·lb/s
and TQ*RPM=ft·lb·rev·min-1·(2π/1 rev)·(1
min/60 s)=0.10472 ft·lb/s, so P=TQ*RPM/(550/0.10472)=TQ*RPM/5252.1
where P is power in hp, TQ is torque in ft·lb, and
RPM
is angular velocity in rev/min. So my guess that TQ is in ft·lb
was right. So what the 5252 "represents" is what you must divide by to
get the wrong units (ft·lb·rev/min) into the right units (hp). [The
purpose of the (2π/rev) factor is that there are 2π
radians in one revolution.]
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
So if i'm understanding it right HP shows energy over time. What i was trying to understand is why HP matters. In my experiance with cars at the race track given as close to identical as posable cars, the one with more HP wins. Sometimes even if the other car had a signifigant torque advantage. With what you said this makes sense because in a given amount of time the car with more HP is inputting more energy in to the driveline than the car with less hp.
Or did i not understand that at all?
 ANSWER:
ANSWER:
You have it exactly right. What matters is the rate at which
energy is delivered to the car. You might also be interested in an
earlier answer in
which the power is part of the answer.
 QUESTION:
QUESTION:
if im traveling 40 mph on a scooter and the temp. is 32 degrees what will the temp feel like with the wind chill facter
 ANSWER:
ANSWER:
The chart to the left gives selected values of speed and
temperature. Also given is the equation used to calculate it. In your
case, Wind Chill=15.80F. You might look also at an
earlier answer for more
detail.
 QUESTION:
QUESTION:
If someone sent a telegraph in say, 1862, could it radiate outward to the universe.
 ANSWER:
ANSWER:
Sure, but its intensity would be so low that you could never decode it or probably even recognize it as made by an intelligent being. Since the message in 1862 would have been over a wire and not by radio (the first wireless telegraphy was in 1899), the radiated signals would be extraordinarily weak.
 QUESTION:
QUESTION:
I am really facing great difficulty in understanding Planck's Theory.What is meant by energy being 'continuous' or being in 'packets'? What will energy 'look like' if it was continuous and what is meant by ''only discrete values of energy can exist" ? Please give some examples.
 ANSWER:
ANSWER:
Continuous is what we are used to in Newtonian physics.
Consider a mass m on a spring with spring constant k. What
energy can it have? The energy E of a simple harmonic oscillator
is E=¼kA2 where A is the amplitude of
the oscillation; the frequency of the oscillator is f=[√(k/m)]/(2π).
What restrictions are there on what A can be? In classical
physics there are no restrictions, A, and therefore E, can
be anything you like. This is called a continuous spectrum of
energy. But is this exactly true or simply because we cannot measure A carefully enough to be sure that it really can be anything.
Suppose that only certain values A were allowed in nature and
that they differed by 10-30 m; this would be called a discrete spectrum but there would never be an experiment you could
perform which could observe it. But, maybe if you went to values of m
and k you do not usually experience in everyday life you might see a
discrete spectrum. What Planck hypothesized was that the spectrum of a
simple harmonic oscillator was discrete, not continuous, and the allowed
values of energy were En=nhf where n=0,1,2,3,… and h=6.63x10-34 m2kg/s.
Suppose that we had an oscillator with f=1 s-1, e.g.
m=1 kg, k=4π2 N/m; then
the spacing between allowed energies would be 6.6x10-34 J,
clearly unobservable. But, an electron in an atom might very well have a
frequency of 1016 s-1 and the energy spacings
would be on the order of 10-17 J. This sounds
small, but you could easily measure such energy differences on the
atomic level. Actually, Planck was wrong and the correct spectrum is En=(n+½)hf,
but it was close enough to cause a revolution in physics. It turns out
that any system which is bound has a discrete energy spectrum and any
system which is not bound has a continuous energy spectrum. In everyday
life we do not see discrete spectra because our senses are not sensitive
enough to detect the tiny differences between energies.
 QUESTION:
QUESTION:
I understand that speed is a scalar quantity, but I don't get why. Since speed is written as d/t, and those are two separate measurements, what stops it from being a vector quantity?
 ANSWER:
ANSWER:
There is nothing esoteric here, it is simply a matter of
semantics. The velocity vector is defined to be the rate of change of
the position vector of something. Speed is the word we use to specify
the magnitude of the velocity vector and the magnitude of a vector is
always a scalar. So the reason that speed is a scalar quantity is simply
that it is defined to be. For example, my speed is 60 mph but my
velocity is 60 mph north.
 QUESTION:
QUESTION:
I'm just confused because according to newton's third law of motion, " any action has an opposite but equal reaction", hence forces in nature are balanced, and balanced forces means bodies are at rest, so how come in reality, we can observe motion?
 ANSWER:
ANSWER:
See my FAQ page.
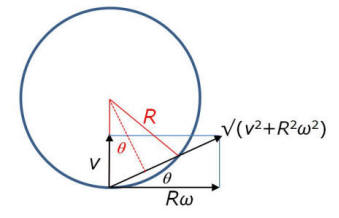
 QUESTION:
QUESTION:
could centrifugal force force actually be used to simulate gravity like in so many sci-fi stories?
one of my favorite sci-fi stories is the Ringworld by Larry Niven. The Ringworld of the title is a giant ring shaped structure the size of earth's orbit. It's centered on a star and has a habitable inside edge, gravity on this inside edge is simulated by the structure spinning fast enough to make objects feel as heavy as they would at 99.2% earth gravity.
If I were stood on a real structure like the Ringworld, and I jumped up in the air, would I fall back down or fly off into space?
 ANSWER:
ANSWER:
Yes, as long as the radius of the ring is large compared to
the size of the objects. In such a scenario, the centripetal
acceleration should be set equal to g, so g=Rω2
where ω is the angular velocity in radians per second. So, the
picture to the right shows the ring as viewed from outside. You now jump
straight up with a speed v. However, note that you also have a
tangential velocity of Rω so your actual velocity is √(v2+R2ω2).
So you see what will happen is that you will go in a straight line with
constant speed (because there are no forces on you) along that velocity
until you again strike the ring; it will seem that you jumped and came
back down. You can calculate the time you were in the air and how high
you went by doing some pretty straightforward geometry/trigonometry.
-
I find the two
angles labeled θ above are the same so sinθ=v/√(v2+R2ω2)
and cosθ=Rω/√(v2+R2ω2).
-
From these you
can find the length of the chord (the length of your flight) C=2Rsinθ=2Rv/√(v2+R2ω2),
-
the height you go
above the surface h=R(1-cosθ)=R(1-Rω/√(v2+R2ω2)),
and
-
the time you are
in the air T=C/√(v2+R2ω2)=2Rv/(v2+R2ω2).
Now, let's compare these with the time and height
on earth. Remember that ω=√(g/R) and I will take
R to be very large compared to compared to v2/g.
So, now I find that
These two approximate results are just the same as
for a projectile launched straight up on earth. Keep in mind, though, that
R must be large. Also, you do not want to jump with a velocity which
has a component parallel to the axis of rotation. If you are too close to
the edge, you will miss the ring when you "fall back".
 QUESTION:
QUESTION:
when someone pushes a box in frictional environment so that the speed of the box is constant, it is usually said in textbooks that the net work done is ZERO, because Fd=-F (frictional)*d. And this seems OK , because of the fact that the box does not accelerate: no energy input. But the box gets hotter and it must be connected with the force applied to the box. So how can net work be zero, shouldn't it be positive?
 ANSWER:
ANSWER:
While it is certainly true that the net work done by you and the
friction is zero and that the change in kinetic energy is zero, this
does not mean that you did zero work. The work which you did gave
energy to the box in the form of heat; this energy, which you added to
the system, cannot be retrieved. An analogous case would be if you
lifted the box at constant speed some height h where you and the
force of gravity (weight) do zero net work. The work which you did gave
energy to the box in the form of potential energy; this energy, which
you added to the system, can be retrieved by simply letting go of the
box which causes that potential energy to be converted into kinetic
energy as the box falls back to the floor. The difference between the
two situations is that weight is a conservative force whereas friction
is not; work done against friction cannot be retrieved as kinetic
energy.
 QUESTION:
QUESTION:
Hello, I have an idea and would like to know if it is possible. If the north poles of two rectangular magnets are secured together and the sides are covered in magnetic shielding so that only the two south poles are exposed, will the geomagnetic field exert a net force on them? This was the premise behind a propulsion scheme that I devised (even though the force produced would be small). This kind of energy-free propulsion should not be possible, but I don't see any reason that would prevent it from working.
 ANSWER:
ANSWER:
You are not going to be able to shield your gizmo and make it
look like a pure north pole. But, you do not have to. If you put a bar
magnet so that its north pole is directly above the earth's magnetic N
pole (which is its geographic S pole) and its S pole is farther away, it
will experience a force away from the earth. The reason is that the
field from a dipole (like the earth) gets weaker as you get farther
away, so the attractive force on your S pole is smaller than the
repulsive force on the N pole. I think if you work out the numbers,
though, you will find it a pretty miniscule force!
 QUESTION:
QUESTION:
How can a photon or any massless particle bounce on things? or how could massless particles like photons be effected by forces of any kind? if it is massless shouldn't it go straight through bodies and not bounce? and what does it even bounce on anyways?
 ANSWER:
ANSWER:
A photon has momentum so it can collide with another particle
and exert forces on the other particle as well as have forces exerted on
it. (That is really a sort of classical way to phrase it, but it gets to
the heart of momentum transfer happening.) Look up Compton scattering,
for example, where photons scatter from electrons. A photon carries
electric and magnetic fields and so it is very interactive with most
things in nature which are composed of electrically charged objects,
either bouncing or getting absorbed.

 QUESTION:
QUESTION:
If you shoot a bullet straight up into the air, its velocity at the very top of the trajectory is zero, even if only for an instant, as its upward velocity slows to nothing before becoming downward velocity. Downward vertical velocity then increases in the earthward direction . Would the velocity ever become dangerous if it landed on a living person? Is the weight of the bullet important? Does the atmosphere restrict the downward velocity?
 ANSWER:
ANSWER:
A falling bullet experiences a downward force of its own
weight and an upward force of air drag. The result of the air drag,
which increases with speed, is to have the falling object eventually
reach a maximum velocity called the terminal velocity which is
determined by its weight and its geometry (which is why you can jump out
of an airplane with a parachute). A .30 caliber bullet weighing about 10
grams has a terminal velocity of about 90 m/s (about 200 mph) and a .50
caliber bullet weighing about 42 grams has a terminal velocity of about
150 m/s (about 335 mph). A bullet traveling 60 m/s (about 130 mph) can
penetrate the skull so, yes, a falling bullet is dangerous. Dozens of
people are killed every year by celebratory gunfire.
 QUESTION:
QUESTION:
I'm trying to explain to student drivers how to avoid going into a skid during bad weather. A common rule of thumb is "skids happen when there is a change in speed or a change in direction."
Ok, so you are going up a hill at a steady 35 mph. When you reach that part of the incline when your automatic would normally downshift to get your rpm's up - you skid.
I know it has something to do with gravity's effect and you are actually accelerating in order to go same speed but somehow I can't seem to explain it right.
 ANSWER:
ANSWER:
The crucial point really is that the coefficient of static
friction is larger than the coefficient of sliding friction. That may be
too technical for your purposes, so let me explain. Static friction is
the frictional force which acts between two objects which in contact but
not sliding; for example, when a car is parked on a hill, the thing
which keeps it there is the frictional force between the tires and the
road and that is static friction. But, as the hill gets steeper, the
friction needed to keep the car from sliding gets bigger and,
eventually, there will not be enough friction and the car will slide
down the hill. But, what happens when the car just starts to
slide? Does the car start creeping slowly down the hill? No, as soon as
it "breaks away" it accelerates down the hill. The reason is that the
sliding friction is less than the static friction. The same is true when
the car is moving because the wheels are not slipping and therefore
static friction is operative. If you are moving with constant speed on a
straight, level road, almost no friction is needed to keep going. But,
when you accelerate you need more static friction from the tires (just
like you need more static friction on a steeper hill) and if you try to
accelerate too much your wheels will spin (just like the car will slide
down the hill). Or, if you brake you need more static friction from the
tires (just like you need more static friction on a steeper hill) and if
you try to brake too rapidly your wheels will skid (just like the car
will slide down the hill). You probably tell your students that they can
stop quicker if they do not slam on the brakes and skid; again, the
smaller sliding friction is why and that is why anti-lock brakes are
such a good safety feature. Turning a curve also requires static
friction because a turning car is actually accelerating even if the
speed is constant because the dirction of the velocity is changing; on a
very icy road where you can get almost no static friction, when you
steer into a curve nothing will happen and you will just skid straight
forward off the road. Your example about going up a slippery slope and
downshifting is more or the less the same as braking gently, trying to
get more static friction. Essentially, trying to keep a car going up the
hill at a constant speed is exactly the same as parking on the hill�the
static friction required is the same and if the hill is slippery and
steep enough, you will be able to neither park nor go up with constant
speed. So, the downshifting has the same effect as accelerating, trying
to get more static friction. Even if you do not downshift, to keep going
up with constant speed would require that you give the car more gas than
on a level road.
 QUESTION:
QUESTION:
Balancing a glass on knives how does it work?
The video.
 ANSWER:
ANSWER:
It seems to me that they show you how to do it in the video.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
i'M
sorry I mean why does this happen? How come the three knives hold the glass?

 ANSWER:
ANSWER:
Examine each knife. Each has a force A up on
its handle from a glass; each has a force B up at the end of
its blade from one of the other three knives; each has a force C
down from the third knife; each knife has a force of its own weight
W down at the center of mass of the knife (where you could
balance it without any forces but the weight acting on it). On that knife,
the sum of the forces is zero, A+B-C-W=0. On that knife, the sum of
the torques about any axis is zero; for example, about the glass end the
where A is applied, B(d1+d2)-Cd1-Wd3=0.
These conditions are satisfied and the knives are all in equilibrium. There
is another interesting thing you can note: the force C on this
knife is the force one of its neighbors exerts down on it with the end of
its blade; but, by Newton's third law, the forces forces these two knives
exert on each other are equal and opposite. It follows, therefore, that C=B since the knives are symmetrically arranged and all three must have
the same forces on them. You can also see that the three glasses must hold
up the total weight of the three knives, so 3A=3W, A=W.
If you solve for these forces you will find A=W
and C=B=W(d2/d3). Putting the
beer glass on top simply increases the forces B, C,
and A but the knives remain in equilibrium. Is this what you
were looking for?
 QUESTION:
QUESTION:
With all this future talk about harvesting asteroids, I have an interesting thought experiment... how would the force of gravity shared by the sun and the earth (aka our orbit) be affected by an increase in the earths mass. Or, would the amount of asteroid mass be insignificant in that equation?
 ANSWER:
ANSWER:
The earth's orbit, both shape and period, are independent of
its mass (unless the mass of the earth became comparable to the mass of the
sun which will certainly not happen). But, your last sentence certainly hits
the nail on the head that the added mass would be insignificant compared to the
mass of the earth. If the mass of the earth increased signficantly, though,
the period of the moon would change.
 QUESTION:
QUESTION:
I have always wondered why the "speed of light" is regarded as a constant when in a vacuum. If light has a finite speed in a vacuum, then the following questions puzzle me:
1. Does light accelerate?
2. what is its rate of acceleration?
3. If so, why is there a finite speed in a vacuum?
 ANSWER:
ANSWER:
To answer your first question, why is the speed of light a
constant in vacuum, see my FAQ page.
The answers to your questions:
-
Light can accelerate only by changing its
direction, not its speed.
-
The rate of acceleration bending light depends
on the gravitational field in the vicinity; this is called gravitational
lensing.
-
Again, see the
FAQ page. If you want to know why
it has the value it has, 3x108 m/s, see another question on my
FAQ page.
Note that it is important that you understand that
"accelerate" does not have to mean change of speed, it can also mean change
of direction.
 QUESTION::
QUESTION::
why is that during daytime when you turn on the headlights if your car the object ahead of you doesnt appearr to be brigther?
 ANSWER:
ANSWER:
Imagine you are sitting in a quiet room and whisper to the
person next to you. She can hear you. Now imagine that a jet airplane is
roaring right over your house. If you whisper, you will not be heard. The
headlights are a whisper compared to the intensity of sunlight.
 QUESTION:
QUESTION:
I'm very confused about work. Let's say that I'm lifting a 10 kg backpack up 50 meters. That means that the work that I just did is 10 times 9.8 (acceleration of gravity) times 50 since W=Fd and F=ma. So if I did that work, then that means that I applied 10 times 9.8 Newtons of force. That is equal to the force that gravity applies to the backpack. Therefore, there would be no acceleration. But then, another definition of work as you know is the change of kinetic energy. But if there is no acceleration, then there is no kinetic energy. Which leads to the conclusion of no work. What am I doing wrong here? I'm very confused.
 ANSWER:
ANSWER:
You are not doing anything wrong, it is just that you have
specify who does the work. When you carry the pack up the mountain, you do
4900 J of work. During that same time, the earth is doing -4900 J of
work, negative because the displacement (up) is opposite the force (weight,
down). You and the earth together do zero net work, so the kinetic energy
does not change. When you equate change in kinetic energy to work done, you
must include the total work done.
 QUESTION:
QUESTION:
"A tube in the shape of a rectangle with rounded corners is placed in a vertical plane. You introduce two ball bearings at the upper right-hand corner. One travels by path AB and the other travels by path CD. Which will arrive first at the lower left-corner?"
My problem is with the velocity of the ball at the end of traveling down the first side, whether it be A or C. The problem states 'rounded corners'. Surely the ball does not come to a stop -i.e. zero velocity, as it turns the corner. So I would guess that there is a significant velocity after 'rounding' the corner and hence must be accounted for.
 ANSWER:
ANSWER:
This is a problem out of Halliday and Resnick, Chapter 3 on
kinematics. I have been assured that it not homework, rather someone
brushing up on introductory physics. I must admit that I am a little puzzled
by it because, although I can solve the problem analytically as a function
of the sides A and C and the angle θ which C makes with the
vertical, none of these is given; this means to me that there must be some
obvious qualitative reasoning for this picture which does not require any
details. In this picture, the ball going down C will have a much bigger
acceleration than the ball going down A because it is steeper; since C is
shorter, that ball will arrive at its turn earlier than the other ball.
Also, because the first corner is lower along C than along A, the C ball
will be going faster when it gets to its corner than the A ball will be. So,
the C ball turns the corner earlier and with a higher speed. The C ball
wins. That's the best I can do with qualitative reasoning. (I would be glad
to have anybody write in with a better explanation.) However, my curiosity
led me to solve the problem analytically so I could examine all the
possibilities. I will not give the anaytical solutions for both of the two
paths since they are a little messy, but they depend on A, C, and θ;
click here to see these solutions. Plotted below are the times as a function of
θ for 00-900.
The case most closely resembling the given problem is where A=2C with θ≈300;
The C ball is the clear winner as speculated above. One
interesting thing to note is that when θ=450, the balls
take the same time regardless of the lengths of the sides. This is easy to
understand because both balls have identical accelerations of 0.707g
the whole time. And, the ball starting on the steeper slope always wins the
race, regardless of the lengths or the angle θ. Note also that as
θ―>00 the time for A ―>∞, and as
θ―>900
the time for C ―>∞. This is also easy to understand because a
ball in a horizontal tube will not move at all.
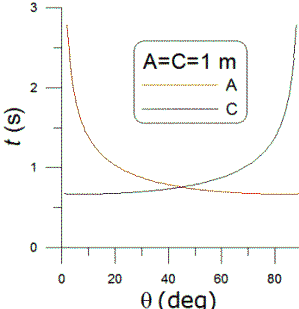
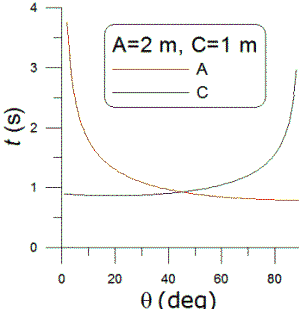
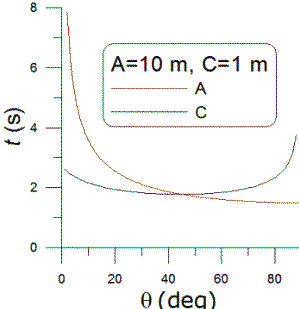
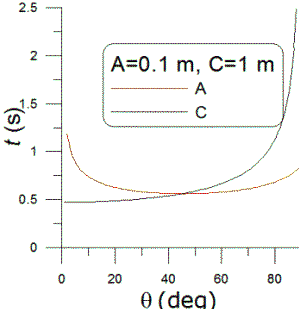

 QUESTION:
QUESTION:
I'm hoping you can settle a bet between my father and myself. We are
both movie buffs, and work together. While working we discussed the
Ah-nuld movie "Eraser". I'm going to make the assumption you have never
seen the movie which revolves heavily around the manufacture of
man-portable super-railguns that fire aluminum rounds at 'close to the
speed of light'. Being firearms enthusists as well, we discussed the
flaws in their idea (beyond the fact no technology in the near future
would allow such a weapon as the one depicted to be made, let alone one
man-portable.) Where we came to a disagreement was why for other reasons
it would be useless. While we agree that the mooks Ah-nuld tears through
as he does in every movie would be out of luck. In practical situations
the weapon would be useless but we disagree why. My father believes that
a 5.56mm / 0.00401753242 kg bullet (our assumptions) traveling 80% of c
would immediately flatten out and quickly lose all of its kinetic energy
due to its low mass and aluminin's relatively soft nature upon striking
anything solid such as a door, or brick. I say a round with the same
dimensions would explode on contact with something solid (again like a
brick) as the work-heating would vaporize a piece of aluminimum with
that mass. If it could even get there without being melted by
atmospheric friction. As I've submitted questions to you before we
decided we would --drum roll--- ASK THE PHYSICIST!!! Are either of us
correct? The loser has to buy the next Pizza we order.
 ANSWER:
ANSWER:
Neither of you is addressing the real issue here—a 4 gram
bullet traveling at 80% the speed of light has an almost incomprensible
amount of energy. So, saying that this weapon would "be useless" is way off
the mark. Saying that it is impossible to make such a weapon is a different
issue which I will address after talking about what such a speedy bullet
would do. You are probably not interested in the details, so I will just
give you the kinetic energy such a bullet would have—about 5x1014
Joules. To put that in perspective, if you took that energy and delivered it
to the power grid over a period of a day, this would be the equivalent of a
6 gigawatt (6x109 watts=6 billion Joules per second) power
station. The largest power station in the US has a power output of about 4
gigawatts. Or, the energy of the Nagasaki atomic bomb was about 1014
Joules, 1/5 of the energy of your 4 gram bullet. So to argue whether the
bullet's flattening or exploding is the reason it would not do much damage
sort of misses the point, don't you think?! If the bullet takes 10 seconds
to deliver its energy to whatever can take it, you are still talking about
the energy of 5 WWII-era atomic bombs being delivered. I would not want to
be within 50 miles of that. Finally, it means that the "gun" has to deliver
all that energy in an unimaginably short amount of time (I presume that
since, if it is "man-portable", the gun must be no more than a few feet
long). I figure that a force on the bullet of more than 2 million pounds
would be required during the time it was in the gun; do you think an
aluminum bullet could withstand such a force? And, Newton's third law says
that, if the gun exerts that force on the bullet, the bullet would exert
that force on the gun. Imagine the recoil! This is such a ridiculous
scenario, I don't think we even need to beat a dead horse and talk about
what air friction would cause to happen as it flew to the target.
-
To see
questions and answers from longer ago, link
here.