I will do the time-independent Schrödinger equation because it is easiest to understand without much mathematics. Also, I will do the one-dimensional version; think of a bead moving on a wire or perhaps a mass attached to a spring and bouncing back and forth.

First, do classical physics: total energy E is the sum of kinetic energy T (energy by virtue of motion) plus potential energy V(x) (energy by virtue of position in some force field), . The kinetic energy is where m is tha mass of the object and v is its speed. But, since linear momentum p is , kinetic energy is often written as , so . Schrödinger’s equation is nothing more than the quantum mechanical equivalent of this almost intuitive (the total is the sum of its parts) energy equation.

So, what is different about quantum mechanics? It turns out that some quantities in nature must be treated as mathematical operators, not as just simple numbers like they are in classical mechanics. This is the case for linear momentum which becomes where , the imaginary unit, where h is a fundamental constant called Planck’s constant, and is the derivative with respect to x. If you have never studied calculus, a derivative is an operator which, when it operates on a mathematical function, tells you how fast that function is changing as x changes. Planck’s constant is an extremely small number which is why quantum mechanics is not noticeable except for very tiny systems (think atoms, nuclei, etc.).

Now, of necessity, things get a little more mathematical; but if you get a little lost here, just carry on. We still might want to know what the linear momentum is, not just what the operator associated with it is. To do this we must introduce what is called an eigenvalue equation which is of the form OΦ(x)=OΦ(x). O is the operator, Φ(x) is called the eigenfunction, and O is the called the eigenvalue. The eigenfunction contains the information about what the system we are interested in is, and the eigenvalue is what the observable quantity associated with the operator is. For example, if it is linear momentum we are interested in, then where p is the value of the momentum you would measure.

Back to Schrödinger’s equation: we still use but now . ( means the derivative of the derivative, but that is not so important, just math.) So now the total energy of a system is an operator, not a number. This operator is called the Hamiltonian, . To find the energy of a system, therefore, there must be an eigenvalue equation; this is Schrödinger’s equation . The eigenfunction is called the wavefunction and has a very special meaning. It has no particular physical meaning on its own but, when squared, it becomes the probability density function. This means that is the probability of finding the particle between the positions x and x+dx where dx is some very small change in x. Of course, if is to have this meaning, the sum of all probabilities over all space must add up to 1 ( the particle has to be somewhere).

From here on it is a matter of applying this equation to a particular system to find out what energies will satisfy the equation. A one-dimensional example is a mass on a spring. When you put in the appropriate potential energy function you find that the spring cannot have just any old energy, there are only certain energies which will satisfy the Schrödinger equation; these are where n is any positive integer or zero and f is the frequency which the particular spring oscillates with. Another example is an atom. Here, of course, we have a three-dimensional problem and have to use a three-dimensional Schrödinger equation which would have the form . 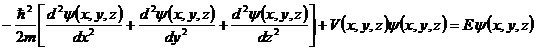What you find is still that an atom can only exist in certain energy states, not any old energy you might want.